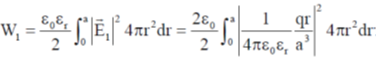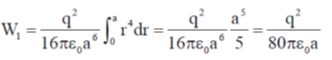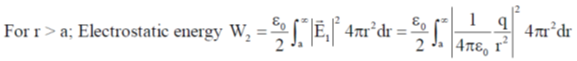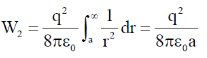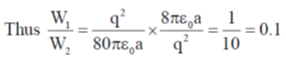1. The equation 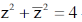in the complex plane (where 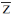is the complex conjugate of z) represents (a) Ellipse

(b) Hyperbola

(c) Circle of radius 2

(d) Circle of radius 4

Ans. (b)

Sol.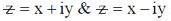

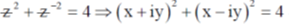
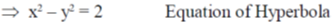
2. A rocket (S') moves at a speed 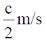along the positive x-axis, where c is the speed of light. When it crosses the origin, the clocks attached to the rocket and the one with a stationary observer (S) located at x = 0 are both set to zero. If S observes an event at (x, t), the same event occurs in the S' frame at

(a)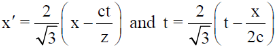

(b)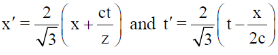

(c)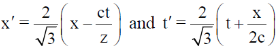

(d)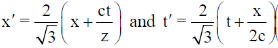

Ans. (a)

Sol. From the question one Rocket S' moving with speed of C/2 and one observer is standing x = 0. For point P the coordinate at S frame is (x, y) and the coordinate at S' frame is (x', y')

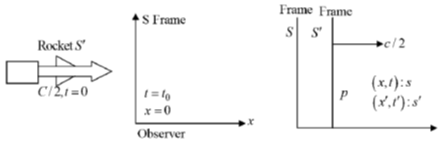
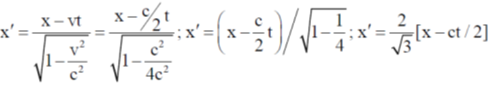
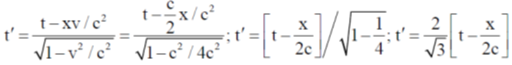
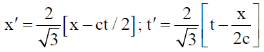
Correct option is (a)

3. Consider a classical ideal gas of N molecules in equilibrium at temperature T. Each molecule has two energy levels, . The mean energy of the gas is

(a) 0

(b)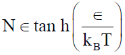

(c)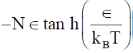

(d)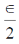

Ans. (c)

Sol. The partition function for a single gas molecule is

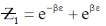
Mean energy per particle,

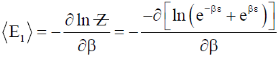
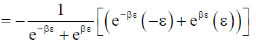
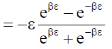
the mean energy is

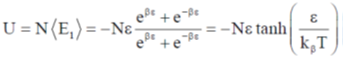
4.

(a)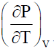

(b)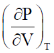

(c)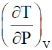

(d)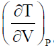

Ans. (a)

Sol. Given

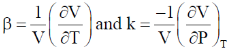
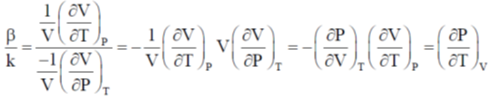
Here, in the last step we made use of reciprocity theorem i.e

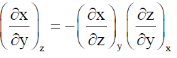
5. The resultant of the binary subtraction 1110101 – 0011110 is

(a) 1001111

(b) 1010111

(c) 1010011

(d) 1010001

Ans. (b)

Sol. 2s compliment of 0011110

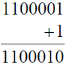
Thus 1110101 – 0011110 is

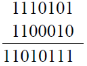
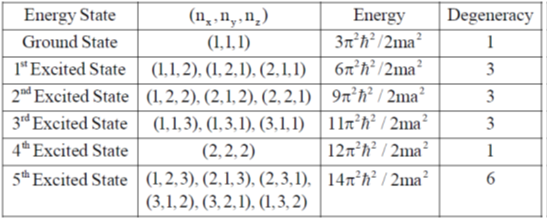
6. Consider a particle trapped in a three-dimensional potential well such that U(x, y, z) = 0 for 0 < x style="text-decoration: underline;">< a, 0 < y style="text-decoration: underline;">< a, 0 < z < a and U(x, y, z) = 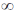everywhere else. The degeneracy of the 5^th excited state is

(a) 1

(b) 3

(c) 6

(d) 9

Ans. (c)

Sol. Energy for 3d Potential well is

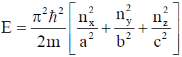
From question a = b = c = a so,

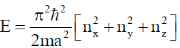
7. A particle of mass m and angular momentum L moves in space where its potential energy is

U(r) = kr² (k > 0) and r is the radial coordinate.

If the particle moves in a circular orbit, then the radius of the orbit is

(a)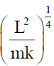

(b)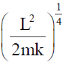

(c)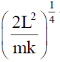

(d)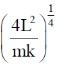

Ans. (b)

Sol. Let the velocity of the particle is v and angular momentum L.

Method 1:- We have

U(r) = kr²

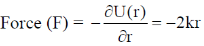
We know that centripetal force

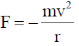
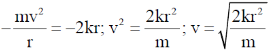
angular momentum L = mvr

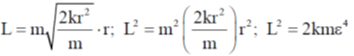
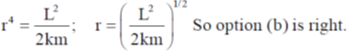
Method:-2

We know that the effective potential of the system is

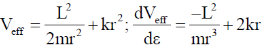
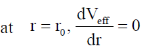
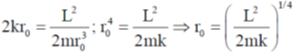
8. Consider a two-dimensional force field

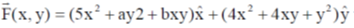
If the force field is conservative, then the values of a and b are

(a) a = 2 and b = 4

(b) a = 2 and b = 8

(c) a = 4 and b = 2

(d) a = 8 and b = 2

Ans. (b)

Sol.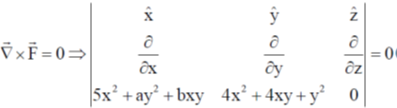

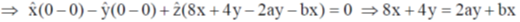
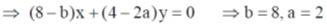
9. Consider an electrostatic field 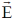in a region of space. Identify the INCORRECT statement.

(a) The work done in moving a charge in a closed path inside the region is zero

(b) The curl of is zero

(c) The field can be expressed as the gradient of a scalar potential

(d) The potential difference between any two points in the region is always zero

Ans. (d)

Sol. Correct option is (d)

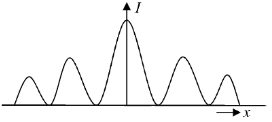
10. Which one of the following figures correctly depicts the intensity distribution for Fraunhofer diffraction due to a single slit? Here, x denotes the distance from the centre of the central fringe and I denotes the intensity.

(a)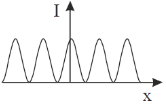

(b)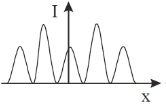

(c)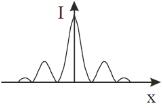

(d)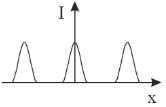

Ans. (c)

Sol.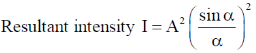

11. The function f(x) = e^{sin x} is expanded as a Taylor series in x, around x = 0, in the form 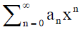. The value of a₀ + a₁ + a₂ is

(a) 0

(b)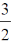

(c)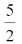

(d) 5

Ans. (c)

Sol. f(x) = e^{sin x}

Taylor's series around x = 0

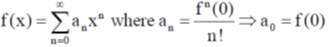
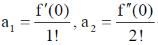
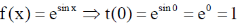
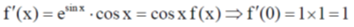
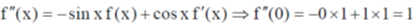
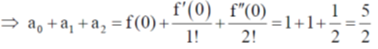
12.

(a) 0

(b)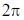

(c)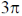

(d)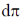

Ans. (b)

Sol.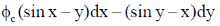

Using Green's theorem for a plane

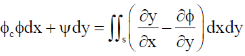
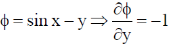
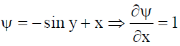
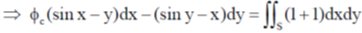
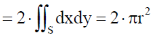
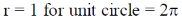
13.

(a) 1 – 2e^–2

(b) 1 – 2e^–1

(c) 1 – e^–1

(d) 2 – 2e^–1

Ans. (c)

Sol.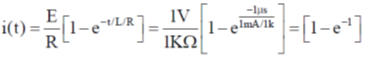

14.

(a)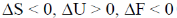

(b)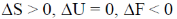

(c)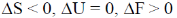

(d)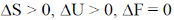

Ans. (b)

Sol. For an Ideal gas undergoing isothermal expression

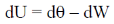
dU = 0

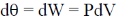
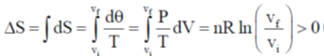
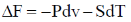
dT = 0, dV > 0

15.

(a)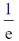

(b)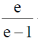

(c)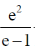

(d)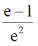

Ans. (d)

Sol.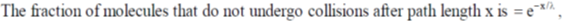

Therefore, the fraction of molecules with free path length between

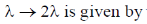
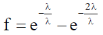
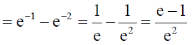
16. Consider a quantum particle trapped in a one-dimensional potential well in the region [–L/2 < x < L/2], with infinitely high barriers at x = – L/2 and x = L/2. The stationary wave function for the ground state is 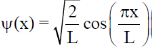. The uncertainties in momentum and position satisfy

(a)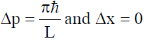

(b)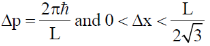

(c)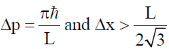

(d)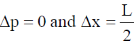

Ans. (b)

Sol.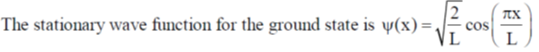

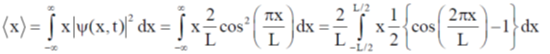
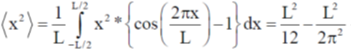
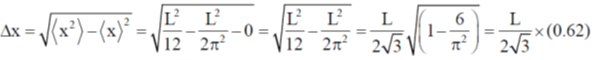
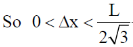
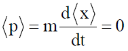
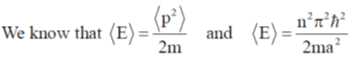
Put the n = 1 and a = L/2

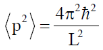
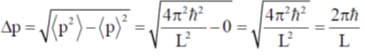
17.

(a)

(b)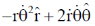

(c)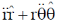

(d)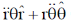

Ans. (b)

Sol.

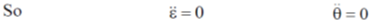
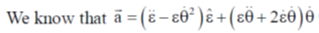
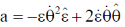
Correct option is (b)

18. A planet of mass m moves in an elliptical orbit. Its maximum and minimum distances from the Sun are R and r, respectively. Let G denote the universal gravitational constant, and M the mass of the Sun. Assuming M >> m, the angular momentum of the planet with respect to the center of the Sun is

(a)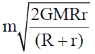

(b)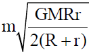

(c)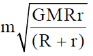

(d)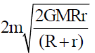

Ans. (a)

Sol. Assume Sun is at the center of the elliptical orbit.

Consider conservation of Energy

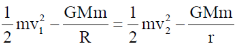
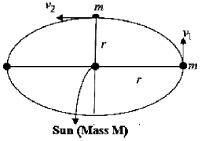
Conservation of angular momentum

mrv₂ = mv₁R

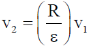
From Eq (1)

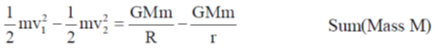
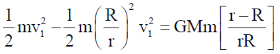
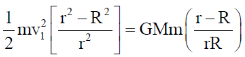
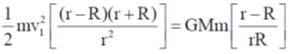
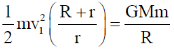
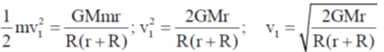
L = mv₁R

Correct option is (a)

19. Consider a conical region of height h and base radius R with its vertex at the origin. Let the outward normal to its base be along the positive x-axis, as shown in the figure. A uniform magnetic field, 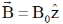exists everywhere. Then the magnetic flux through the base 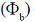and that through the curved surface of the con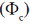e are

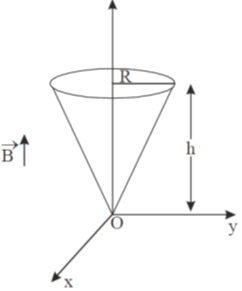
(a)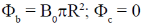

(b)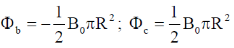

(c)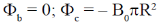

(d)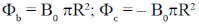

Ans. (d)

Sol.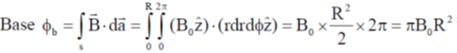

20.

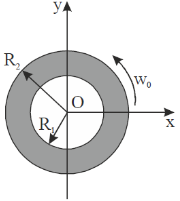
(a)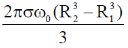

(b)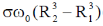

(c)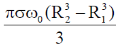

(d)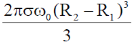

Ans. (a)

Sol.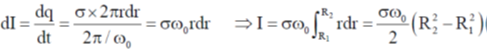

21.

(a)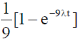

(b)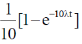

(c)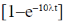

(d)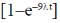

Ans. (a)

Sol. We know that

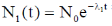
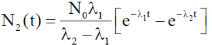
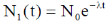
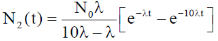
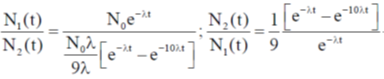
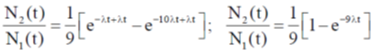
Correct option is (a)

22.

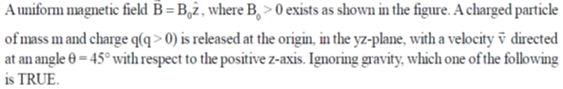
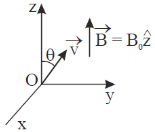
(a)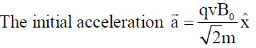

(b)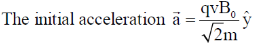

(c) The particle moves in a circular path

(d) The particle continues in a straight line with constant speed

Ans. (a)

Sol.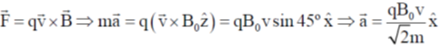

23. For an ideal intrinsic semiconductor, the Fermi energy at 0 K

(a) lies at the top of the valence band

(b) lies at the bottom of the conduction band

(c) lies at the center of the band gap

(d) lies midway between center of the band gap and bottom of the conduction band

Ans. (c)

Sol.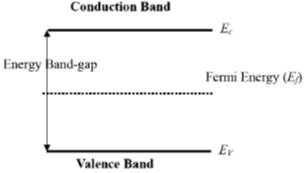

24. A circular loop of wire with radius R is centered at the origin of the xy-plane. The magnetic field at a point within the loop is, 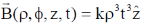, where k is a positive constant of appropriate dimensions. Neglecting the effects of any current induced emf in the loop, the magnitude of the induced emf in the loop at time t is

(a)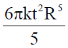

(b)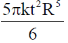

(c)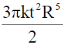

(d)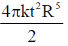

Ans. (a)

Sol.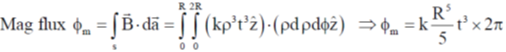

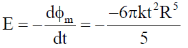
25.

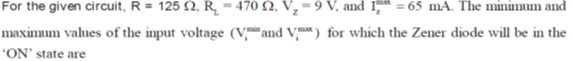
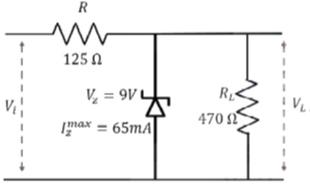
(a)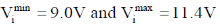

(b)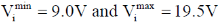

(c)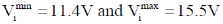

(d)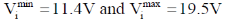

Ans. (d)

Sol.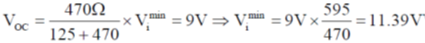

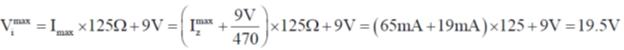
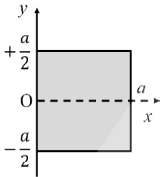
26. A square laminar sheet with side a and mass M, has mass per unit area given by 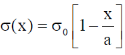, (see figure). Moment of inertia of the sheet about y-axis is

(a)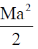

(b)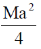

(c)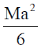

(d)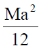

Ans. (c)

Sol. We have mass per unit area given by

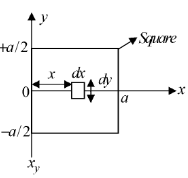
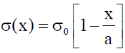
So mass of square linear sheet

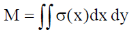
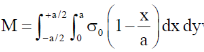
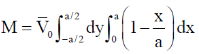
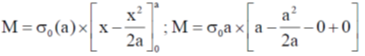
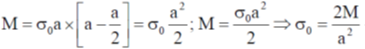
The moment of Inertia with y-axis

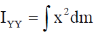
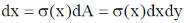
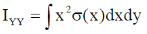
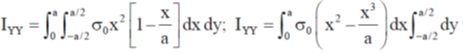
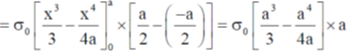
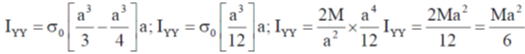
Correct option is (c)

27.

(a)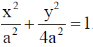

(b) x² + y² = 1

(c)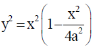

(d)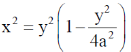

Ans. (d)

Sol. From question

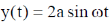
From Eq. (1), we have

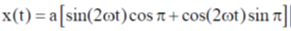
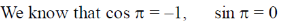
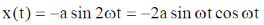
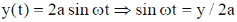
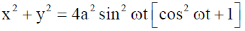
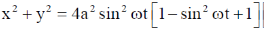
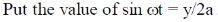
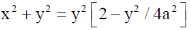
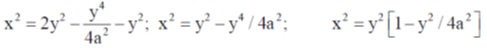
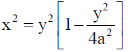
28. For a certain thermodynamic system, the internal energy U = PV and P is proportional to T². The entropy of the system is proportional to

(a) UV

(b)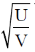

(c)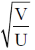

(d)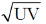

Ans. (d)

Sol. U = PV, P = KT²

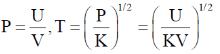
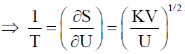
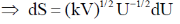
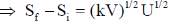
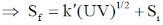
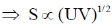
S_i being constant.

29. The dispersion relation for certain type of waves is given by 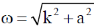, where k is the wave vector and a is a constant. Which one of the following sketches represents v_g, the group velocity?

(a)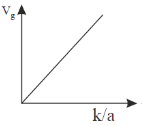

(b)

(c)

(d)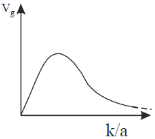

Ans. (b)

Sol. From question, we have

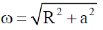
We know that

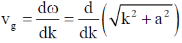
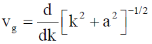
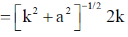
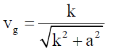
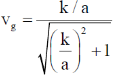
Let k/a = y

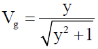
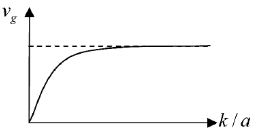
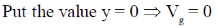
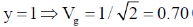
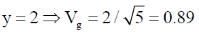
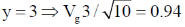
For higher values of y the value of V_g tends to 1.

30. Consider a binary number with m digits, where m is an even number. This binary number has alternating 1's and 0's, with digit 1 in the highest place value. The decimal equivalent of this binary number is

(a) 2^m – 1

(b)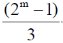

(c)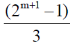

(d)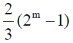

Ans. (d)

Sol. (10)₂ = (2)₁₀; (1010)₂ = (10)₁₀; (101010)₂ = (42)₁₀ ...........

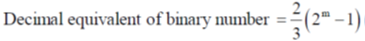
For m = 2; Decimal equivalent = 2

For m = 4; Decimal equivalent = 10

For m = 6; Decimal equivalent = 42

31.

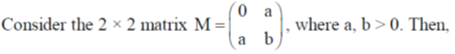
(a) M is a real symmetric matrix

(b) One of the eigenvalues of M is greater than b

(c) One of the eigenvalues of M is negative

(d) Product of eigenvalues of M is b

Ans. (a, b, c)

Sol.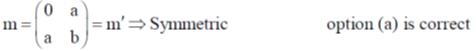

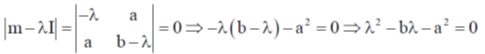
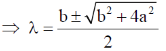
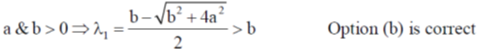
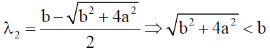
= (–)ve Option (c) is correct

32. In the Compton scattering of electrons, by photons incident with wavelength ,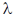

(a)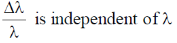

(b)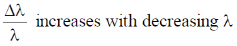

(c) there is no change in photon's wavelength for all angles of deflection of the photon

(d)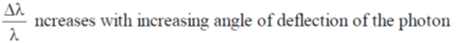

Ans. (b, d)

Sol. We know that

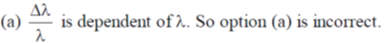
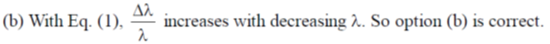
33.

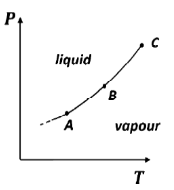
(a)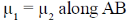

(b) v₁ = v₂ along AB

(c) s₁ = s₂ along AB

(d) v₁ = v₂ along C

Ans. (a, d)

Sol. Along equilibrium line AB

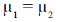
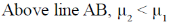
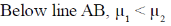
At critical point (and above) the distinction between liquid and vapour phase disappear, as a result v₁ = v₂ at point C.

34. A particle is executing simple harmonic motion with time period T. Let x, v and a denote the displacement, velocity and acceleration of the particle, respectively, at time t. Then,

(a)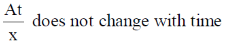

(b)

(c) x and y are related by an equation of a straight line

(d) v and a are related by an equation of an ellipse

Ans. (a, d)

Sol. We know that simple harmonic motion of a particle, the variation of the displacement the velocity and the acieration is sinusoidal with time. So

Option (a):-

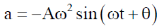
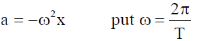
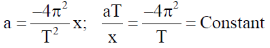
This equation is independent of tine (t). So option (a) is correct.

Option (b):-

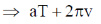
Put the values of a and v from Eq. (2) and (3)

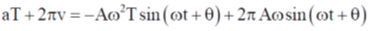
This equation has variation of t. So option (b) is incorrect.

Option (c):-

From Eq. (1) and (2)

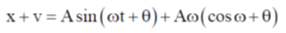
This equation has variation of t. So option (c) is incorrect.

Option (d):-

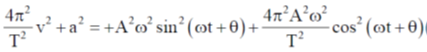
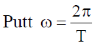
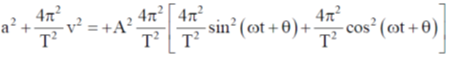
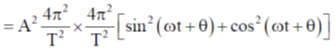
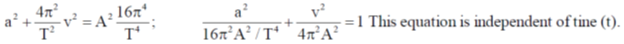
So option (d) is correct.

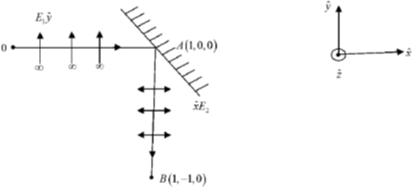
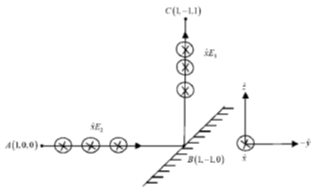
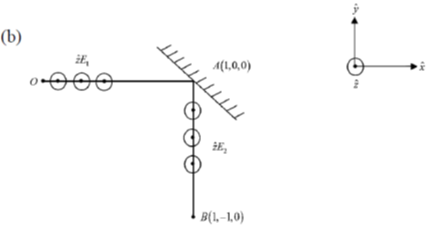
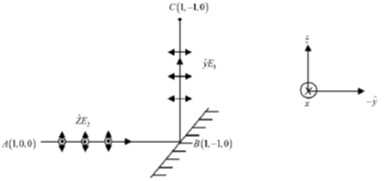
35. A linearly polarized light beam travels from origin to point A (1, 0, 0). At the point A, the light is reflected by a mirror towards point B (1, –1, 0). A second mirror located at point B then reflects the light towards point C (1, –1, 1). Let 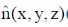represent the direction of polarization of light at (x, y, z).

(a)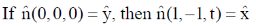

(b)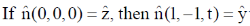

(c)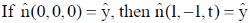

(d)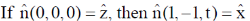

Ans. (a, b)

Sol. If plane polarized light is incident on a mirror at some oblique angle, then only that component of electric field will propagate after reflection, whose direction is perpendicular to the propagation vector.

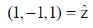
36.

(a)

(b)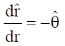

(c)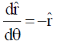

(d)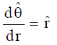

Ans. (a, c)

Sol.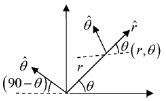

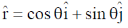
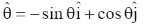
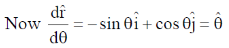
option (a) is correct

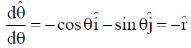
option (c) is correct

37.

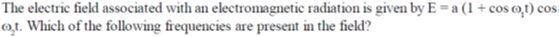
(a)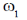

(b)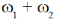

(c)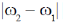

(d)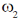

Ans. (b, c, d)

Sol.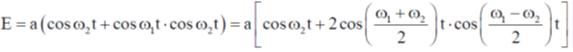

38. A string of length L is stretched between two points x = 0 and x = L and the endpoints are rigidly clamped. Which of the following can represent the displacement of the string from the equilibrium position?

(a)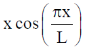

(b)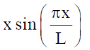

(c)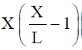

(d)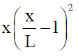

Ans. (b, c, d)

Sol. As string is clamped at x = 0 and x = L, so following two condition should be satisfied:

(i) Displacement y = 0 at x = 0

(ii) Displacement y = a at x = L

Above mentioned conditions are satisfied in case of options (b), (c) and (d).

39.

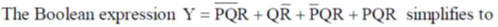
(a)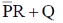

(b)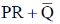

(c) P + R

(d) Q + R

Ans. (d)

Sol.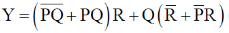

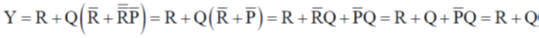
40. For an n-type silicon, an extrinsic semiconductor, the natural logarithm of normalized conductivity 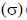is plotted as a function of inverse temperature. Temperature interval-I corresponds to the intrinsic regime, interval-II corresponds to saturation regime and interval-III corresponds to the freeze-out regime, respectively. Then

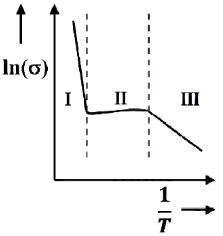
(a) The magnitude of the slope of the curve in the temperature interval-I is proportional to the band gap, E_g

(b) the magnitude of the slope of the curve in the temperature interval-III is proportional to the ionization energy of the donor, E_d

(c) in the temperature interval-II, the carrier density in the conduction band is equal to the density of donors

(d) in the temperature interval-III, all the donor levels are ionized

Ans. (a, b, c)

Sol. Correct options are (a, b, c)

41.

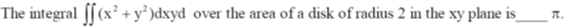
Ans. (8)

Sol.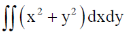

in polar coordinate

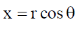
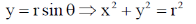
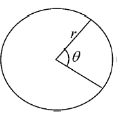
for dxdy = Jacobean

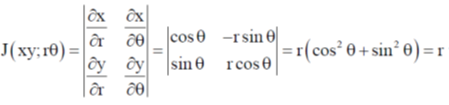
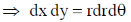
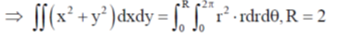
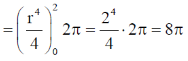
42.

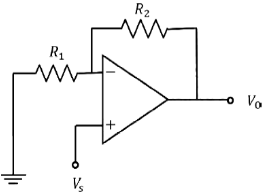
Ans. (5)

Sol.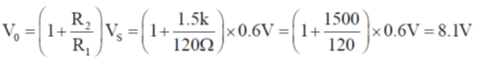

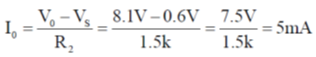
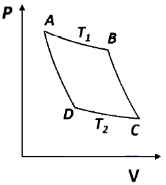
43. For an ideal gas, AB and CD are two isothermals at temperatures T₁ and T₂ (T₁ > T₂), respectively. AD and BC represent two adiabatic paths as shown in figure. Let V_A, V_B and V_D be the volumes of the gas at A, B, C and D respectively. If , _________.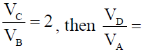

Ans. (2)

Sol. Point B and C are connected aria adiabatic process

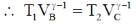
points A&D are also connected uia adiabatic process

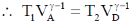
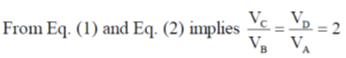
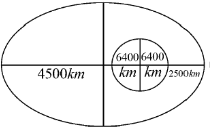
44. A satellite is revolving around the Earth in a closed orbit. The height of the satellite above Earth's surface at perigee and apogee are 2500 km and 4500 km, respectively. Consider the radius of the Earth to be 6500 km. The eccentricity of the satellite's orbit is ____ (Round off to 1 decimal place).

Ans. (0.1)

Sol. r_max = 4500 + 6400 = 10400 km

r_min = 2500 + 6400 = 8900 km

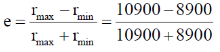
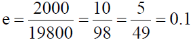
45. Three masses m₁ = 1, m₂ = 2 and m₃ = 3 are located on the x-axis such that their center of mass is at x = 1 . Another mass m₄ = 4 is placed at x₀ and the new center of mass is at x = 3. The value of x₀ is _____.

Ans. (6)

Sol.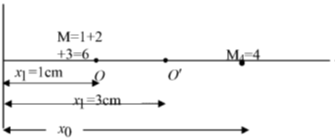

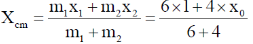
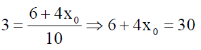
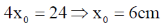
46. A normal human eye can distinguish two objects separated by 0.35 m when viewed from a distance of 1.0 km. The angular resolution of eye is ________seconds (Round off to the nearest integer).

Ans. (71 to 73)

Sol. We know that

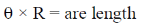
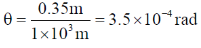
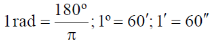
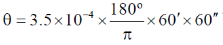
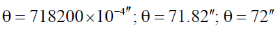
47. A rod with a proper length of 3 m moves along x-axis, making an angle of 30° with respect to the . If its speed is 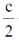, where c is the speed of light, the change in length due to Lorentz contraction is ____m (Round off to 2 decimal places).

[Use c = 3 × 10⁸ m/s]

Ans. (0.29 to 0.31)

Sol. Frame S' is moving with the speed C/2 and the length of the rod is 3m in the frame of S'. So

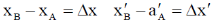
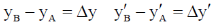
We know that

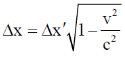
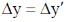
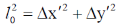
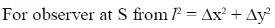
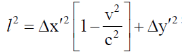
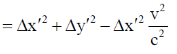
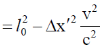
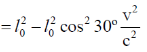
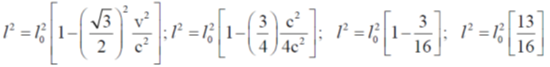
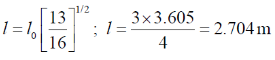
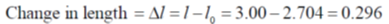
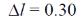
48. Consider the Bohr model of hydrogen atom. The speed of an electron in the second orbit n = 2) is ______× 10⁶ m/s (Round off to 2 decimal places).

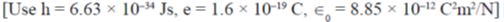
Ans. (1.08 to 1.12)

Sol.

For n = 2

49.

Ans. (2)

Sol.

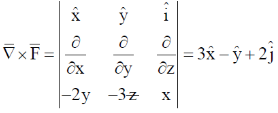
Vector field circularly over a plane for line integral of a vector for field using stake's theorem

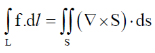
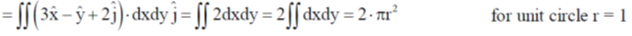
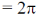
50.

Ans. (0.57 to 0.61)

Sol. Correct answer is (0.57 to 0.61)

51. Consider the second order ordinary differential equation, y'' + 4y' + 5y = 0. If y(0) = 0 and y'(0) = 1, then the value of 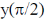is __________ (Round off to 3 decimal places).

Ans. (0.041 to 0.045)

Sol. y'' + 4y' + 5y = 0

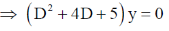
Auxiliary Equation

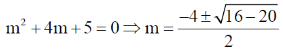
= –2 ±i

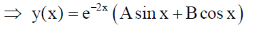
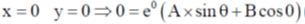
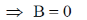
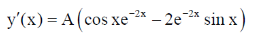
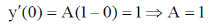
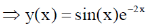
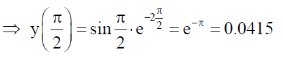
52. A box contains a mixture of two different ideal monoatomic gases, 1 and 2, in equilibrium at temperature T. Both gases are present in equal proportions. The atomic mass for gas 1 is m, while the same for gas 2 is 2m . If the rms speed of a gas molecule selected at random is 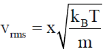then x is __________

(Round off to 2 decimal places).

Ans. (1.49 to 1.51)

Sol.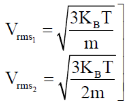

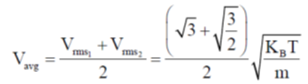
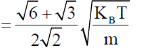
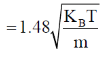
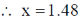
NOTE: The value obtained does not match with given range i.e 1.49-1.51.

53. A hot body with constant heat capacity 800 J/K at temperature 925 K is dropped gently into a vessel containing 1 kg of water at temperature 300 K and the combined system is allowed to reach equilibrium. The change in the total entropy 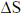is _________ J/K (Round off to 1 decimal place).

[Take the specific heat capacity of water to be 4200 4200J/kg K. Neglect any loss of heat to the vessel and air and change in the volume of water.]

Ans. (537.5 to 537.7)

Sol. C₁ = 800 J/K, T₁ = 925 K

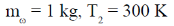
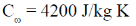
Let T_f be the final temperature

Heat lost = Heat gained

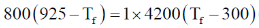
7400 – 8T_f = 42T_f – 12600

50T_f = 7400 + 12600 = 20,000

T_f = 400 K

Entropy change of block

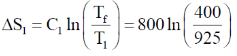
Entropy change of water

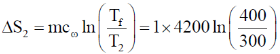
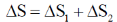
= –670.663352 + 1208.2647

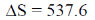
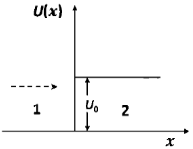
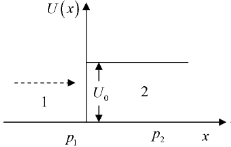
54. Consider an electron with mass m and energy E moving along the x-axis towards a finite step potential of height U₀ as shown in the figure. In region 1 x < 0), the momentum of the electron is 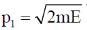. The reflection coefficient at the barrier 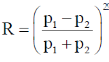, where p₂ is the momentum in region 2. If, in the limit is given by 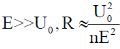, then the integer n is ___.

Ans. (16)

Sol.

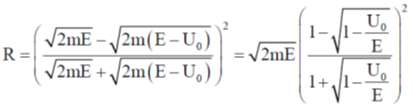
Form question E >> U₀, U₀/E << 1

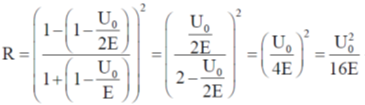
n = 16

55. A current density for a fluid flow is given by,

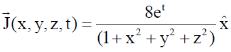
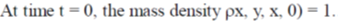
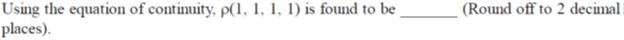
Ans. (2.70 to 2.74)

Sol. Correct answer is (2.70 to 2.74)

56.

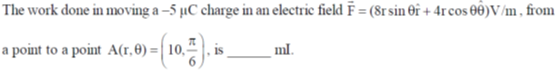
Ans. (1)

Sol.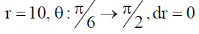

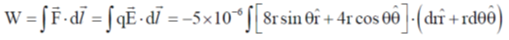
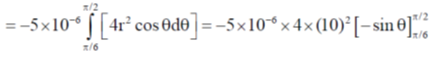
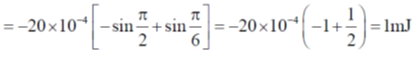
57. A pipe of 1 m length is closed at one end. The air column in the pipe resonates at its fundamental frequency of 400 Hz. The number of nodes in the sound wave formed in the pipe is _____.

[Speed of sound = 320 m/s]

Ans. (5)

Sol. From question

Length of pipe is 1m

v = f = 400 H₂

v = 320 m/s

n = ??

We know that

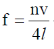
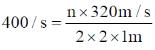
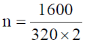
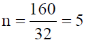
58. The critical angle of a crystal is 30°. Its Brewster angle is ______ degrees (Round off to the nearest integer).

Ans. (63)

Sol.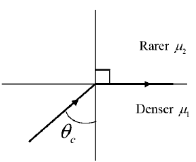

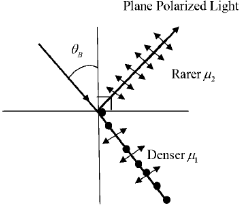
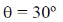
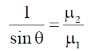
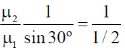
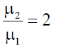
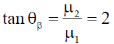
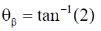
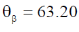
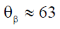
59.

Ans. (297 to 299)

Sol.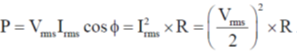

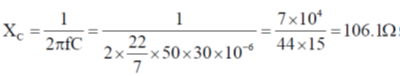
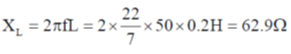
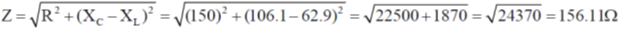
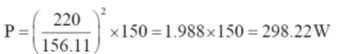
60. A charge q is uniformly distributed over the volume of a dielectric sphere of radius a. If the dielectric constant 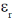= 2, then the ratio of the electrostatic energy stored inside the sphere to that stored outside is_______ (Round off to 1 decimal place).

Ans. (0.1)

Sol.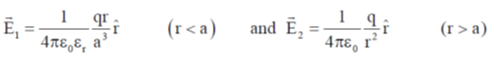

For r < a; Electrostatic energy