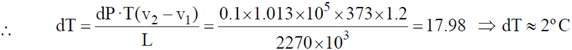1.    For an infinitely long wire with uniform line-charge density, 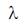, along the z-axis, the electric field at a point (a, b, 0) away from the origin is

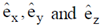    ( are unit vector in Cartesian - coordinate system)

    (a)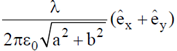

    (b)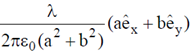

    (c)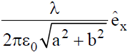

    (d)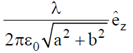

Ans.    (b)

Sol.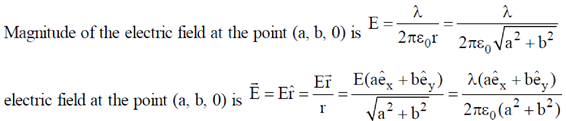    

2.    A 1W point source at origin emits light unifirmly in all the directions. If the units for both the axes are measured in centimetre, then the Poynting vector at the point (1, 1, 0) in W/cm² is

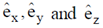( are unit vector in Cartesian - coordinate system)

 

    (a)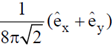

    (b)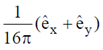

    (c)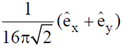

    (d)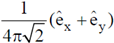

Ans.    (a)

Sol.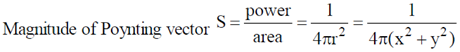    

    Magnitude of Poynting vector at the point (1, 1, 0) is

    

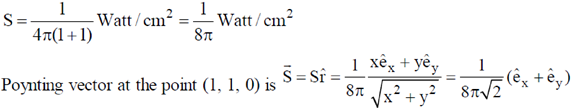
3.    A charged particle in a uniform magnetic field 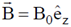starts moving from the origin with velocity 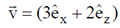m/s. The trajectory of the particle and the time t at which it reaches 2 meters above the xy-plane are

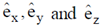( are unit vector in Cartesian - coordinate system)

 

    (a) Helical path; t = 1s

    (b) Helical path; t = 2/3 s

    (c) Circular path; t = 1s

    (d) Circular path; t = 2/3 s

Ans.    (a)

Sol.    From the given information in the question, we have 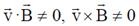i.e. velocity is neither paraller non perpendicular to the magnetic field. Therefore particle will move in helical path and the z-coordinate of the particle will be z = v_zt2 = 2 × t 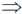t = 1 sec.

4.    Consider a particle of mass m following a trajectory given by x = x₀ cos 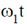and y = y₀ sin 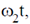where x₀, y₀, 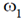and 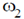are constants of appropriate dimensions. The force on the particle is

    (a)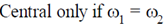

    (b)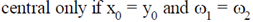

    (c) always central

    (d)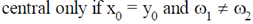

Ans.    (a)

Sol.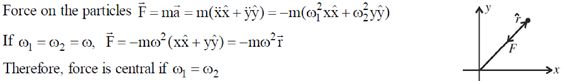    

5.    Which one of the following points represent the complex number =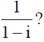

    (a)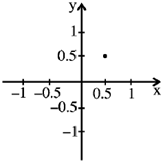

    (b)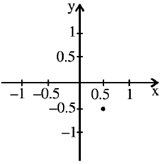

    (c)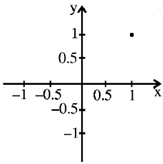

    (d)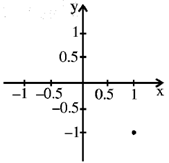

Ans.    (a)

Sol.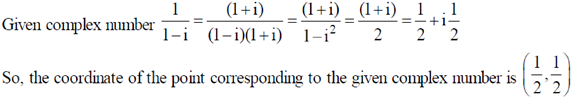    

6.    The eigenvalues of the matrix representing the following pair of linear equations

        x + iy = 0

        ix + y = 0    are

    (a) 1 + i, 1 + i

    (b) 1 – i, 1 – i

    (c) 1, i

    (d) 1 + i, 1 – i

Ans.    (d)

Sol.    Given pair of linear equations: x + iy = 0 and ix + y = 0

 

 

 

    

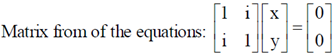
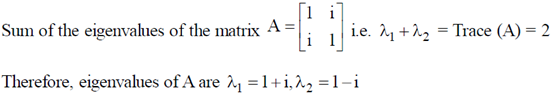
7.    The solution of the Boolean equation 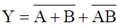is

    (a) 1

    (b)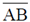

    (c)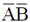

    (d)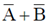

Ans.    (d)

Sol.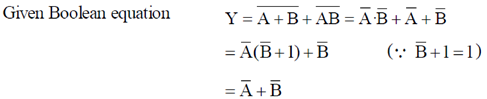    

8.    A spherical closed container with smooth inner wall contains a monoatomic ideal gas. If the collisions between the wall and the atoms are elastic, then the Maxwell speed-distribution function 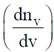for the atoms is best represented by

    (a)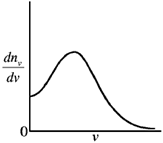

    (b)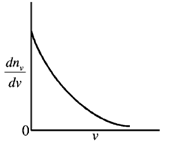

    (c)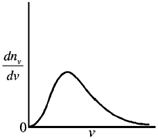

    (d)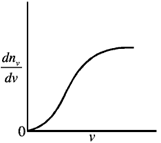

Ans.    (b)

Sol.    Maxwell speed distribution function is given by

    Phase difference is zero and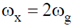

    

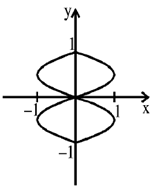
    The equation of sinnusoidal signals is given by

        x = 1 · sin 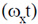and y = 1 · sin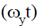

    Such that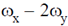     

9.    Two sinusoidal signals of frequencies 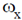and 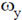having same amplitude are applied to x- and y-channels of a cathode ray oscilloscope (CRO), respectively. The following stationary figure will be observed when

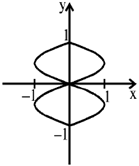
    (a)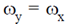

    (b) phase difference is 0

    (c)

    (d)

Ans.    (b)

Sol.    Correct option is (b)

10.    The phase difference 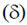between input and output voltage for the following circuits (i) and (ii)

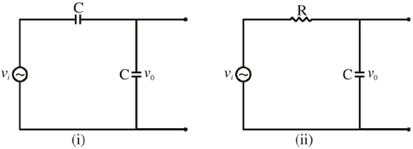
    will be

    (a) 0 and 0

    (b)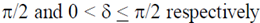

    (c)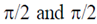

    (d)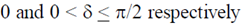

Ans.    (d)

Sol.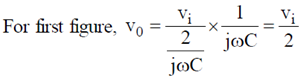    

    Therefore, the phase difference between input and output voltage is 0

    

11.    For the given set of equations:

        x + y = 1

        y + z = 1

        x + z = 1

    which one of the following statements is correct?

    (a) Equations are inconsistent

    (b) Equations are consistent and a single non-trivial solution exists

    (c) Equations are consistent and many solutions exist

    (d) Equations are consistent and only a trivial solution exists

Ans.    (b)

Sol.    Given set of equations: x + y = 1, y + z = 1, x + z = 1

    Matrix form of the equations: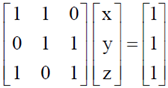

    The rank of the coefficient matrix 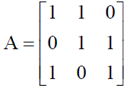and augamented matrix 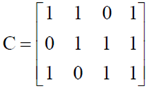are same and equal to the number of unknown variables i.e. 3.

    Therefore, equations are consistent and a single non-trivial solution exists.

    The solution will be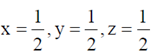    

12.    The tangent line to the curve x² + xy + 5 = 0 at (1, 1) is represented by

    (a) y = 3x – 2

    (b) y = –3x + 4

    (c) x = 3y – 2

    (d) x = –3y + 4

Ans.    (b)

Sol.    Given equation of curve: x² + xy + 5 = 0

    The unit normal vector to the curve at the point (1, 1) is 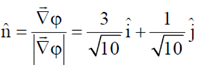and makes an angle 18.43º with positive x-axis. The line y = –3x + 4 will make an angle tan^–1(–3) = –71.57º with positive x axis i.e. it will be perpendicular to the unit normal vector and represents a tangent line to the given curve.

    Correct answer is (b)    

13.    In the following RC circuit, the capacitor was charged in two different ways.

    (i)    The capacitor was first charged to 5V by moving the toggle switch to position P and then it was charged to 10V by moving the toggle switch to position Q

   (ii)    The capacitor was directly charged to 10V, by keeping the toggle switch at position Q.

    Assuming the capacitor to be ideal, which one of the following statements is correct?

    

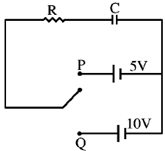
    (a) The energy dissipation in cases (i) and (ii) will be equal and non-zero

    (b) The energy dissipation for case (i) will be more than that for case (ii)

    (c) The energy dissipation for case (i) will be less than that for case (ii)

    (d) The energy will not be dissipated in either case

Ans.    (c)

Sol.    Case - I: Heat dissipated

    

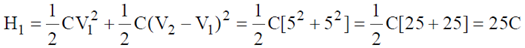
    Case - II: Heat dissipated

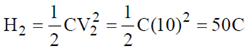
    Therefore, H₂ > H₁

14.    If a constant voltage + V is applied to the input of the following Op-Amp circuit for a time t, then the output voltage V₀ will approach

    

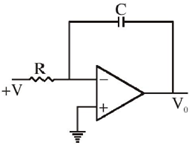
    (a) +V exponentially

    (b) –V exponentially

    (c) +V linearly

    (d) –V linearly

Ans.    (b)

Sol.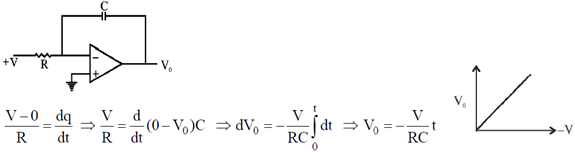    

15.    

    

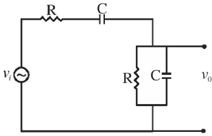
    (a)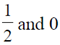

    (b)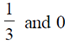

    (c)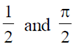

    (d)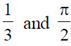

Ans.    (b)

Sol.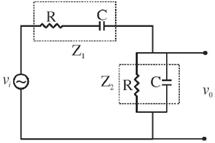    

    

    

    

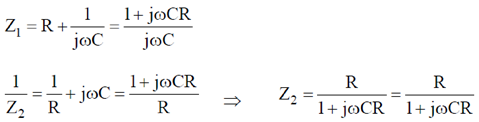
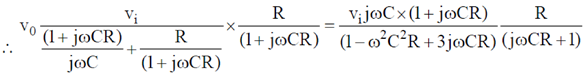
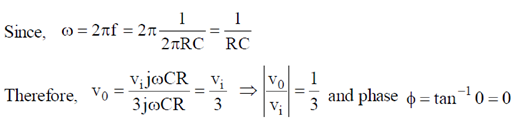
16.    Light travelling between two points takes a path for which

    (a) time of flight is always minimum

    (b) distance is always minimum

    (c) time of flight is extremum

    (d) distance is extremum

Ans.    (c)

Sol.    Fermat's principal: The path actually described by a ray of light in moving from one point to the other by way of a number of reflections or refractions is such that it always corresponds to the one for which the time taken is an extremum compared to the other nearby paths, that is, it is either a maximum or a minimum or stationary with respect to variations of that path.

17.    Consider a free electron (e) and a photon (ph) both having 10 eV of energy. If 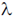and P represent wavelength and momentum respectively, then

    (mass of electron = 9.1 × 10^–31 kg; speed of light = 3 × 10⁸ m/s)

    (a)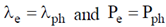

    (b)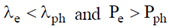

    (c)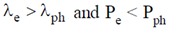

    (d)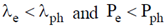

Ans.    (b)

Sol.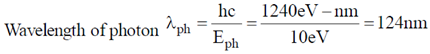    

    Wavelength of free electron

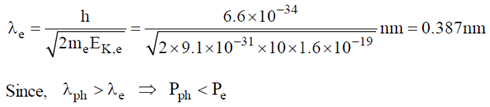
18.    For an ideal gas, which one of the following T-S diagram is valid?

    (a)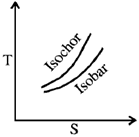

    (b)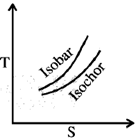

    (c)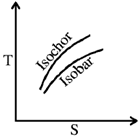

    (d)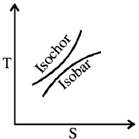

Ans.    (a)

Sol.    In T-S diagram, slope of isochoric curve = 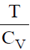and slope of isobaric curve =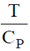

    As C_P > C_V, therefore, slope of isochoric curve > slope of isobaric curve.

    Since, slope of both curves is directly proportional with temperature T, therefore, slope of both curves will increase with an increament in T.    

19.    If U, F, H and G represent internal energy, Helmholtz free energy, enthalpy and Gibbs free energy respectively, then which one of the following is a correct thermodynamic relation?

    (a) dU = PdV – TdS

    (b) dH = VdP + TdS

    (c) dF = –PdV + SdT

    (d) dG = VdP + SdT

Ans.    (b)

Sol.    We know that,

    dU = TdS PdV, dH = TdS + VdP, dF = –SdT – PdV, dG = –SdT + VdP    

20.    A train passes through a station with a constant speed. A stationary observer at the station platform measures the tone of the train whistle as 484 Hz when it approaches the station and 442 Hz when it leaves the station. If the sound velocity in air in 330 m/s, then the tone of the whistle and the speed of the train are

    (a) 462 Hz, 54 km/h

    (b) 463 Hz, 52 km/h

    (c) 463 Hz, 56 km/h

    (d) 464 Hz, 52 km/h

Ans.    (a)

Sol.    When train approaches the station, the apparent frequency of the tone of the whistle

    

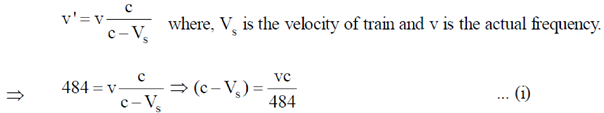
    When train leave the station, the apparent frequency of the tone of the whistle

    

    

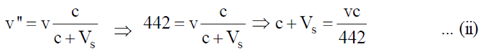
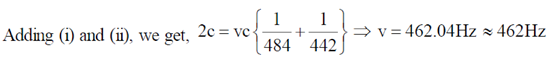
    Putting v = 462.04 Hz in equation (i), we get

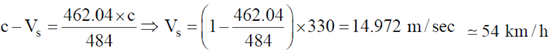
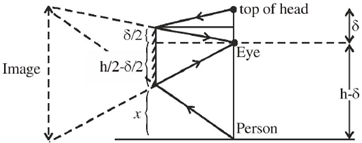
21.    The minimum length of a plane mirror to see the entire full length image of an object is half of the object's height. Suppose 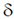is the distance between eye and top of the head of a person of height h. The person will be able to see his entire full-length image with a mirror of height h/2 fixed on the wall

    (a) When the bottom edge of mirror is kept h/2 above the floor

    (b)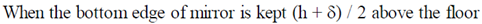

    (c)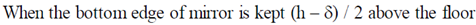

    (d) When the centre of the mirror is at the same height as centre of the person

Ans.    (c)

Sol.    Let mirror is at a height x above ground as shown in the figure

    

    

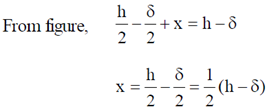
22.    A particle is moving in a plane with a constant radial velocity of 12 m/s and constant angular velocity of 2 rad/s. When the particle is at a distance r = 8m from the origin, the magnitude of

    (a)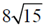

    (b) 20

    (c)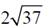

    (d) 10

Ans.    (b)

Sol.    Instantaneous velocity of the particle is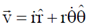

    Magnitude of the instantaneous velocity of the particle is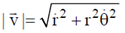

    

23.    A cylindrical rod of length L has a mass density distribution given by 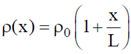, where x is measured from one end of the rod and 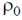is a constant of appropriate dimensions. The center of mass of the rod is

    (a)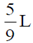

    (b)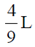

    (c)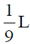

    (d)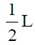

Ans.    (a)

Sol.    Centre of the mass of the rod

    

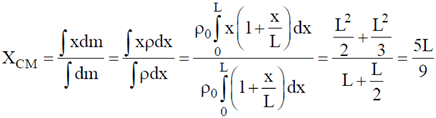
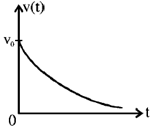
24.    A particle travels in a medium along a horizontal linear path. The initial velocity of the particle is v₀ and the viscous force acting on it is proportional to its instantaneous velocity. In the absence of any other forces, which one of the following figures correctly represents the velocity of the particle as a function of time?

    (a)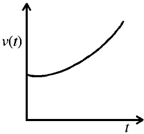

    (b)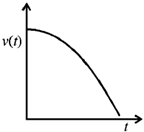

    (c)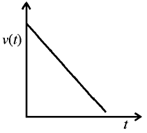

    (d)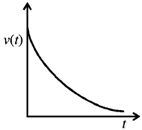

Ans.    (d)

Sol.    Equation of motion

    

    

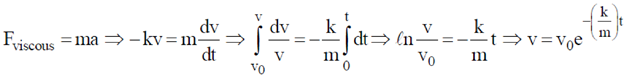
25.    A lightly damped harmonic oscillator with natural frequency 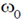is driven by a periodic force of frequency 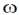. The amplitude of oscillation is maximum when

    (a)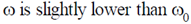

    (b)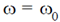

    (c)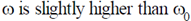

    (d) the force is in phase with the displacement

Ans.    (a)

Sol.    Correct answer is (a)

26.    A block of mass 0.38kg is kept at rest on a frictionless surface and attached to a wall with a spring of negligible mass. A bullet weighing 0.02 kg moving with a speed of 200 m/s hits the block at time t = 0 and gets stuck to it. The displacement of the block (in metre) with respect to the equilibrium position is given by

    

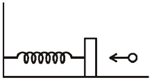
    (Spring constant = 640 N/m)

    (a) 2 sin 5t

    (b) cos 10t

    (c) 0.4 cos 25t

    (d) 0.25 sin 40t

Ans.    (d)

Sol.    Speed of block and bullet just after collision (using conservation of linear momentum)

    

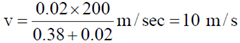
    If A be amplitude of oscillation then (using conservation of energy after collision) we get

    

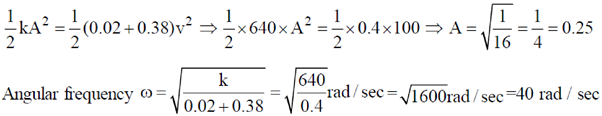
    Therefore, displacement of the block w.r.t. equilibrium position is x = A sin 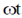= 0.25 sin 40 t

27.    One mole of an ideal gas with average molecular speed v₀ is kept in a container of fixed volume. If the temperature of the gas is increased such that the average speed gets doubled, then

    (a) the mean free path of the gas molecule will increase

    (b) the mean free path of the gas molecule will not change

    (c) the mean free path of the gas molecule will decrease

    (d) the collision frequency of the gas molecule with wall of the container remains unchanged

Ans.    (b)

Sol.    Mean free path of the gas molecule is given by

    

    

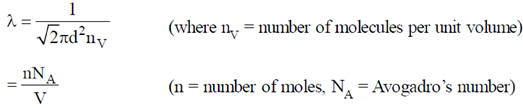
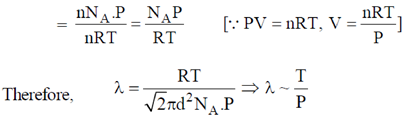
    As the temperature of the gas T is doubled, the pressure P will be doubled as 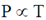at constant volume. Therefore, mean free path of the gas molecule 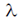will not changed.

28.    An arbitrarily shaped conductor encloses a charge q and is surrounded by a conducting hollow sphere as shown in the figure. Four different regions of space, 1, 2, 3 and 4 are indicated in the figure. Which one of the following statements is correct?

    

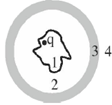
    (a) The electric field lines in region 2 are not affected by the position of the charge q

    (b) The surface charge density on the inner wall of the hollow sphere is uniform

    (c) The surface charge density on the outer surface of the sphere is always uniform irrespective of the position of charge q in region 1

    (d) The electric field in region 2 has a radial symmetry

Ans.    (c)

Sol.    Correct answer is (c)

29.    Consider a small bar magnet undergoing simple harmonic motion (SHM) along the x-axis. A coil whose plane is perpendicular to the x-axis is placed such that the magnet passes in and out of it during its motion. Which one of the following statements is correct? Neglect damping effects.

    (a) Induced e.m.f. is minimum when the center of the bar magnet crosses the coil

    (b) The frequency of the induced current in the coil is half of the frequency of the SHM

    (c) Induced e.m.f. in the coil will not change with the velocity of the magnet

    (d) The sign of the e.m.f. depends on the pole (N or S) face of the magnet which enters into the coil

Ans.    (a)

Sol.    Induced e.m.f. is minimum when the center of the bar magnet crosses the coil.

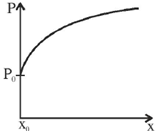
30.    An incompressible, non-viscous fluid is injected into a conical pipe at its orifice as schematically shown in the figure. The pressure at the orifice of area A₀ is P₀. Neglecting the effect of gravity and assuming steamline flow, which one of the following plots correctly predicts the pressure along axis of the cone?

    

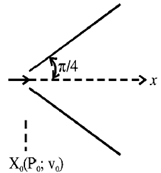
    (a)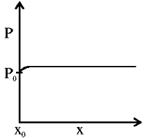

    (b)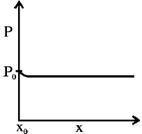

    (c)

    (d)

Ans.    (a)

Sol.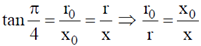    

    

    

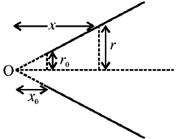
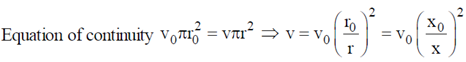
    According to Bernoulli's theorem,

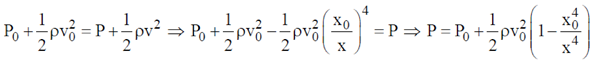
31.    Consider a spherical dielectric material of radius 'a', centered at origin. If the polarization vector , where P₀ is a constant of appropriate dimensions, then

    ( are unit vectors in Cartesian - coordinate system)

    (a) the bound volume charge density is zero

    (b) the bound surface charge density is zero at (0, 0, a)

    (c) the electric field is zero inside the dielectric

    (d) the sign of the surface charge density changes over the surface.

Ans.    (a, b, d)

Sol.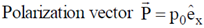    

    

    Bound volume charge density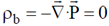

    Bound surface charge density

 

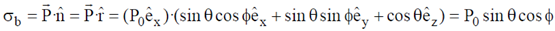
    Since 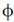varies from 0 to 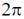over the surface of the sphere, therefore, the bound surface charge density changes its sign over the surface.

    Bound surface charge density at (0, 0, a) is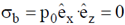    

32.    For an electric dipole with moment 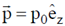placed at the origin, (p₀ is a constant of appropriate dimensions and 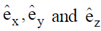are unit vectors in Cartesisn coordinate system)

    (a) potential falls as 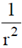, where r is the distance from origin

    (b) a spherical surface centered at origin is an equipotential surface

    (c) electric flux through a spherical surface enclosing the origin is zero

    (d) radial component of 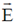is zero on the xy-plane

Ans.    (a, c, d)

Sol.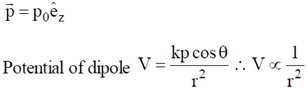    

    

    

    Electric flux through spherical surface enclosing the origin will be

    

33.    Three infinitely-long conductors carrying currents I₁, I₂ and I₃ lie perpendicular to the plane of the paper as shown below. If the value of integral 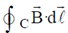for the loops C₁, C₂ and C₃ are 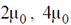, and 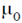in the units of N/A, respectively, then

    

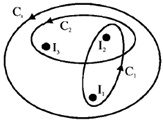
    (a) I₁ = 3A into the paper

    (b) I₂ = 5A out of the paper

    (c) I₃ = 0

    (d) I₃ = 1A out of the paper

Ans.    (a, b)

Sol.    From the diagram given in the question,

    

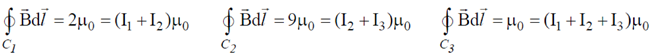
    Therefore, I₁ + I₂ = 2 ... (i)    I₂ + I₃ = 4 ... (ii)    I₁ + I₂ + I₃ = 1 ...(iii)

    using (i) and (ii) we get I₃ = –1A (into the paper)

    using (ii) and (iii) we get I₁ = –3A (into the paper)

    using (i) or (ii) we get I₂ = 5A (out of the paper)    

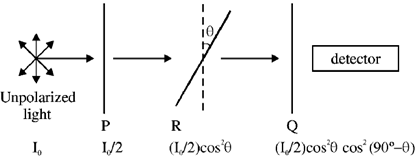
34.    In the optical arrangement as shown below, the axes of two polarizing sheets P and Q are oriented such that no light is detected. Now when a third polarizing sheet (R) is placed in between P and Q, then light is detected. Which of the following statement(s) is (are) true?

    

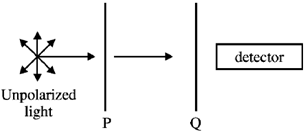
    (a) polarization axes of P and Q are perpendicular to each other

    (b) polarization axis of R is not parallel to P

    (c) polarization axis of R is not parallel to Q

    (d) polarization axes of P and Q are parallel to each other

Ans.    (a, b, c)

Sol.    The axes of two polarizing sheets P and Q should be perpendicular (crossed) to each other such that no light is detector.

    

    

    

35.    The P-V diagram below shows three possible paths for an ideal gas to reach the final state f from an initial state i. Which among the following statement(s) is(are) correct?

    

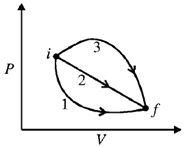
    (a) the work done by the gas is maximum along path-3

    (b) minimum change in the internal energy occurs along path-2

    (c) maximum heat transfer is for path-1

    (d) heat transfer is path independent

Ans.    (a)

Sol.    Work done is maximum along path 3

    Change in internal energy is same

    Maximum heat transfer is for path 3

    Heat transfer is path dependent    

36.    Potential energy U as a function of r is shown below. If a particle of mass m₁ and energy E₁, starting from r >> a, moves towards the origin, then

    

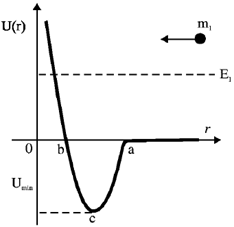
    (a) there is only one turning point for the particle

    (b) velocity of the particle starts to increase at r = a and reaches its maximum at r = c.

    (c) velocities of the particle at r = a and r = b are equal

    (d) the particle gets bounded if it elasticity collides with a stationary particle of mass m₂ at r = c, imparting a momentum greater than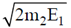

Ans.    (a, b, c, d)

Sol.    Using conservation of total mechanical energy, we can get information about speed.

    At turning points the total energy of the particle will be equal to potential energy i.e. kinetic energy of the particle is zero. Therefore, there is only one turning point of the particle.

    When potential is minimum speed is maximum and vice-versa.

    Energy imparted to m₂ is greater than 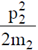i.e. greater than E₁ then energy of m₁ becomes negative.

    Therefore it will get bounded.    

37.    A particle moves in a circular path in xy-plane centered at the origin. If the speed of the particle is constant, then its angular momentum

    (a) about the origin is constant both in magnitude and direction

    (b) about (0, 0, 1) is constant in magnitude but not in direction

    (c) about (0, 0, 1) varies both in magnitude and direction

    (d) about (0, 0, 1) is constant in direction but not in magnitude.

Ans.    (a, b)

Sol.    Position vector of the particle w.r.t. origin (0,0,0) is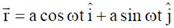

    Velocity of the particle w.r.t. origin (0,0,0) is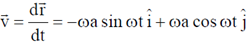     

    Angular momentum of the particle w.r.t. origin (0,0,0) is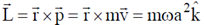

    Therefore, is constant both in magnitude and direction.

    Position vector of the particle w.r.t. origin (0,0,1) is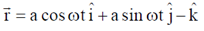

    Velocity of the particle w.r.t. origin (0, 0, 1) is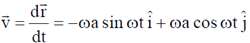

    Angular momentum of the particle w.r.t. origin (0, 0, 1) is

    

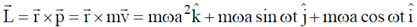
    Therefore, 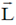is constant in magnitude but not in direction.    

38.    A pn junction was formed with a heavily doped (10¹⁸ cm^–3) p-region and lightly doped (10¹⁴ cm^–3) n-region. Which of the following statement(s) is(are) correct?

    (a) the width of the depletion layer will be more in n-side of the junction

    (b) the width of the depletion layer will be more in the p-side of the function

    (c) the width of the depletion layer will be same on both sides of the junction

    (d) if the pn junction is reverse biased, then the width of the depletion region increases.

Ans.    (a, d)

Sol.    For space change neutrality in the p-n junction

    

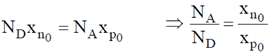
    Where    N_D = is the donor density, N_A = is the acceptor density    

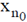         = is the width of the depletion region in n side

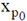         = is the width of the depletion region in p side.

    

    

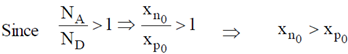
    If the p-n junction is reverse biased i.e. p side of the diode is connected with negative terminal of the battery and n side of the diode is connected with positive terminal of the battery. As a result holes and electrons will attracted towards outside. Therefore, width of the depletion region will increase.

39.    A slit has width d along the x-direction. If a beam of electrons, accelerated in y-direction to a particular velocity by applying a potential difference of 100 + 0.1 kV passes through the slit, then, which of the following statement(s) is(are) correct?

    (a) the uncertainty in the position of electrons in x-direction before passing the slit is zero

    (b) the momentum of electrons in x-direction is ~ 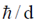immediately after passing the slit.

    (c) the uncertainty in the position of electrons in y-direction before passing the slit is zero

    (d) the presence of the slit does not affect the uncertainty in momentum of electrons in y-direction.

Ans.    (b, d)

Sol.    According to the given information in the question, we consider x-direction as the vertical direction and y-direction as the horizontal direction. Before the electrons passing the slit, we have more or less complete information about their momentum, but nothing on their position. We don't know where they are exactly, and we also don't know if they go through the slit or not. So they can be anywhere i.e. 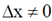and 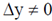. So, statements given in options (A) and (C) are incorrect.

    However, we do know their energy and momentum. The momentum will have only horizontal component (y-direction), as the electrons are accelerated in y-direction. Hence, their vertical momentum (x-direction) is zero, before they pass through the slit.

    After an electron goes through the slit and detected on the other side, then its vertical position (x) can be measured 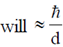with considerable accuracy. The uncertainty in vertical position (x) will be of the order of slit width d. From the diffraction pattern itself, we know that the electron acquires some vertical momentum (x-direction). Therefore, according to uncertainty principle, the vertical component (x-direction) of momentum of electrons will . So, statement given in option (B) is correct.

    After an electron goes through the slit and detected on the other side, its horizontal position (y) can be anywhere just like before. So, the uncertainty in the horizontal momentum (y-direction) of electrons will not be affected due to the presence of the slit. So, statement given in option (D) is correct.    

40.    A free particle of energy E collides with a one-dimensional square potential barrier of height V and width W. Which one of the following statement(s) is(are) correct?

    (a) for E > V, the transmission coefficient for the particle across the barrier will always be unity

    (b) for E < V, the transmission coefficient changes more rapidly width W than with V.

    (c) for E < V, if V is doubled, the transmission coefficient will also be doubled

    (d) sum of the reflection and transmission coefficient is always one

Ans.    (b, d)

Sol.    Variation of reflection coefficient R and transmission coefficient T w.r.t. energy E of the particle, incident on the potential barrier of height V and width W:

    

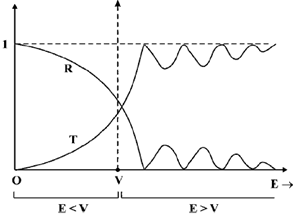
    For E > V, the transmission coefficient T is not always equal to unity. T varies sinusoidally with E an becomes unity for some specific values of E. So, statement given in option (A) is incorrect.

    For E < V, the transmission coefficient T is given by

        

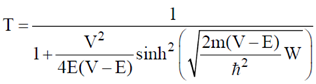
    From the expression it is clear that T will change more rapidly with W than with V. So statement given in option (B) is correct.

    If the height of the barrier V is doubled, then transmission coefficient T will decrease. So, statement given in option (C) is incorrect.

    It is clear from the plot that, sum of reflection and transmission coefficient is always one i.e. R + T = 1. So statement given in option (D) is correct.    

41.    Fourier series of a given function f(x) in the interval 0 to L is

    

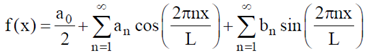
    If f(x) = x in the region (0, 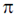), b₂ = _________________

Ans.    (–0.5)

Sol.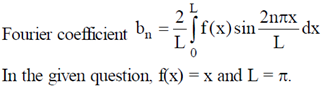    

    

42.    Consider a function f(x, y) = x³ + y³, where y represents a parabolic curve x² + 1. The total derivative of f with respect to x, at x = 1 is _________

Ans.    (27)

Sol.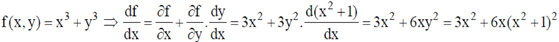    

    

43.    A rectangular area (A₁) is formed by two vectors and as shown in figure (i). A new set of vectors, representing the area (A₂) as shown in figure (ii), are given as: 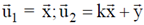where k is a dimensionless constant.

    

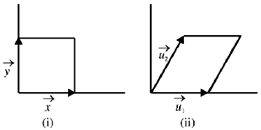
    The Jacobian of the frame 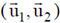with respect to 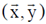is _________

Ans.    (1)

Sol.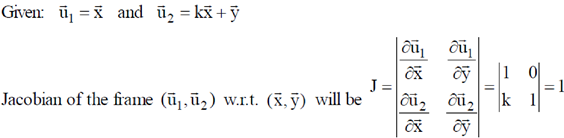    

44.    A particular radioisotope has a half-life of 5 days. In 15 days the probability of decay in percentage will be __________

Ans.    (87.5)

Sol.    Half-life of a particle radioisotope t_1/2 = 5 days. So, 15 days are equivaent to 3 half-lives.

    After 3 half-lives, the number of atoms present in the radioisotope sample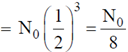

    (where N₀ is number of atoms in the radioisotope sample at t = 0)

    So, probability of decay =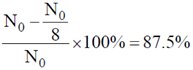     

45.    In a photoelectric experiment both sodium (work function = 2.3 eV) and tungsten (work function = 4.5 eV) metals were illuminated by an ultraviolet light of same wavelength. If the stopping potential for tungsten is measured to be 1.8 V, the value of the stopping potential for sodium will be _______V.

Ans.    (4)

Sol.    According to photoelectric equation, eV_s = hν – W₀, where V_s is the stopping potential, hν is the energy of the incident photon, W₀ is work function of the metal.

    For Tungsten, V_S = 1.8 V and W₀ = 4.5 eV. So, energy of the incident photon hν = 6.3 eV

    For Sodium, W₀ = 2.3 eV. So, stopping potential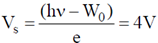     

    Correct answer is (4).    

46.    The addition of two binary numbers 1000.01 and 0001.11 in binary representation is __________

Ans.    (1010)

Sol.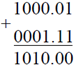    

47.    The number of second-nearest neighbor ions to a Na⁺ ion in NaCl crystal is _________

Ans.    (12)

Sol.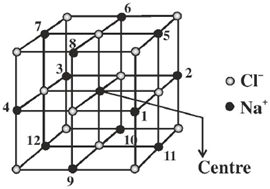    

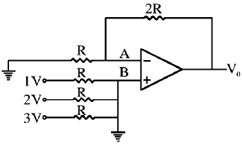
48.    The output voltage V₀ of the OPAMP circuit given below is _______________V.

    

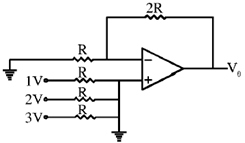
Ans.    (0)

Sol.    Since both A and B point have equal and zero input voltage so for ideal Op-Amp output voltage will be zero.

    

49.    A cylinder contains 16g of O₂. The work done when the gas is compressed to 75% of the original volume at constant temperature of 27ºC is _______________J.

    [Universal gas constant R = 8.31 J/(mole K)]    

Ans.    (–358.6)

Sol.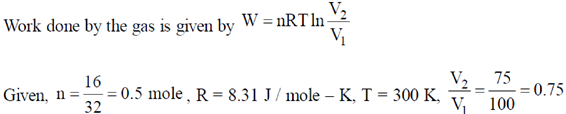    

    

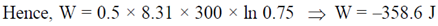
50.    When sunlight is focused on a paper using a bi-convex lens, it starts to burn in the shortest time if the lens is kept 0.5 m above it. If the radius of curvature of the lens is 0.75m then, the refractive index of the material is ____________.

Ans.    (1.75)

Sol.    For, a bi-convex lens,

    

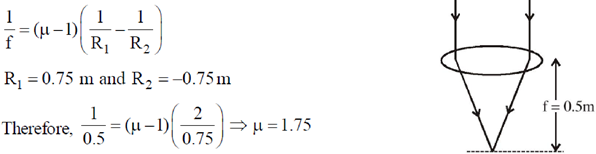
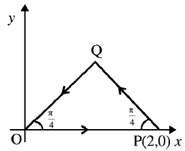
51.    Consider a closed triangular contour traversed in couter-clockwise direction, as shown in the figure below.

    

    

Ans.    (–2)

Sol.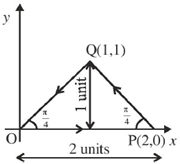    

    According to Stoke's theorem

    

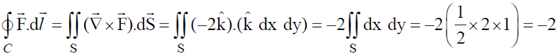
52.    A hemispherical shell is placed on the xy-plane centered at the origin. For a vector field 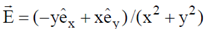, the value of the integral 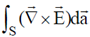over the hemispherical surface is ___________ π.

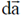    ( is the elemental surface area, 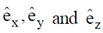are unit vectors in Cartesian - coordinate system)    

Ans.    (0)

Sol.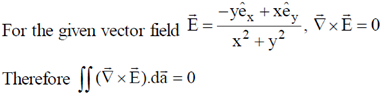    

53.    The shape of a dielectric lamina is defined by the two curves y = 0 and y = 1 – x². If the charge density of the lamina 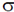= 15 y C/m², then the total charge on the lamina is _____________C.

Ans.    (8)

Sol.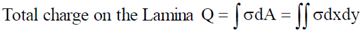    

    

    

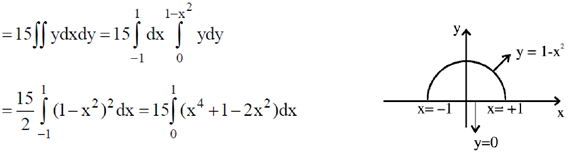
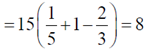
    Therefore, total charge on lamina is 8C.

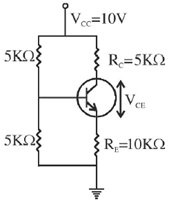
54.    In the circuit given below, the collector to emitter voltage V_CE is ______________V. (Neglect V_BE, take 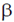= 100)

    

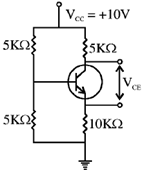
Ans.    (2.52)

Sol.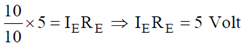    

    I_E = 0.5 × 10^–3 A = 0.5 mA

    

    

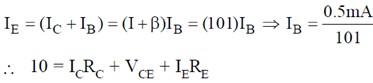
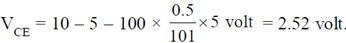
55.    The de-Broglie wavelength of a relativistic electron having 1 MeV of energy is __________×10^–12m. (Take the rest mass energy of the electron to be 0.5 MeV. Planck constant = 6.63 × 10^–34 Js, speed of light = 3 × 10⁸ m/s, electronic charge = 1.6 × 10^–19 C)

Ans.    (1.43)

Sol.    For a relativistic electron

    

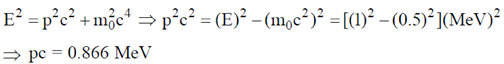
    De-Broglie wavelength of the electron

    

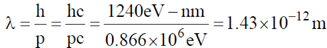
56.    X-ray diffraction of cubic crystal gives an intensity maximum for Bragg angle of 20º corresponding to the (110) plane. The lattice parameter of the crystal is __________nm.

    (Consider wavelength of X-ray = 0.15 nm)    

Ans.    (0.31)

Sol.    According to Bragg's law,    2d sin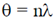     

    where, d is the interplanar spacing, 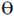is the angle of diffraction, n is the order of diffraction and 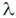is the wavelength of the light.

    

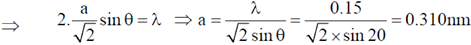
57.    X-rays of 20 KeV energy is scattered inelastically from a carbon target. The kinetic energy transferred to the recoiling electron by photons scattered at 90º with respect of the incident beam is ___________KeV.

    (Planck constant = 6.6 × 10^–34 Js, speed of light = 3 × 10⁸ m/s, electron mass = 9.1 × 10^–31 kg, electronic charge = 1.6 × 10^–19 C).    

Ans.    (0.75)

Sol.    In Compton effect experiment, the kinetic energy transferred to the recoil electron by photons is

    

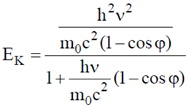
    where 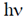= energy of the X-ray photon = 20 KeV, m₀c² = rest mass energy of the electron = 511 KeV, 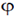= angle of scattering = 90º.

    Therefore, E_K = 0.75 KeV    

58.    An aluminum plate of mass 0.1 kg at 95ºC is immersed in 0.5 litre of water at 20ºC kept inside an insulating container and is then removed. If the temperature of the water is found to be 23ºC, then the temperature of the aluminum plate is _____________ºC. (The specific heat of water and aluminum are 4200 J/kg-K and 900 J/kg-K respectively, the density of water is 1000 kg/m³).

Ans.    (25)

Sol.    Heat given by aluminium plate = Heat taken by water

    

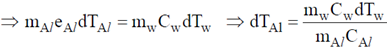
    Given,    m_w = 1000 × 0.5 × 10^–3 kg = 0.5 kg, C_w = 4200 J/kg-K    

    dT_w = 23ºC – 20ºC = 3ºC, m_Al = 0.1 kg, C_Al = 900 J / kg – K

    

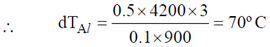
    Therefore, temperature of Al plates is 25ºC

    Correct answer is (25).

59.    The maximum and minimum speeds of a comet that orbits the Sun are 80 and 10 km/s respectively. The ratio of the aphelion distance of the comet of the radius of the Earth's orbit is _________. (Assume that Earth moves in a circular orbit of radius 1.5 × 10⁸ km with a speed of 30 km/s).

Ans.    (2)

Sol.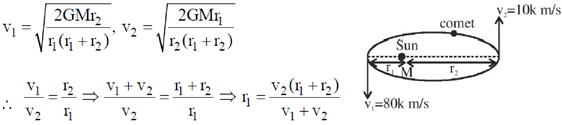    

    

    

    

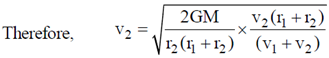
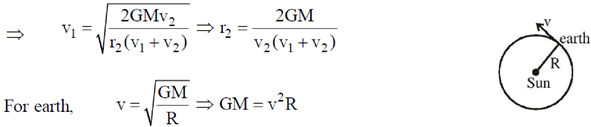
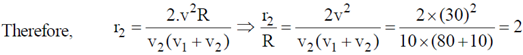
60.    If there is a 10% decrease in the atmospheric pressure at a hill compared to the pressure at sea level, then the change in the boiling point of water is _______________ºC.

    (Take latent heat of vapourisation of water as 2270 kJ/kg and the change in the specific volume at the boiling point to be 1.2 m³/kg).    

Ans.    (2)

Sol.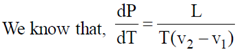    

    Given,    L = 2270 kJ / kg, (v₂ – v₁) = 1.2 m³ / kg, T = 373 K    

    dP = 10% of atm pressure = 0.1 × 1.013 × 10⁵ N/m²