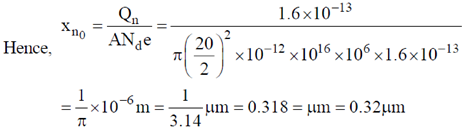1. A system consists of N number of particles, N >> 1. Each particle can have only one of the two energies E₁ or E₁ + 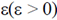. If the system is in equilibrium at a temperature T, the average number of particles with energy E₁ is

(a)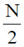

(b)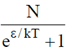

(c)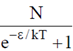

(d)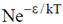

Ans. (c)

Sol.

Now N₁ + N₂ = N M – B distribution

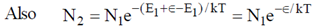
Now, N₁ + N₂ = N

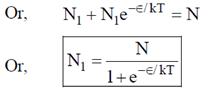
2. Temperature dependence of resistivity of a metal can be described by

(a)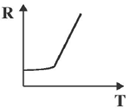

(b)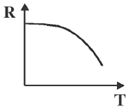

(c)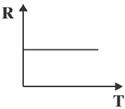

(d)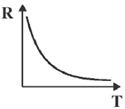

Ans. (a)

Sol. We know that total resistivity of a metal is given by

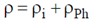
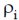is residual resistivity, is due to scattering by impurities. This is independent of temperature

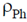is called the ideal resistivity, is due to scattering phonons. This is temperature dependent

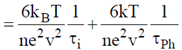
3. A charge q is at the centre of two concentric spheres. The outward electric flux through the inner sphere is 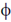while that through the outer sphere is 2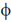. The amount of charge contained in the region between the two sphere is

(a) 2q

(b) q

(c) –q

(d) –2q

Ans. (b)

Sol. For sphere 1:

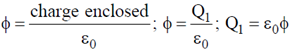
For sphere 2:

Therefore charge enclosed by outer sphere is twice charge enclosed by inner sphere.

Therefore charge contained in region between two sphere must be q.

4. At room temperature, the speed of sound in air is 340 m/sec. An organ pipe with both ends open has a length L = 29 cm. An extra hole is created at the position L/2. The lowest frequency of sound produced is

(a) 293 Hz

(b) 586 Hz

(c) 1172 Hz

(d) 2344 Hz

Ans. (c)

Sol. Effective length of organ pipe

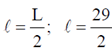
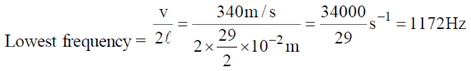
5. A proton from outer space is moving towards earth with velocity 0.99c as measured in earth's frame. A spaceship, traveling parallel to the proton, measures proton's velocity to be 0.97 c. The approximate velocity of the spaceship, in the earth's frame is

(a) 0.2c

(b) 0.3c

(c) 0.4c

(d) 0.5c

Ans. (c)

Sol.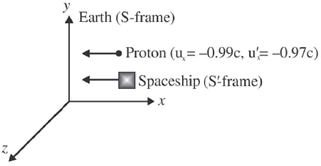

According to velocity-addition theorem

 

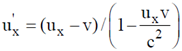
where, u_x = velocity of the proton w.r.t. earth i.e. S frame = –0.99 c

u'_x = velocity of the proton w.r.t. spaceship i.e. S´ frame = –0.97 c

v = velocity of the spaceship w.r.t. earth i.e. S frame

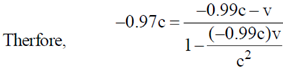
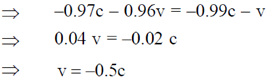
6. A particle with energy E is incident on a potential given by

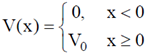
The wave function of the particle for E < V₀, in the region x > 0 (in terms of positive constants A, B and k) is

(a) Ae^kx + Be^–kx

(b) Ae^–kx

(c) Ae^ikx + Be^–ikx

(d) Zero

Ans. (b)

Sol.

Time independent Schrodinger equation for the region x > 0 is,

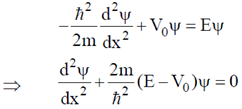
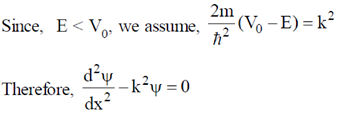
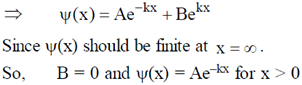
7. The electric field of a light wave is given by

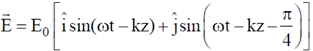
The polarization state of the wave is

(a) Left handed circular

(b) Right handed circular

(c) Left hand elliptical

(d) Right handed elliptical

Ans. (c)

Sol. We have,

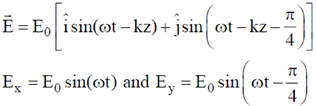
From the analysis of Lissajou figures

 

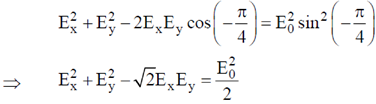
We know that this is the equation ellipse.

For the handedness.

 

 

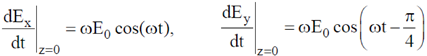
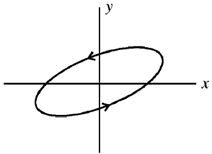
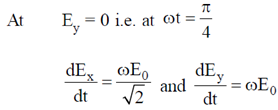
Both are positive. So the figure is like

This is the left handed ellipse.

8. A mass m, lying on a horizontal, frictionless surface, is connected to one end of a spring. The other end of the Spring is connected to a wall, as shown in the figure. At t = 0, the mass is given an impulse

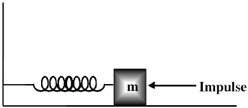
The time dependence of the displacement and the velocity of the mass (in terms of non-zero constants A and B) are given by

(a)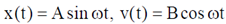

(b)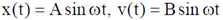

(c)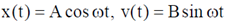

(d)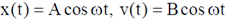

Ans. (a)

Sol.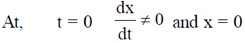

Option (a) satisfies this condition

9. Consider the coordinate transformation 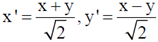. The relation between the area elements dx'dy' and dxdy is given by dx'dy' = jdxdy. The value of J is

(a) 2

(b) 1

(c) –1

(d) –2

Ans. (c)

Sol.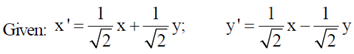

Relation between the area elements:

dx'dy' = Jdxdy

where J is jacobian of (x´, y´) w.r.t. (x, y) and given by

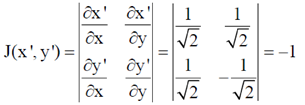
10. The trace of a 2 × 2 matrix is 4 and its determinant is 8. If one of the eigenvalue is 2(1 + i), the other eigenvalue is

(a) 2(1 – i)

(b) 2(1 + i)

(c) (1 + 2i)

(d) (1 – 2i)

Ans. (a)

Sol. Sum of the eigenvalues = Trace of the matrix

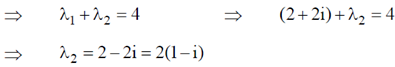
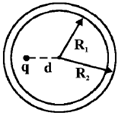
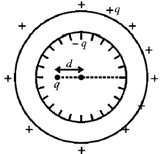
11. A hollow, conducting spherical shell of inner radius R₁ and outer radius R₂ encloses a charge q inside, which is located at a distance d(< R₁) from the centre of the spheres. The potential at the centre of the shell is

(a) zero

(b)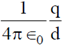

(c)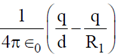

(d)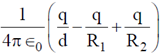

Ans. (d)

Sol. Due to induction –q and +q charges appear on the inner and outer surface of the shell.

So, potential at center will be

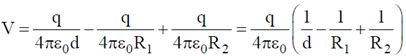
12. Doppler effect can be used to measure the speed of blood through vessels. Sound of frequency 1.0522 MHz is sent through the vessels along the direction of blood flow. The reflected sound generates a beat signal of frequency 100 Hz. The speed of sound in blood is 1545 m/sec. The speed of blood through the vessel, in m/sec, is

(a) 14.68

(b) 1.468

(c) 0.1468

(d) 0.01468

Ans. (c)

Sol. Let we denote the velocity of blood by v_B. Since the blood is flowing in the direction of propagation of wave. So, the frequency of reflected wave is

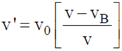
where, v₀ = 1.0522 MHz, v = 1545 m/s beat frequency = 100 Hz

= 100 × 10^–6 MHz = 0.0001 MHz = v₀ – v´.

So, v'v = v₀v – v₀v_B

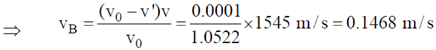
13. Vibrations of diatomic molecules can be represented as those harmonic oscillators. Two halogen molecules X₂ and Y₂ have fundamental vibrational frequencies v_x = 16.7 × 10¹² Hz and v_y = 26.8 × 10¹² Hz respectively. The respective force constants are K_x = 325 N/m and K_Y = 446 N/m. The atomic masses of F, Cl and Br are 19.0, 35.5 and 79.9 atomic mass unit respectively. The halogen molecules X₂ and Y₂ are

(a) X₂ = F₂ and Y₂ = Cl₂

(b) X₂ = Cl₂ and Y₂ = F₂

(c) X₂ = Br₂ and Y₂ = F₂

(d) X₂ = F₂ and Y₂ = Br₂

Ans. (b)

Sol. Vibrational frequencies can be written as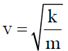

where k is the force constant and m is the reduced mass of the diatomic molecules.

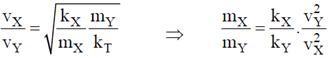
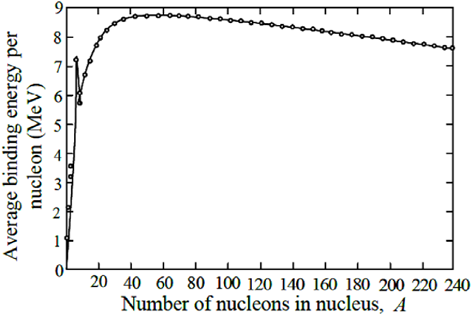
14. The variation of binding energy per nucleus with respect to the mass of nuclei is shown in the figure

Consider the following reactions:

which one of the following statements is true for the given decay modes of ?

(a) both 1 and 2 are allowed

(b) both 1 and 2 are forbidden

(c) 1 is forbidden and 2 is allowed

(d) 1 is allowed and 2 is forbidden

Ans. (c)

Sol. 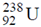is a radioactive element and will decay into various daughter nuclei by emitting and 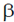particle.

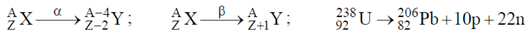
By the emission of p and n, atomic number decreases by 10 units and number is decreased by 32 units. i.e. there should be 8 number of 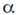-emission and 6 number of 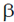-emission.

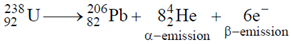
So, first reaction is forbidden and second reaction is allowed.

15. A rigid and thermally isolated tank is divided into two compartments of equal volume V, separated by a thin membrane. One compartment contains one mole of an ideal gas A and the other compartment contains one mole of a different ideal gas B. The two gases are in thermal equilibrium at a temperature T. If the membrane ruptures, the two gases mix. Assume that the gases are chemically inert. The change in the total entropy of the gases on mixing is

(a) 0

(b) R ln 2

(c)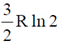

(d) 2R ln 2

Ans. (d)

Sol. The change in entropy due to diffusion / mixing of any number of inert gases is equal to h.

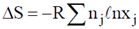
where, n_j is number of moles of j^m gas.

x_j is mole fraction of j^m gas.

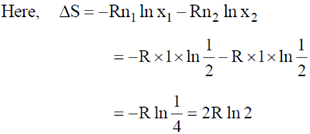
16. A zener regulator has an input voltage in the range 15V – 20 V and a load current in the range of 5 mA – 20 mA. If the zener voltage is 6.8 V, the value of the series resistor should be

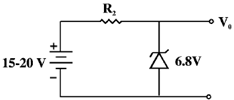
(a)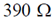

(b)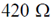

(c)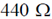

(d)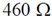

Ans. (b, c, d)

Sol.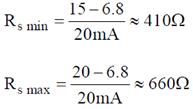

Any of the 3 options satisfied (b), (c), (d)

17. A positively charged particle, with a charge q, enters a region in which there is a uniform electric field and a uniform magnetic field 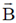, both directed parallel to the positive y-axis. At t = 0, the particle is at the origin and has a speed v₀ directed along the positive x-axis. The orbit of the particle, projected on the x-z plane, is a circle. Let T be the time taken to complete one revolution of this circle. The y-coordinate of the particle at t = T is given by

(a)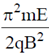

(b)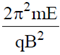

(c)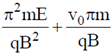

(d)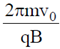

Ans. (b)

Sol. Displacement in y-direction will arise due to electric force.

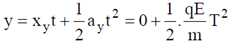
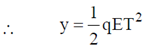
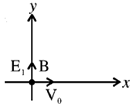
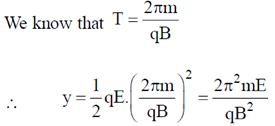
18. A satellite moves around the earth in a circular orbit of radius R centered at the earth. A second satellite moves in an elliptic orbit of major axis 8R, with the earth the one of the foci. If the former takes 1 day to complete a revolution, the letter would take

(a) 21.6 days

(b) 8 days

(c) 3 hours

(d) 1.1 hours

Ans. (b)

Sol. Using Keplers third law we get

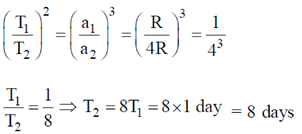
19. A system comprise of three electrons. There are three single particle energy levels accessible to each of these electrons. The number of possible configurations for this system is

(a) 1

(b) 3

(c) 6

(d) 7

Ans. (d)

Sol. Number of possible configuration

20. A rigid triangular molecule consists of three non-collinear atoms joined by rigid rods. The constant pressure molar specific heat (C_P) of an ideal gas consisting of such molecules is

(a) 6R

(b) 5R

(c) 4R

(d) 3R

Ans. (c)

Sol. For a rigid triangular molecule.

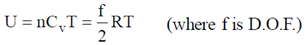
Here, f = 3 + 3 = 6

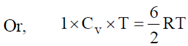
Or, C_V = 3R

Or, C_P = C_v + R = 4R

21. Consider the equation 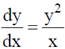with the boundary condition y(1) = 1. Out of the following, the range of x in which y is real and finite, is

(a)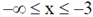

(b)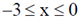

(c)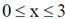

(d)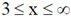

Ans. (d)

Sol.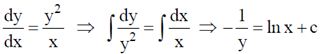

Applying the condition, y(1) = 1

We get, c = –1

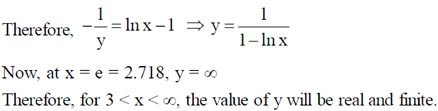
22. Consider a vector field 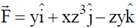. Let C be the circle x² + y² = 4 on the plane z = 2, oriented counter-clockwise. The value of contour integral 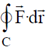is

(a)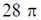

(b)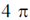

(c)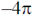

(d)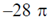

Ans. (a)

Sol.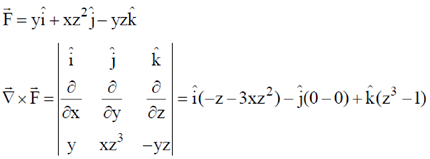

Now, using stoke's theorem

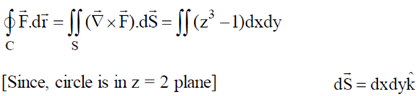
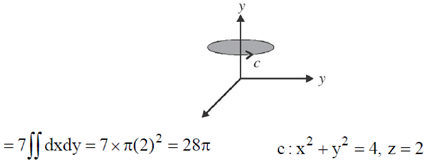
23. Which of the following circuits represent the Boolean expression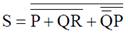

(a)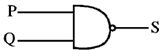

(b)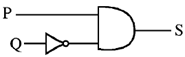

(c)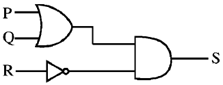

(d)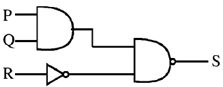

Ans. (b)

Sol.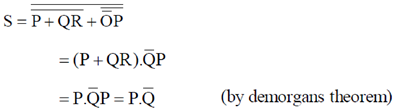

24. Seven uniform disks, each of mass m and radius r, are inscribed inside a regular hexagon, as shown. The moment of inertia of this system of seven disks, about an axis passing through the central disk and perpendicular to the plane of the disks, is

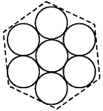
(a)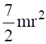

(b) 7 mr²

(c)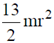

(d)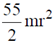

Ans. (d)

Sol. Moment of inertia of disc 2 about a perpendicular axis through center of disc 1 is

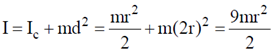
Therefore, total moment of inertia of system given is

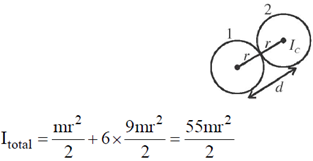
25. A nucleus has a size of 10^–15 m. Consider an electron bound within a nucleus. The estimated energy of this electron is of the order of

(a) 1 MeV

(b) 10² MeV

(c) 10⁴ MeV

(d) 10⁶ MeV

Ans. (b)

Sol. Nucleus size 10^–15 m

Maximum uncertainty in the position of the particle (e^–) within the nucleus = 10^–15 m

So, minimum uncertainty in the momentum of the particle (e^–)

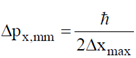
Energy of the electron within the nucleus.

26. A conducting wire is in the shape of a regular hexagon, which is inscribed inside an imaginary circle of radius R, as shown. A current I flows through the wire. The magnitude of the magnetic field at the centre of the circle is

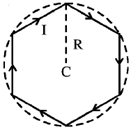
(a)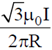

(b)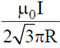

(c)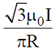

(d)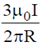

Ans. (c)

Sol. Magnetic field at C due to one side of hexagon is

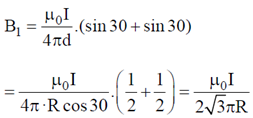
Total magnetic field at the center

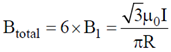
27. An observer is located on a horizontal, circular turntable which rotates about a verticle axis passing through its centre, with a uniform angular speed of 2 rad/sec. A mass of 10 grams is sliding without friction on the turntable. At an instant when the mass is at a distance of 8 cm from the axis, it is observed to move towards the centre with a speed of 6 cm/sec. The net force on the mass, as seen by the observer at that instant, is

(a) 0.0024N

(b) 0.0032 N

(c) 0.004 N

(d) 0.006 N

Ans. (c)

Sol. Net force on observer is resultant of centrifugal and coriolis forces

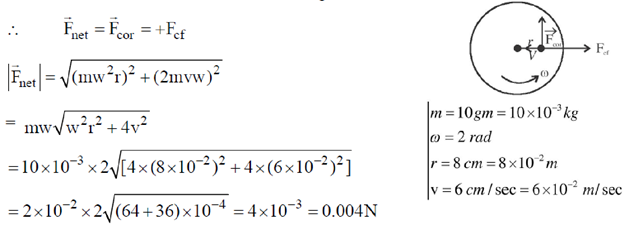
28. The Fourier series for an arbitrary periodic function with period 2L is given by 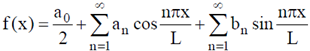. For the particular periodic function shown in the figure, the value of a₀ is

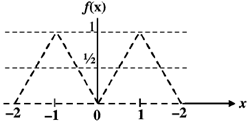
(a) 0

(b) 0.5

(c) 1

(d) 2

Ans. (c)

Sol. Functional form:

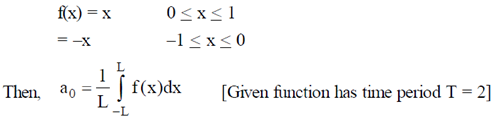
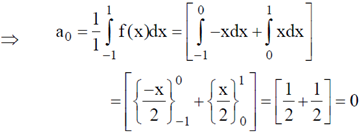
29. Miller indices of a plane in cubic structure that contains all the directions [100], [011] and [111] are

(a) (011)

(b) (101)

(c) (100)

(d) (110)

Ans.

Sol. All options are wrong.

30. The phase of the complex number (1 + i)i in the polar representation is

(a)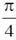

(b)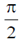

(c)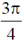

(d)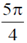

Ans. (c)

Sol. z = (1 + i) i = i – 1 = –1 + i

Phase of complex number

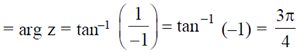
31. For an electromagnetic wave travelling in free space, the electric field is given by 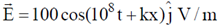. Which of the following statements are true?

(a) The wavelength of the wave in meter is 6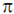

(b) The corresponding magnetic field is directed along the positive z-direction

(c) The poynting vector is directed along the positive z-direction

(d) The wave is linearly polarized.

Ans. (a, d)

Sol.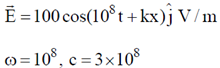

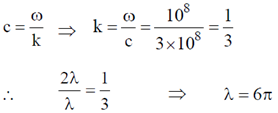
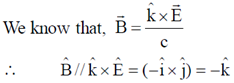
Magnetic field is in negative z-direction poynting vector is indirection of propagation (–x)

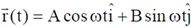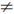32. A particle of mass m is moving in x-y plane. At any given time t, its position vector is given by , where A, B and are constants with A B. Which of the following statements are true?

(a) orbit of the particle is an ellipse

(b) speed of the particle is constant

(c) at any given time t, the particle experiences a force towards origin

(d) the angular momentum of the particle is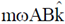

Ans. (a, c, d)

Sol.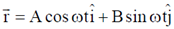

Its a superposition of two SHM's, of unequal amplitude and phase difference of . So, orbit is elliptical.

 

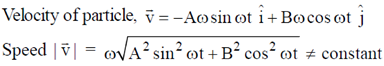
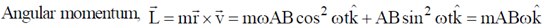
33. Muons are elementary particles produced in the upper atmosphere. They have a life time of 2.2 µs. Consider muons which are travelling vertically towards the earth's surface at a speed of 0.998c. For an observer on earth, the height of the atmosphere above the surface of the earth is 10.4 km. Which of the following statements are true?

(a) the muons can never reach earth's surface.

(b) the apparent thickness of earth's atmosphere in muon's frame of reference is 0.96 km.

(c) the lifetime of muons in earth's frame of reference is 34.8 µs

(d) muons travelling at a speed greater than 0.998c reach the earth's surface.

Ans. (c, d)

Sol. Proper life time of the muon 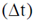(w.r.t. body frame of muon) = 2.2 µs

Speed of muon w.r.t. observer on earth, v = 0.998 c.

Lifetime of muon w.r.t. earth's frame

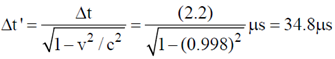
Proper thickness of earth's atmosphere in earth's frame L = 10.4 km.

Apparent thickness of earth's atmosphere in muon's frame.

 

 

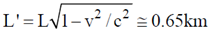
Time taken by the muon to reach the earth's surface in earth frame.

As the speed of the muon increases, life time of the muon increases and time taken by the muon to reach earth's surface decreases.

34. In an ideal op-amp circuit shown below, R₁ = 3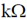 and R₂ = 1 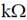and V_i = 0.5 sin 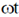(in volt). Which of the following statements are true?

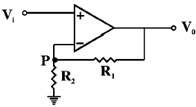
(a) the current through R₁ = the current through R₂.

(b) the potential at P is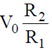

(c) the amplitude of V₀ is 2V.

(d) the output voltage V₀ is in phase with V_i.

Ans. (a, c, d)

Sol. The current through R₁ and R₂ are same

(A) (a) satisfied (B) (b) wrong (C) (c) satisfied (D) (d) satisfied

35. Consider the circuit consisting of an AC function generator V(t) = V₀ sin with V₀ = 5V, an inductor L = 8.0 mH, resistor R = 5W and a capacitor C = 100 µF. Which of the following statements are true if we vary the frequency?

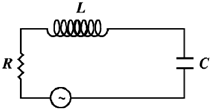
(a) the current in the circuit would be maximum at v = 178 Hz.

(b) the capacitor reactance increases with frequency

(c) at resonance, the impedance of the circuit is equal to the resistnace in the circuit

(d) at resonance, the current is out of phase with source voltage.

Ans. (a, c)

Sol. Resonance frequency,

(a) satisfied (b) failed (c) satisfied (d) wrong

36. The following figure shows a double slit Fraunhofer diffraction pattern produced by two slits, each of width a, separated by a distance b, a < b. Which of the following statements are correct?

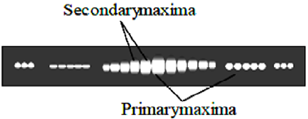
(a) reducing a increases the separation between consecutive primary maxima

(b) reducing a increases the separation between consecutive secondary maxima

(c) reducing b increases the separation between consecutive primary maxima

(d) reducing b increases the separation between consecutive secondary maxima

Ans. (a, d)

Sol. Here the primary maxima are the diffraction maxima.

We know that spacing between diffraction maxima increases by decreasing the slit width a. Within the diffraction maxima, secondary maxima occur due to interference and by decreasing b the spacing between secondary maxima increases. So, a has effect only on the primary maxima (diffraction maxima) while b has effect only on secondary maxima (interference maxima within the diffraction maxima). It should be noted that for primary maxima condition for diffraction as well as interference maxima must be satisfied.

37. A rod is hanging vertically from a pivot. A particle, travelling in horizontal direction, collides with the rod as shown in the figure. For the rod-particle system. Consider the linear momentum and the angular momentum about the pivot. Which of the following statements are not true?

(a) both linear momentum and angular momentum are conserved

(b) linear momentum is conserved but angular momentum is not

(c) linear momentum is not conserved but angular momentum is conserved.

(d) neither linear momentum nor angular momentum are conserved.

Ans. (b, c, d)

Sol. If we assume that it is about just before and just after collision then angular momentum about the pivot is conserved.

However if instants just before and just after collision is not considered and gravity is assumed to be present then neither linear momentum nor angular momentum is conserved.

38. As shown in the P-V diagram. AB and CD are two isotherms at temperatures T₁ and T₂ respectively (T₁ > T₂). AC and BD are two reversible adiabats. In this Carnot cycle, which of the following statements are true?

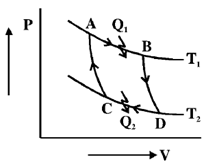
(a)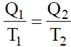

(b) the entropy of the source decreases

(c) the entropy of the system increases

(d) work done by the system W = Q₁ – Q₂

Ans. (a, d)

Sol. As the cycle is Carnot.

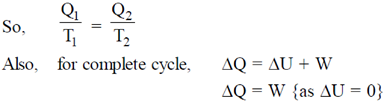
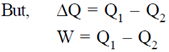
In a reversible carbon cycle, the entropy change of system as well as source is zero.

39. A unit cube made of dielectric material has a polarization 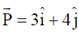units. The edges of the cube are parallel to the Cartesian axes. Which of the following statements are true?

(a) the cube carries a volume bound charge of magnitude 5 units.

(b) there is a charge of magnitude 3 units on both the surfaces parallel to the y-z plane

(c) there is a charge of magnitude 4 units on both the surfaces parallel to the x-z plane.

(d) there is a net non-zero induced charge on the cube

Ans. (b, c)

Sol.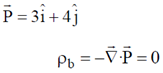

So volume bound charge in zero.

Now, surface bound charge,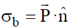

On surface parallel to y-z plane

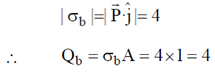
40. A particle is moving in a two-dimensional potential well

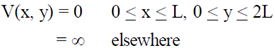
which of the following statements about the ground state energy E1 and ground state eigenfunction 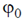are true?

(a)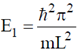

(b)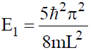

(c)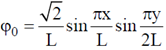

(d)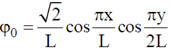

Ans. (b, c)

Sol. Given: Two dimensional potential well

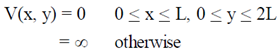
Wave function of the particle in such potential well

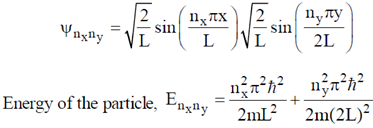
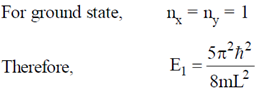
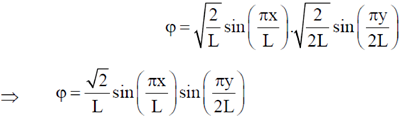
41. In an experiment on charging of an initially uncharged capacitor, an RC circuit is made with the resistance R = 10 and the capacitor C = 1000 µF along with a voltage source of 6V. The magnitude of the displacement current through the capacitor (in µA), 5 seconds after the charging has started is __________.

Ans. (363.92)

Sol. Current in the circuit after time t is,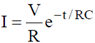

Displacement current between the plates is equal to the current in the wire.

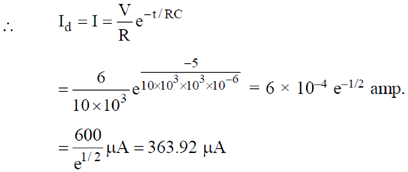
42. X-rays of wavelength 0.24 nm are Compton scattered and the scattered beam is observed at an angle of 60º relative to the incident beam. The Compton wavelength of the electron is 0.00243 nm. The kinetic energy of scattered electrons in eV is ___________

Ans. (26)

Sol.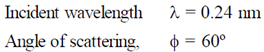

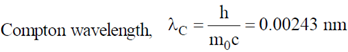
Kinetic energy of scattered electron E_k = loss in energy of X-ray photon

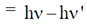
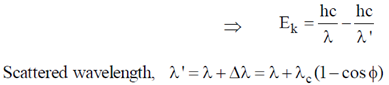
= (0.24 + 0.001215) nm = 0.241215 nm

43. GaAs has a diamond structure. The number of GaAs bonds per atom which have to be broken to fracture the crystal in the (001) plane is __________

Ans. (2)

Sol. Correct answer is (2)

44. A diode at room temperature (kT = 0.025 eV) with a current of 1 µA has a forward bias voltage V_f = 0.4 V.For V_f = 0.5 V, the value of the diode current (in µA) is __________

Ans. (54.598)

Sol. kT = 0.025 eV

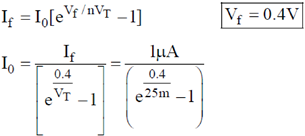
I₀ = 1.125 × 10^–13 A

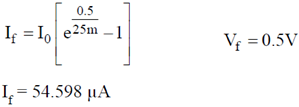
45. The power radiated by sun is 3.8 × 10²⁶ W and its radius is 7 × 10⁵ km. The magnitude of the poynting vector (in W/cm²) at the surface of the sun is __________

Ans. (6174.4)

Sol.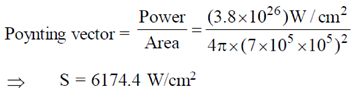

46. Unpolarized light is incident on a calcite plate at an angle of incidence 50º, as shown in the figure. Take n₀ = 1.6584 and n_e = 1.4864 for calcite. The angular separation (in degrees) between the two emerging rays within the plate is ___________

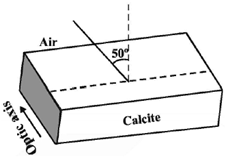
Ans. (3.51°)

Sol. The light is travelling in the perpendicular direction to the optic axis, so the refraction indices for ordinary and extraordinary rays are independent of angle of incident.

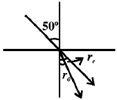
We have,

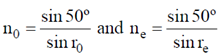
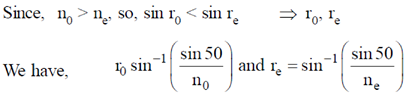
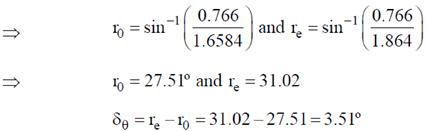
47. A rod is moving with a speed of 0.8c in a direction at 60º to its own length. The percentage concentration in the length of the rod is ________

Ans. (8.3)

Sol. Since the rod is along x-axis

Therefore, only x-component of velocity will make a significant effect on the length of the rod.

Apparent length of the rod

 

 

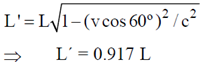
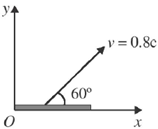
Percentage contraction in length

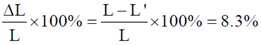
48.

Ans. (1.3)

Sol. Given the state of the particle

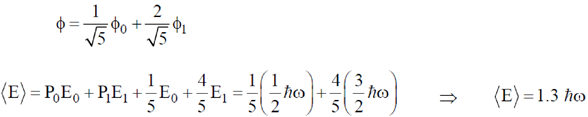
49. In the given circuit, V_CC = 10V and = 100 for the n-p-n transistor. The collector voltage V_C (in volts) is ___________

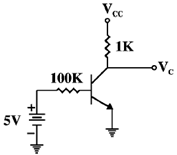
Ans. (5.7 or 5V)

Sol. If V_BE = 0.7 V

–5 + I_B.100k + 0.7 = 0 V_BE = 0

V_C = V_CC – I_CR_C V_C = 10 – 5 mA × 1k = 5V

V_C = 10 – 4.3 mA × 1k = 5.7 V

50. In the hydrogen atom spectrum, the ratio of the longest wavelength in the Lyman series (final state n = 1) to that in the Balmer series (final state n = 2) is ___________.

Ans. (0.185)

Sol. Longest wavelength in Lymann series corresponds to n = 2 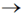n = 1

Longest wavelength in Balmer series corresponds to n = 3 n = 2

51. A plane electromagnetic wave of frequency 5 × 10¹⁴ Hz and amplitude 10³ V/m, travelling in a homogeneous dielectric medium if dielectric constant 1.69, is incident normally at the interface with a second dielectric medium of dielectric constant 2.25. The ratio of the amplitude of the transmitted wave to that of the incident wave is __________

Ans. (0.92857)

Sol. The refractive index of first medium

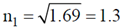
And refractive index of second medium

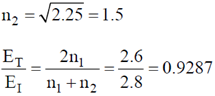
52. For the arrangement given in the following figure, the coherent light source A, B and C have individual intensities of 2 mW/m², 2 mW/m² and 2 mW/m², respectively at point P. The wavelength of each of the sources is 600 nm. The resultant intensity at point P (in mW/m²) is _____________

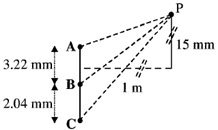
Ans. (5)

Sol. In the Young's double slit arrangement, the path difference,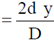

Where, 2d = distance between slits

D = distance between slits and screen

y = distance of the point P from the central bright fringe.

The path difference between the rays from A and B = 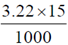= 0.04830 mm = 48300 nm

Now,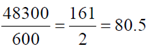

So the path difference is the odd multiple of 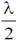and these wave interfere destructivity. Both sources i.e. A and B have the same intensities (same amplitude). So, the resultant intensity due to A and B at P is zero.

We can conclude here that the intensity at P is only due to C i.e. 5 mW/m²

Correct answer is (5 mW/m²).

53. In a region of space, a time dependent magnetic field B(t) = 0.4t Tesla points vertically upwards. Consider a horizontal, circular loop of radius 2 cm in this region. The magnitude of the electric field (in mV/m) induced in the loop is ____________

Ans. (4)

Sol.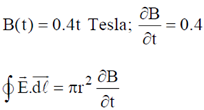

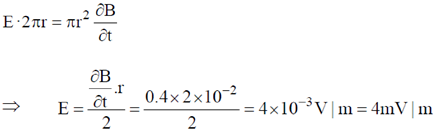
54. A homogeneous semi-circular plate of radius R = 3m is shown in the figure. The distance of the center of mass of the plate (in meter) from the point O is _____________

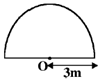
Ans. (1.273)

Sol.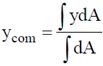

55. A uniform disk of mass m and radius R rolls, without slipping down a fixed plane inclined at an angle 30º to the horizontal. The linear acceleration of the disk (in m/sec²) is _______________

Ans. (3.267)

Sol. Linear acceleration

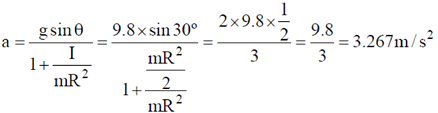
56. In the thermodynamic cycle shown in the figure, one mole of a monatomic ideal gas is taken through a cycle. AB is a reversible isothermal expansion at a temperature of 800 K in which the volume of the gas is doubled. BC is an isobaric contraction to the original volume in which the temperature is reduced to 300 K. CA is a constant volume process in which the pressure and temperature return to their initial values. The net amount of heat (in joules) absorbed by the gas in one complete cycle is ________

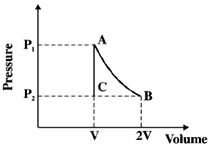
Ans. (452.28)

Sol. For complete cycle,

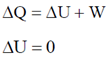
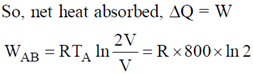
W_BC = P₂(V_C – V_B) = RT_C – RT_B = R(300 – 800) = –500R

W_CA = 0

So, W = W_AB+W_BC+W_CA = R × 800 ln 2 – 500 R= R[800 ln 2 – 500]= 452.28 J

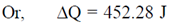
57. A nozzle is in the shape of a truncated cone, as shown in the figure. The area at the wide end is 25 cm² and the narrow end has an area of 1 cm². Water enters the wider end at a rate of 500 gm/sec. The height of the nozzle is 50 cm and it is kept vertical with the wider end at the bottom. The magnitude of the pressure difference in kPa (1 kPa = 10³ N/m²) between the two ends of the nozzle is _______

Ans. (17.48)

Sol. Given

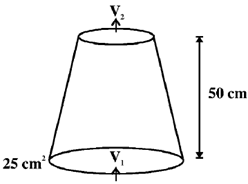
Equation continuity

V₁A₁ = V₂A₂

20 × 25 = V₂ × 1

V₂ = 500 cm/sec

Bernoulis theorem

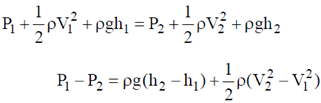
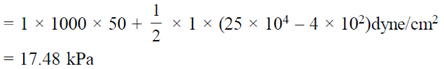
58. One gram of ice at 0ºC is melted and heated to water at 39ºC. Assume that the specific heat remains constant over the entire process. The latent heat of fusion of ice is 80 Calories/gm. The entropy change in the process (in Calories per degree) is ___________

Ans. (0.427)

Sol.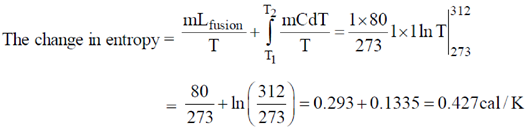

59. A block of mass 2 kg is at rest on a horizontal table. The coefficient of friction between the block and the table is 0.1. A horizontal force 3 N is applied to the block. The speed of the block (in m/s) after it has moved a distance 10 m is ___________

Ans. (3.162)

Sol.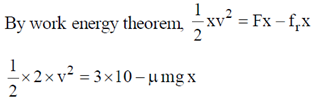

v² = 30 – 0.1 × 2 × 10 × 10

= 30 – 20

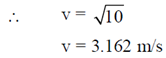
60. Consider a 20 µm diameter p-n junction fabricated in silicon. The donor density is 10¹⁶ per cm³. The charge developed on the n-side is 1.6 × 10^–13 C. Then the width (in µm) of the depletion region on the n-side of the p-n junction is _________

Ans. (0.32)

Sol. Charge developed on n-side