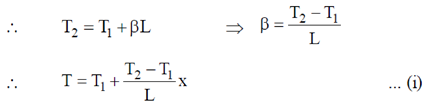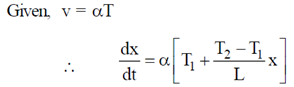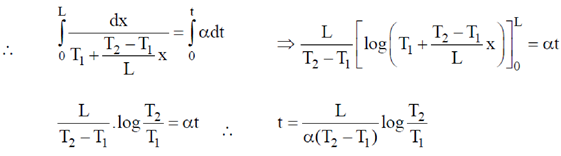1. The inverse of the matrix

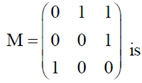
(a) M – I

(b) M² – I

(c) I – M²

(d) I – M

Where I is the identity matrix.

Ans. (b)

Sol. Let 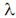be eigen value of the matrix.

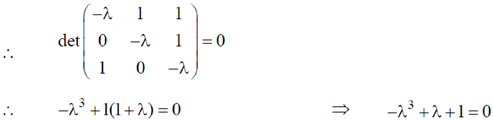
Using caley Hamilton theorem we get, –M³ + M + I = 0

If M^–1 be inverse of M. Multiplying above equation by M^–1 we get

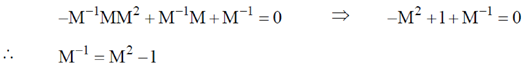
2.

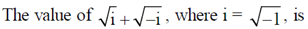
(a) 0

(b)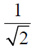

(c)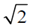

(d)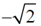

Ans. (c)

Sol.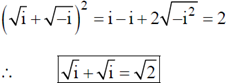

3. A particle is released at x = 1 in a force field 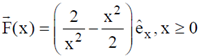. Which one of the following statements is FALSE?

(a) 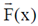is conservative

(b) The angular momentum of the particle about the origin is constant.

(c) The particle moves towards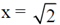

(d) The particle moves towards the origin.

Ans. (d)

Sol.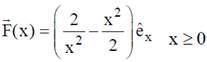

Force is directed along x-axis.

 

 

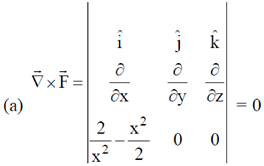
This implies that is conservative.

(b) passes through origin, therefore torque due to about O is zero. Therefore, angular momentum about origin is conserved.

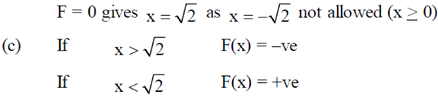
This implies that force is always directed towards 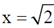. Therefore particle moves towards .

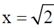Therefore, statement of last option that particle moves towards origin is false.

4. A travelling pulse is given by f(x,t) = A exp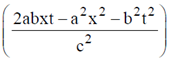, where A, a, b and c are positive constants of appropriate dimensions. The speed of the pulse is

(a)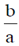

(b)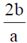

(c)

(d)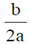

Ans. (a)

Sol. A travelling pulse is given by

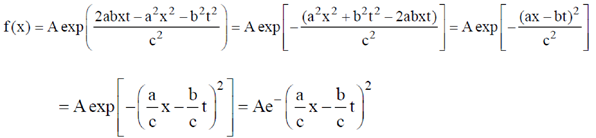
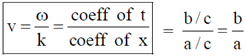
5. If the dimensions of mass, length, time and charge are M, L, T and C respectively, the dimensions of the magnetic induction field 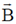is

(a) ML²T^–1C^–1

(b) MT^–1C^–1

(c) L²T^–1C

(d) L^–1T^–1C

Ans. (b)

Sol. Using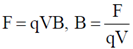

Dimension of F = [M L T^–2], Dimension of velocity V = [L T^–1]

Dimension of charge q = [C]

Therefore, dimension of magnetic induction field

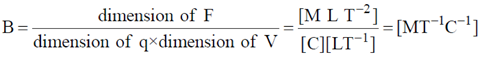
6. A blackbody at temperature T emits radiation at a peak wavelength 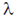. If the temperature of the blackbody becomes 4T, the new peak wavelength is

(a)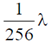

(b)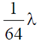

(c)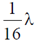

(d)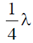

Ans. (d)

Sol. According to Wien's displacement law

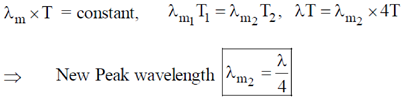
7. Let N_MB, N_FD denote the number of ways in which two particles can be distributed in two energy states according to Maxwell-Boltzmann, Bose-Einstein and Fermi-Dirac statistics respectively. Then: N_MB : N_BE : N_FD is:

(a) 4 : 3 : 1

(b) 4 : 2 : 3

(c) 4 : 3 : 3

(d) 4 : 3 : 2

Ans. (a)

Sol. MB statistics applies to the system to distinguishable particles, (consider A and B) two particles can be distributed in four ways in two energy states.

BE statistics applies to system of indistinguishable particles not obeying Pauli's exclusion principal.

Therefore according to this statistics the number of ways N_BE in which two particles can be distributed in two energy states is 3. Consider two particle A and A.

N_BE = 3

and FD statistics applies to indistinguishable particles obeying Pauli's exclusion principles.

Therefore, N_FD = 1

8. Electric field component of an electromagnetic radiation varies with time as E = a(cos t + sin t cos 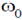t), where a is a constant and the values of 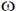and 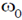are 1 × 10¹⁵ s^–1 and 5 × 10¹⁵ s^–1, respectively. This radiation falls on a metal of work function 2 eV. The maximum kinetic energy in (eV) of photoelectrons is:

(a) 0.64

(b) 1.30

(c) 1.70

(d) 1.95

Ans. (d)

Sol.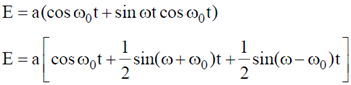

For maximum kinetic energy,

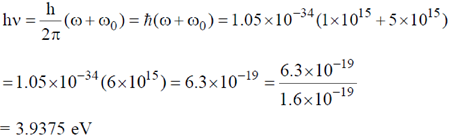
Now according to Einstein, the photoelectric effect in a given metal should obey the equation

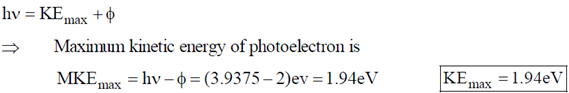
9. The fraction of volume unoccupied in the unit cell of the body centered cubic lattice is

(a)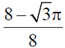

(b)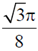

(c)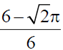

(d)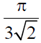

Ans. (a)

Sol. In the unit cell of the body centred cubic lattice

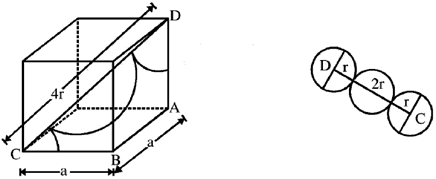
a is the lattice constant. Coordination number 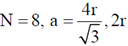is the nearest neighbour distance number of atoms per unit cell

 

 

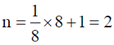
Volume of all the atoms in a unit cell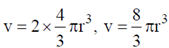

and volume of the unit cell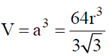

Therefore, unoccupied volume =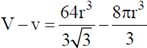

and the fraction of volume unoccupied unit cell of body centred cubic lattice

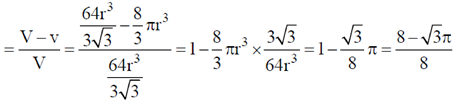
10. For an ideal op-amp circuit given below, the dc gain and the cut off frequency, respectively are

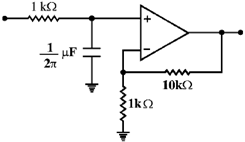
(a) 1 and 1 kHz

(b) 1 and 100 Hz

(c) 11 and 1 kHz

(d) 11 and 100 Hz

Ans. (c)

Sol.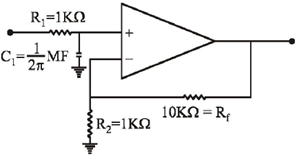

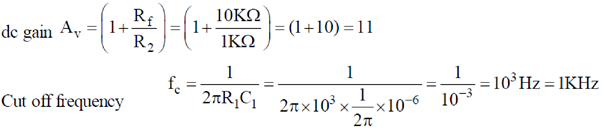
11. The solution of the differential equation dz(x, y) + xz(x, y) dx + yz (x, y)dy = 0 is _________

Sol. dz(x, y) = –z(x, y) [xdx + ydy]

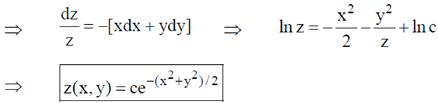
12. Given that f(1) = 1, f ´(1) = 1 and f ´´(1) = 1, the value of f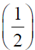is ________

Sol. Given f(1) = 1, f´(1) = 1, f´´(1) = 1

Using Taylor Series

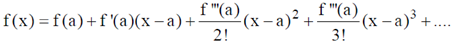
Taking a = 1 and 3 terms of it

 

 

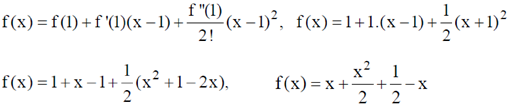
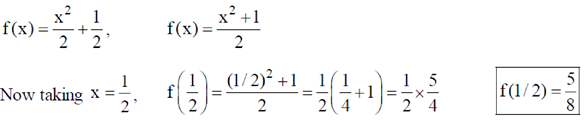
13. Two tubes A and B are connected through another tube C. A mercury manometer is connected between B and C (see figure). The diameter of B and C are 0.04 m and 0.01 m, respectively. An incompressible fluid of density 1.0 × 10³ k gm^–3 enters A, and leaves B with a constant speed 0.2 ms^–1. If the density of mercury is 13.6 × 10³ k gm^–3, the height 'h' of the mercury column in the manometer is _______

(Take acceleration due to gravity g = 10 ms^–2)

Sol. Given arrangement is actually a venturi meter

Given speed of the fluid in tube B, V_B = 0.2 m/s

Diameter of Tube B = 0.04 m, It's radius r_B = 0.02 m, Diameter of Tube C = 0.01m

It's radius r_C = 0.005 m

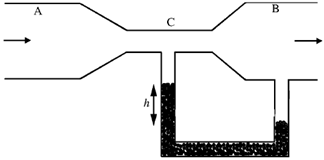
According to the continuity equation for incompressible fluid

AV = constant, A = Area, V = velocity

A_CV_C = A_BV_B

 

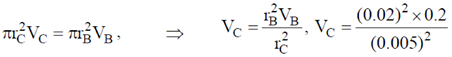
V_C = 3.2 m/s

Pressure drop, indicated by the manometer

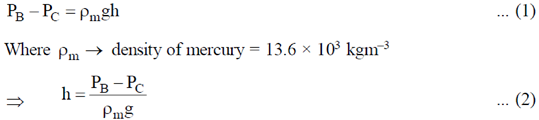
To find P₁ – P₂, we can use Bernoulli's principle

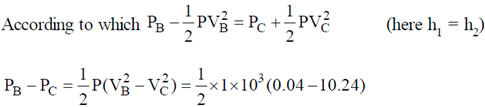
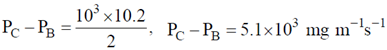
Now substituting this value in equation (2)

Magnitude of height h of the mercury column in the manometer is given by

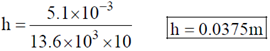
14. The path of a particle of mass 'm', moving under the influence of a central force, in plane polar coordinates is given by r = 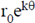, where r₀ and k are positive constants of appropriate dimensions. The angular momentum of the particle is L and its total energy is zero. The potential energy function V(r), in terms of m, L and k is __________

Sol. Angular momentum in central force motion (planar motion) is given as

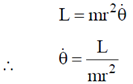
Kinetic energy of particle is given as

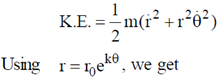
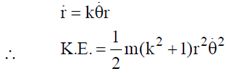
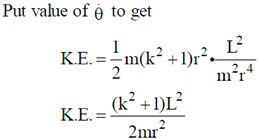
Given, T.E. = 0

P.E. + K.E. = 0

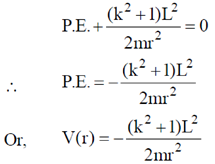
15. The dimensions of a thin convex lens of refractive index n are shown in the figure. The radius of curvature of the lens in terms of n, h and 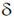(where, << h) is _______________

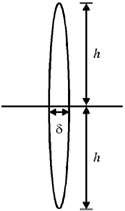
Sol. Consider a parallel beam of light incident on the lens. Let it undergoes a deviation of

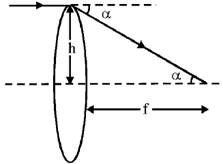
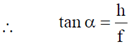
If 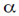is small (which true for thin lenses)

Upper half of the lens can be approximately considered as a prism of vertex angle

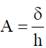
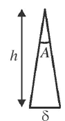
We know that a light ray passing through a prism undergoes a deviation of A(n – 1)

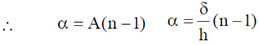
Comparing with (i), we get

For a thin biconvex lens using lens-maker formula we get,

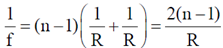
Using equation (ii), we get

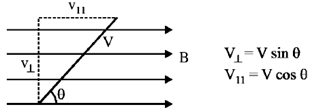
16. A charged particle of mass m, charge q and constant velocity enters a uniform magnetic field 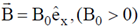, at an angle 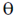to the direction of magnetic field. Find the angle 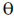, if in one revolution of the helical motion, the particle advances along the direction of the magnetic field a distance equal to the radius of the helical path. _____________

Sol. If a charge particle of mass m, charge q and constant velocity v enters a uniform magnetic field 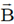, at an angle 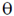to the direction of magnetic field, its motion is along a helical path with axis of helix being the field direction. The radius of this path is given by 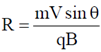and pitch of the helix, which is actually the distance covered by e^– along the field direction in one revolution.

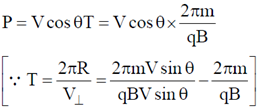
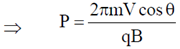
Given, Pitch of the helix = Radius of helical path

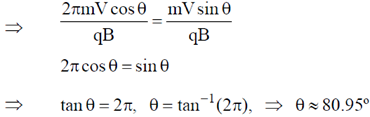
17. Two thermally isolated identical systems have heat capacities which vary as C_V = 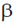T³ (where 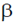> 0). Initially one system is at 300 K and the other at 400 K. The systems are then brought into thermal contact and the combined system is allowed to reach thermal equilibrium. The final temperature of the combined system is _________

Sol. Let T = temperature of combined system. Therefore using principle of calorimetry we get,

heat lost = heat gained.

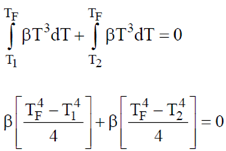
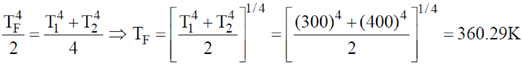
18. A beam of X-rays of wavelength 0.2 nm is incident on a free electron and gets scattered in a direction with respect to the direction of the incident radiation resulting in maximum wavelength shift. The percentage energy loss of the incident radiation is __________

Sol. Loss in energy of incident radiation

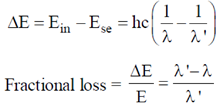
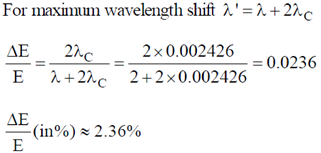
19. A free particle of mass 'm' is confined to a region of length L. The de-Broglie wave associated with the particle is sinusoidal in nature as given in the figure. The energy of the particle is _________

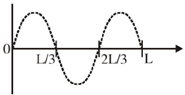
Sol.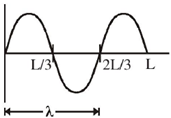

This is 2nd excited state (n = 3) of the particle because it has 2 nodes.

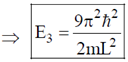
20. A variable power supply (5V-20V) is connected to a Zener diode specified by a breakdown voltage of 10V (see figure). The ratio of the maximum power to the minimum power dissipated across the load resistor is ______

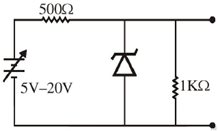
Sol.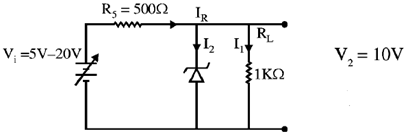

 

To check the status of zener diode (ON or OFF)

For V = 20 V

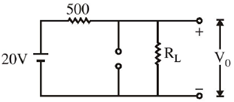
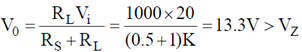
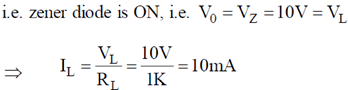
than maximum power dissipation across load resistor is

P_max = V₂L₂ = 10 × 10 × 10^–3 = 100 mW

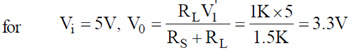
here V₀ < V₂

The zener diode is OFF

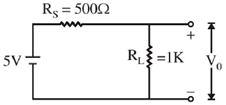
Min power dissipation across load resistor P_min = I² × R_L =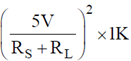

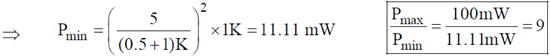
21. Apply Gauss divergence theorem to the gravitational field due to spherical object of mass M and uniform density 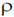located at the origin. Obtain Gauss's law for gravitation (analogous to the Gauss law in electrostatics) in integral and differential forms.

Sol.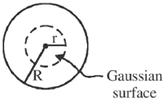

Consider an insider point at a distance r < R from centre.

Gravitational field at this point is,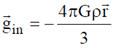

Therefore, flux of 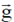through a sphere of radius 'r' is

 

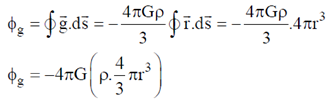
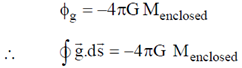
For outside point: Gravitational field at a distance r > R from centre of a sphere is given as

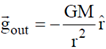
Therefore, flux through a surface of radius 'r' is

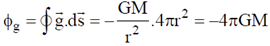
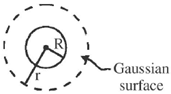
In this case sphere is completely enclosed enclosed by the Gaussian surface

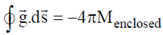
Therefore, in general for any point we can write for gravitational field

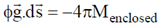
Using Gauss's div theorem we get, 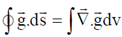and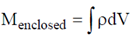

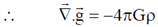
22. A thin annular disc of inner and outer radii a and b (a < b) respectively has uniform mass density s_s and is placed in the soy-plane such that its axis lies along the z-axis. Determine the gravitational force due to the disc on a particle of mass 'm' located on the z-axis at a distance z from the origin. If the particle is released at z, such that z << a, b, describe the nature of motion of the particle.

Sol. Consider an elementary part of the disc: Take it to be a thin ring of radius 'r' and thickness 'dr' as shown in the figure.

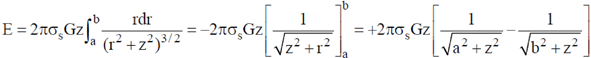
Therefore, gravitational force,

 

 

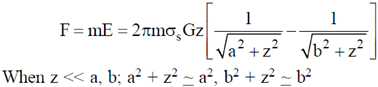
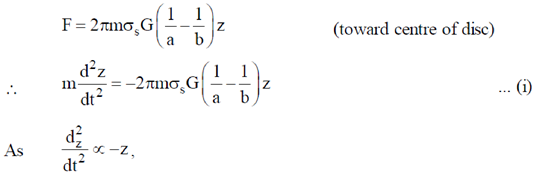
Therefore, particle will undergo S.H.M. and frequency of oscillation is obtained by comparing equation (i) to standard equation of S.H.M.

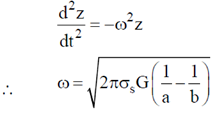
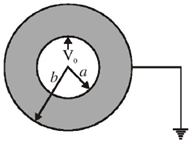
23. A concentric spherical volume of inner radius 'a' and outer radius 'a' and outer radius 'b' is filled with a material of finite conductivity specified by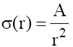

where A is a positive constant of appropriate dimensions. The outer surface is grounded and the inner surface is maintained at a potential V₀. Calculate the resistasnce of this configuration.

Sol. We know that resistance of a conductor is given as

Where l = length or spacing between cross section through which current flows.

A = area of cross section. In the present problem area of cross section is not constant.

Therefore, we first calculate resistance of elementary part and then integrate it to get total resistance. The flow of current is shown by dotted arrow.

Therefore, for elementary part (which is a shell of radius 'r' and thickness 'dr'). Resistance is given as

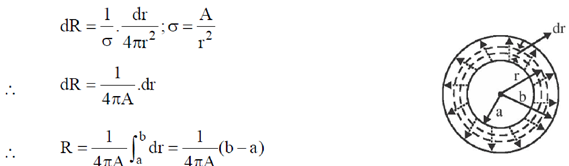
24. A conducting solid sphere of radius a, carrying a charge q is kept in a dielectric of dielectric constant k, such that half the sphere is surrounded by the dielectric as shown in figure. Find the surface charge densities in the upper and lower hemispherical surfaces.

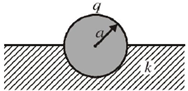
Sol. Let us assume that charge on upper half is q₁ and that on lower half is q₂.

and field lines are shown in the figure.

We know that parallel components of E vector at the boundary of two media is same. Therefore,

E₁ = E₂ ... (ii)

To get E₁ = E₂ we first calculate D₁ and D₂. We draw Gaussian surface as shown in the figure dotted line. Inside metal D = 0.

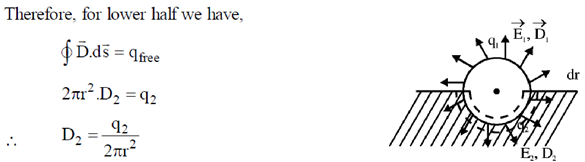
Similarly, for upper half we get,

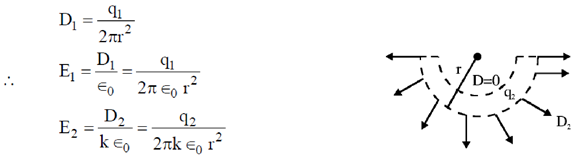
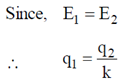
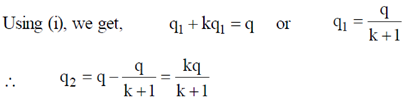
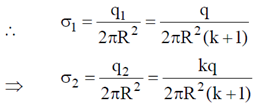
25. A particle of mass 'm' is subjected to a potential V(x) = ax², –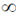 < x < 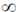, where 'a' is a potive constant of appropriate dimensions. Using the relation 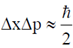, estimate the minimum energy of the particle.

Sol. Let x = displacement from mean position

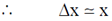
Using Heisenberg uncertainty relation we get,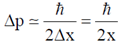

Therefore, minimum energy is

 

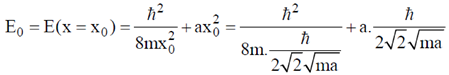
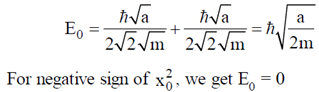
26. A hollow cylinder (closed at both ends) with adiabatic walls is divided into 'n' equal cells (C₁, C₂, ....... C_n) using discs D₁, D₂, ........ D_n–1 (see figure). The discs can slide freely without friction. The first disc (D₁) is adiabatic and the remaining discs are diathermal (thermally conducting). Each cell contains one mole of ideal monoatomic gas. Let the initial pressure, volume and temperature of each cell be P₀, V₀ and T₀ respectively. The gas in cell C₁ (first cell) is heated slowly until the temperature of the gas in cell C_n (last cell) reaches final equilibrium temperature 4T₀. Find the volume of the first cell in terms of the number of cells (n) and the initial volume (V₀).

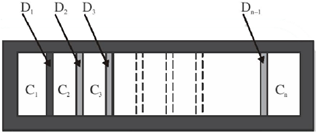
Sol. Process is slow, and discs D₂, D₃....D_n-1 are conducting. Therefore, when temperature of c_n reaches 4T₀

Temperature of chambers c₂, c₃, ..... c_n–1 also becomes 4T₀. Therefore, chambers c₂, c₃, .... c_n can be considered as a single chamber of initial volume (n –1) V₀.

We have following situation,

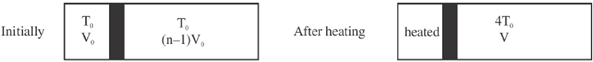
When gas on the left is heated gas on the right undergoes adiabatic process.

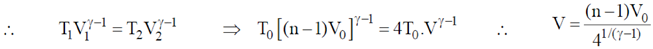
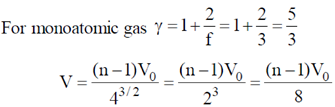
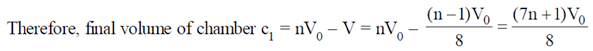
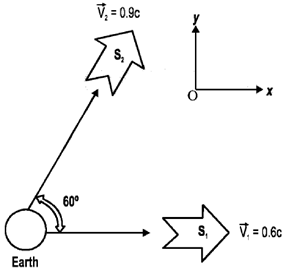
27. A spaceship S₁ leaves the Earth along the positive x-direction. Another spaceship S₂ also leaves the earth along the direction which makes an angle 60º with x-axis. The speeds of S₁ and S₂ are measured by 0.6c and 0.9c respectively by an observer on the Earth. Find the speed of S₂ as measured by an observer in S₁.

Sol. Speed of S₂ as measured in S₁ is given as

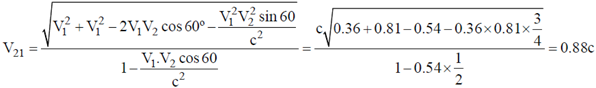
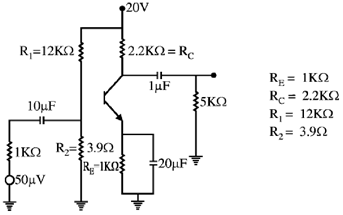
28. For the given circuit, calculate the input impendance, output impedance and voltage gain.

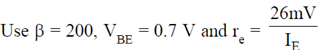
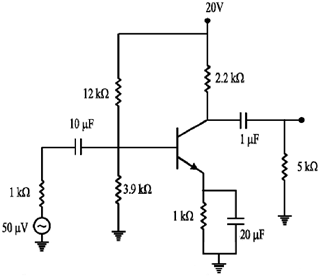
Sol.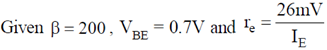

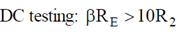
200 × 1K > 10 × 3.9K, 200 K > 39K (Satisfied)

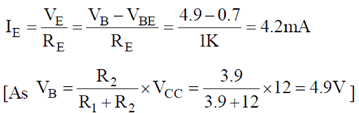
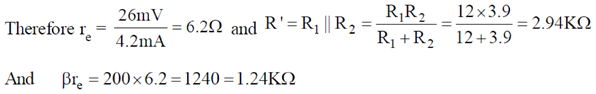
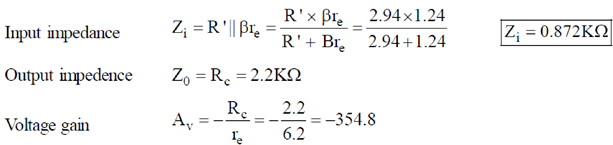
29. The mass density of a disc of mass 'm' and radius R varies as

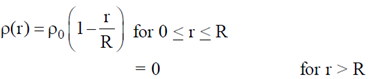
Find the moment of inertia of the disc about the axis perpendicular to the plane of the disc and passing through the centre of the disc in terms of m and R.

Sol. We can determine the moment of inertia of a disc by breaking a disc into many rings.

 

 

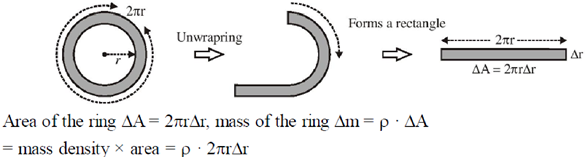
As we allow the number of rings to approach infinity the differential 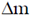becomes dm, 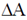becomes dA while the differential 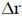becomes dr.

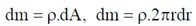
therefore the total mass of the disc

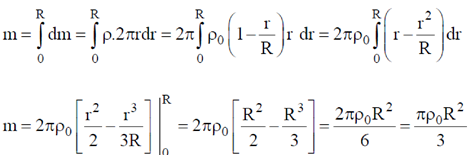
The moment of inertia of the disc.

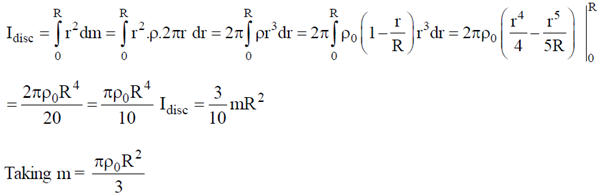
This is the required moment of inertia of the disc about the axis perpendicular to the plane of the disc and passing through the centre of disc in terms of m and R.

30. The speed of sound propagation in air as a function of temperature T is given by v = 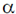T, where 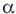is a constant of appropriate dimensions. Calculate the time taken for a sound wave to travel a distance L between two points A and B, if the air temperature between the points varies linearly from T₁ to T₂.

Sol. It is given that air temperature varies linearly. Therefore, we can assume that at a distance 'x' from A temperature is given as

At A, x = 0, T = T₁

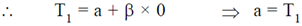
At B, x = L, T = T₂