PYQ 2015 - VedPrep

IIT JAM MATHEMATICS - 2015
Previous Year Question Paper with Solution.

1. Suppose N is a normal subgroup of a group G. Which one of the following is true?

(a) If G is an infinite group then G/N is an infinite group.

(b) If G is a non-abelian group then G/N is a non-abelian group.

(d) If G is an abelian group then G/N is a cyclic group.

Ans. (c)

Sol.

Option (c) is correct.

2. The volume of the portion of the solid cylinder x² + y² < 2 bounded above by the surface z = x² + y² and bounded below by the xy-plane is

(a)

(b)

(c)

(d)

Ans. (b)

Sol.

Option (b) is correct.

3. Let S be a non-empty subset of R. If S is a finite union of disjoint bounded intervals then which one of the following is true?

(a) If S is not compact, then

(b) Even if sup S need not be compact.

(d) Even if S is compact, it is not necessary that sup

Ans. (b)

Sol.

but S is not closed, hence not compact

Option (b) is correct.

4. Let {x_n} be a convergent sequence of real numbers. If for n > 1 then which one of the following is the limit of this sequence?

(a)

(b)

(c)

(d)

Ans. (a)

Sol.

Option (a) is correct.

5. Let a, b, c, d be distinct non–zero real numbers with a + b = c + d. Then an eigenvalue of the matrix is

(a) a + c

(b) a + b

(d) b – d

Ans. (b)

Sol.

Option (b) is correct.

6. Let A be a non-empty subset of R. Let I(A) denote the set of interior points of A. Then I(A) can be

(a) empty

(b) singleton

(d) countable but not finite

Ans. (c)

Sol. Set of interior points of any subset of R is always uncountably infinite or empty. To support the option (a), we can take example, A = {1, 2, 3}. Clearly, I(A) =

Option (c) is correct.

7. Let y(x) = u(x) sin x + v(x) cos x be a solution of the differential equation Then u(x) is

(a) ln|cos x| + C

(b) –x + C

(d) ln|sec x| + C

Ans. (c)

Sol. Let y₁(x) = sin x, y₂(x) = cos x y₁, y₂ are solutions of

By the method of variation of parameters solution of is

y = y₁ (x) u(x) + y₂ v(x) = u(x) sin x + v(x) cos x

Option (c) is correct.

8. An integrating factor of the differential equation is

(a)

(b)

(d) y²

Ans. (c)

Sol.

Let y^a be an integrating factor.

Option (c) is correct.

9. Let be a differentiable function with f(0) = 0. If for all , then which one of the following statements is true on

(a) f is unbounded

(b) f is increasing and bounded

(d) f is periodic

Ans. (a)

Sol.

x and 2x both go

Option (a) is correct.

10. If an integral curve of the differential equation passes through (0, 0) and is equal to

(a) 2 – e^–1

(b) 1 – e^–1

(d) 1 + e

Ans. (c)

Sol.

It is a linear differential equation in x. Its integrating factor IF = e^y.

Hence

It passes through (0, 0). Therefore, c = 1. Thus, solution is x = y –1 + e^–y.

It passes through

Option (c) is correct.

11. Let S be the bounded surface of the cylinder x² + y² = 1 cut by the planes z = 0 and z = 1 + x. Then the value of the surface integral is equal to

(a)

(b)

(c)

(d)

Ans. (a)

Sol.

Option (a) is correct.

12. Let be the vector space of polynomials in x of degree at most 2 with real coefficients. Let be the vector space of 2 × 2 real matrices. If a linear transformation is defined as

T(f) =

then

(a) T is one-one but not onto

(b) T is onto but not one-one

(d) Null (T) = span{x² – 2x 1 – x}

Ans. (c)

Sol. Let f(x) = a₀ + a₁x + a₂x². f (0) = a₀, f(1) = a₀ + a_l + a₂, f (2) = a₀ + 2a_l + 4a₂.

Hence, Range (T) = .

Option (c) is correct.

13. Let S = . Which one of the following statements is false?

(a) There exists sequences {a_n] and {b_n] in [0, 1] such that S =

(b) [0,1]\S is an open set.

(d) There exists an infinite subset of S having no limit points

Ans. (d)

Sol.

Which is an open set. Hence (a) and (b) are true. An infinite subset of S must contain limit in an interval or if countably infinite then it must have limit point in any one of the intervals

Option (d) is correct.

14. The limit

(a) 0

(b)

(c)

(d)

Ans. (d)

Sol.

Option (d) is correct.

15. Let S₃ be the group of permutations of three distinct symbols. The direct sum has an element of order

(a) 4

(b) 6

(d) 18

Ans. (b)

Sol. S₃ = {(1), (12), (23), (31), (123), (132)}.

O(1) = 1, O((12)) = O((23)) = O((31)) = 2, O((123)) = O((132)) = 3.

Option (b) is correct.

16. Let B₁ = {(1, 2), (2, – 1} and B₂ = {(1, 0), (0,1)} be ordered bases of R². If is a linear transformation such that [T]B₁, B₂, the matrix of T with respect to B₁ and B₂ is then T(5, 5) is equal to

(a) (–9, 8)

(b) (9, 8)

(d) (15, 2)

Ans. (d)

Sol.

B₂ is the standard bases of R². Hence, [T(5, 5)]_B2 = T(5, 5) = (15, 2).

Option (d) is correct.

17. Let G be a non-abelian group. Let have order 4 and let have order 3. Then the order of the element in G

(a) is 6

(b) is 12

(d) need not be finite

Ans. (d)

Sol. For a non-abelian group, say H, if x and y belonging to H having orders 4 and 3 respectively, then order of xy is 12 and any index of xy having integral multiple of 12 gives the result identity. But, this does not seem to be true for an abelian group. So, for identity e = n may be finite or infinite.

Option (d) is correct.

18. Let A =

(a) an eigenvalue of B is purely imaginary

(b) an eigenvalue of A is zero

(d) A has a non-zero real eigenvalue

Ans. (c)

Sol.

Option (c) is correct.

19. Suppose that the dependent variables z and w are functions of the independent variables x and y defined by the equations f(x, y, z, w) = 0 and g(x, y, z, w) = 0 where f_zg_w – f_wg_z = 1. Which one of the following is correct?

(a) z_xf_wg_x × f_xg_w

(b) z_x = f_xg_w – f_wg_x

(d) z_x = f_zg_w – f_zg_x

Ans. (a)

Sol.

From g_w(1) – f_w(2).

[f_xg_w g_xf_w) z_x (f_zg_w g_zf_w) = 0.

Option (a) is correct.

20. The orthogonal trajectories of the family of curves y = C₁x³ are

(a) 2x² + 3y² = C²

(b) 3x² + y² = C²

(d) x² + 3y² = C²

Ans. (b)

Sol.

Option (b) is correct.

21. Which one of the following statements is true for the series

(a) The series converges conditionally but not absolutely.

(b) The series converges absolutely.

(d) The sequence of partial sums of the series is unbounded.

Ans. (b)

Sol. By ratio test

So, the series converges absolutely.

Option (b) is correct.

22. Let G and H be nonempty subsets of R where G is connected and is not connected. Which one of the following statements is true for all such G and H?

(a)

(b)

(c)

(d)

Ans. (d)

Sol. Take, G = (1, 2) and Then, is not connected and H is not connected. So, this rules out (a).

Take, G = (1, 2) and H = (3, 4). Then, is not connected but H is connected. So, this rules out (b).

Take, G = (1, 3) and is not connected and H is also not connected. So, this rules out (c).

If G is connected and if H is connected then must be connected which is a contradiction. Hence, H must be disconnected. So, correct option is (d).

Option (d) is correct.

23.

Then at x = 0, f_{m, n} is

(a) differentiable for each pair m, n with m > n.

(b) differentiable for each pair m, n with m < n.

(d) not differentiable for each pair m, n with m < n.

Ans. (a)

Sol.

Option (a) is correct.

24. For what real values of x and y does the integral attain its maximum?

(a) x = –3, y = 2

(b) x = 2, y = 3

(d) x = –3, y = 4

Ans. (a)

Sol.

f_x(x, y) = –6 + x + x²; f(x, y) = 6 – y – y²

f_xx(x, y) = 1 + 2x; f_yy(x, y) = –1 – 2y; f_xy(x, y) = 0

f_x(x, y) = fy(x, y) = 0 for x = 2, –3, y = 2, –3.

Critical points are (2, 2), (2, –3), (–3, 2), (–3, 3).

So, only possible solution among the given options is x = –3, y = 2.

Discriminant, D(x, y) = f_xxf_yy – f²_xy; D(–3, 2) = (1 + 2x) (–1 – 2y) = (–5) (–5) = 25 > 0.

f_xx (–3, 2) = 1 – 6 = – 5 < 0.

So, f has max. at (–3, 2).

Option (a) is correct.

25. be given by

f(x, y) =

Then the value of g(x, y) =

(a) changes with x but not with y

(b) changes with y but not with x

(d) neither changes with x nor with y

Ans. (d)

Sol.

So, f is a homogeneous function of degree –1.

Therefore, xf_x + yf_y = (–1)f.

is constant so neither changes w.r.t. x or y.

Option (d) is correct.

26. Let be a strictly increasing continuous functions. If {a_n} is a sequence in [0, 1] then the sequence {f(a_n)} is

(a) increasing

(b) bounded

(d) not necessarily bounded

Ans. (b)

Sol. [0, 1] is a compact subset of R and f is continuous on R.

So, f is continuous on [0, 1]. So, f is bounded on [0, 1].

Option (b) is correct.

27. The area of the planar region bounded by the curves x = 6y² – 2 and x = 2y² is

(a)

(b)

(c)

(d)

Ans. (c)

Sol. Solving the two curves: x = 2y² and x = 6y² – 2, 2y² = 6y2 – 2

Option (c) is correct.

28. If y(t) is a solution of the differential equation is equal to

(a)

(b)

(c)

(d)

Ans. (b)

Sol.

Option (b) is correct.

29. The sequence is

(a) monotone and convergent

(b) monotone but not convergent

(d) convergent but not monotone

Ans. (a)

Sol.

is an increasing function which varies within .

So of that is decreasing hence monotone.

Option (a) is correct.

30. For be given by f_n(x) = xⁿ sin x. Then at x = 0, f_n has a

(a) local maximum if n is even

(b) local maximum if n is odd

(d) local minimum if n is odd

Ans. (d)

Sol.

While passing through x = 0, cos x and n doesn't change sign changes sign from negative to positive.

So, for 'n' being odd, x^{n – 1} doesn't change sign.

Hence f_n(x) changes sign from negative to positive and f_n(x) is continuous.

So, by the test of first derivative f_n has a minimum at x = 0 if n is odd.

Option (d) is correct.

31. Let be defined by f(x, y) = .

At (0, 0)

(a) f is not continuous

(b) f is continuous and both f_x and f_y exist

(d) f_x and f_y exist but f is not differentiable

Ans. (b), (c)

Sol.

= 0 = f(0, 0)

f is continuous at (0, 0).

Existence of limit can also be shown by using definition and changing to polar coordinates.

But, the limit is very obvious.

f is differentiable at (0, 0).

Option (b), (c) are correct.

32. Let be a function defined by f(x) = In which of the following interval(s), f takes the value I?

(a) [–6, 0]

(b) [–2, 4]

(d) [6, 12]

Ans. (a), (b), (d)

Sol.

Hence, f takes the value 1 in the intervals [–6, 0], [2, 8] and [6, 12] by mean value theorem.

Option (a), (b), (d) are correct.

33. Let be functions. Let R(f) and R(g) be the ranges of f and g, respectively. Which of the following statements is/are true?

(a)

(b)

(c)

(d)

Ans. (b), (c), (d)

Sol. For the graph of f and g may be as shown in the figure. Here both graphs may also touch. From the diagram, we can say inf R(f) < sup R(g), but we can't say sup R(f) < inf R(g) (as seen in the graph).

For f (x) < g(y), for all x, y [0,1], max. f < min g on [0, 1] = sup( f) < inf R(g). So, (d) is correct.

Option (b), (c), (d) are correct.

34. Let be the function defined by Then

(a) f is decreasing in (–1, 0)

(b) f is increasing in (0, 1)

(d) f(x) = 1 has no solutions in (–1, 1)

Ans. (a), (b), (c)

Sol.

Clearly, for 0 < x < 1 and for –1 < x < 0. So, f (x) has minimum at x = 0. So, f (x) is decreasing in (–1, 0) and increasing in (0, 1).

f(0) = 0. Hence, f(x) = 1 has exactly one solution in each of the intervals (–1, 0) and (0, 1). Hence, (c) is a correct answer.

Option (a), (b), (c) are correct.

35. Which of the following conditions implies/imply the convergence of a sequence {x_n} of real numbers?

(a)

(b)

(c)

(d)

Ans. (d)

Sol. Take the example

Clearly, for any there exists an such that for all

But {x_n} does not converge. So, (a) is incorrect.

Similarly, choosing the example x_n =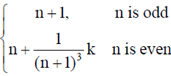

We can say that (c) is incorrect.

(b) requires weaker conditions than (a). So (b) is also incorrect.

(d) is Cauchy criteria for convergence of sequence, so it is correct.

Option (d) is correct.

36. Which of the following statements is/are true on the interval ?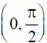

(a) cos x < cos(sin x)

(b) tan x < x

(c)

(d)

Ans. (d)

Sol. x > sin x on and cos x is decreasing on

So, (a) is correct.

(b) is incorrect as can be seen from the graphs of y = x and y = tan x.

From graph-1 (c) is true.

From the graph-1, (c) is not true.

is a decreasing function and ln(2 + x) is increasing on .

Hence, 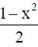< ln(2 + x) (refer graph 2).

Option (d) is correct.

37. Which of the following statements is/are true?

(a)

(b)

(c)

(d)

Ans. (a), (c)

Sol.

Option (a), (c) are correct.

38. The initial value problem has

(a)

(b)

(c)

(d)

Ans. (a), (c)

Sol.

is also solution of given differential equation atleast.

Option (a), (c) are correct.

39. Let be a vector field given by If C is the curve of intersection of the surfaces x² + y² = 1 and y + z = 2 then which of the following is/are equal to

(a)

(b)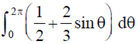

(c)

(d)

Ans. (a), (b)

Sol.

Option (a), (b) are correct.

40. Let V be the set of 2 × 2 matrices with complex entries such that a₁₁ + a₂₂ = 0. Let W be the set of matrices V with a₁₂ + a₂₁ = 0. Then, under usual matrix addition and scalar multiplication which of the following is/are true?

(a) V is a vector space over C

(b) W is a vector space over C

(d) W is a vector space over R

Ans. (a), (c), (d)

Sol.

Option (a), (c), (d) are correct.

41. If the set with real entries then x is equal to _________.

Ans. –1

Sol. For the set to be linearly dependent, there exist

Hence x = –1.

Correct answer is –1.

42. If 5²⁰¹⁵ = n(mod 11) and n ∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} then n is equal to __________.

Ans. 1

Sol. 5²⁰¹⁵ mod 11 – (5⁵)⁴⁰³ mod 11 – (5⁵ mod 11)⁴⁰³ mod 11 = (25 · 25 · 5 mod 11)⁴⁰³ mod 11 = (3 · 3 · 5 mod 11)⁴⁰³ mod 11 = (1⁴⁰³) mod 11 = 1 mod 11 = 1. Hence, n = 1.

Correct answer is 1.

43. If the power series converges for |x| < c and diverges for |x| > c then the value of c correct upto three decimal places is _________.

Ans. 1.648

Sol. By ratio test for convergence

Correct answer is 1.648.

44. The number of distinct normal subgroups of S₃ is _________.

Ans. 1

Sol. S₃ = {(12), (13), (23), (123), (132), (1)}. O(S₃) = 6. Subgroups would have orders 1, 2, 3 or 6.

Subgroups of S₃ are (i) {(1)} (ii) {(12), (1)} (iii) {(13), (1)} (iv) {(23), (1)}, (v) {(1), (123), (132)} and (vi) S₃. Obviously, (i) and (iv) are normal subgroups (ii) is not a normal subgroup as (23) {(12), (1)} = {(132), (23)} up as a {(1), (123), (132)} = {(1), (123), (132)}⋅ a, for all a S₃.

Hence, number of normal subgroups of S₃ is 3.

Correct answer is 1.

45. Let C be the straight line segment from in the xy-plane. Then the value of _________.

Ans. 1

Sol.

Correct answer is 1.

46. Let be defined by f(x, y) = .

If the directional derivative of f at (0, 0) exists along the direction where then the value of cot is _________.

Ans. –1

Sol. By definition

For, this limit to exist

Correct answer is –1.

47. Let be a continuously differentiable function such that f has finitely mainly zeros in (0, 1) and f changes sign at exactly two of these points. Then for any , the maximum number of solutions of f(x) = y in (0, 1) is _________.

Ans. 3

Sol. changes sign at exactly two points, so f has extrema at these two points, say Also is continuous, so f must have a maximum and a minimum at these two points Taking minimum at and maximum at possible graph of y = f(x) would be as shown below. Hence, number of solution of y = f (x) can be maximum 3.

Correct answer is 3.

48. Let be defined by f(x, y, z) = sin x + 2e^y/2 + z². The maximum rate of change of f at correct upto three decimal place is _________.

Ans. 2.345

Sol.

Maximum rate of change off at

Correct answer is 2.345.

49. Let S be the portion of the surface z = bounded by the planes x = 0, x = 2, y = 0 and y = 3. The surface area of S correct upto three decimal place is _________.

Ans. 6.283

Sol.

Correct answer is 6.283.

50. Let be defined by f(x) =

The number of points at which f is continuous is _________.

Ans. 2

Sol. For continuity f(a) =

Correct answer is 2.

51. The coefficient of in the Taylor series expansion of the function f(x) = 3 sin x cos, about the point correct upto three decimal is _________.

Ans. 1.414

Sol.

Taylor expansion of f,

f(x) =

Correct answer is 1.414.

52. Let R be the planar region bounded by the planes x = 0, y = 0 and the curves x² + y² = 4 in the first quadrant. Let C be the boundary of R oriented counter-clockwise. Then the value of _________.

Ans. 8

Sol.

Correct answer is 8.

53. Let P and Q be two real matrices of size 4 × 6 and 5 × 4 respectively. If rank(Q) = 4 and rank (QP) = 2 then rank(P) is equal to ________.

Ans. 2

Sol. Size of QP = 5 × 6. Taking

Clearly, rank (QP) = 2, rank (Q) = 4 and rank (P) = 2.

Since, rank (P) must have a definite numerical value; So that value ample as well. Hence, rank (P) = 2.

Alternatively,

Start with the linear system,

QPx = 0, Px = 0

since rank Q = 4 and Px is a 4 × 1 vector. This implies null space of P and QP are same. Consequently, rank of P and QP are same.

Hence, rank (P) = rank (QP) = 2.

Correct answer is 2.

54. Let l be the length of the portion of the curve x = x(y) between the lines y = 1 and y = 3 where x(y) satisfies

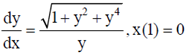
The value of l, correct upto three decimal places is _________.

Ans. 5.098

Sol.

Correct answer is 5.098.

55. If has the power series expansion then a₅, correct upto three decimal places is equal to _______.

Ans. 0.108

Sol.

Correct answer is 0.108.

56. Let be the vector space of 2 × 2 real matrices. Let V be a subspace of defined by

Then, the dimension of V is _________.

Ans. 2

Sol.

Out of a, b, c, d, only two are linearly independent and remaining two are dependents. We can take a, b as independents then c = 3b/2 and d = a + b/2. Hence, dim V = 2.

Correct answer is 2.

57. Suppose G is a cyclic group and are such that order Then the order of the smallest group containing is _________