1. The least positive integer n, such that is the identity matrix of order 2, is

(a) 4

(b) 8

(c) 12

(d) 16

Ans. (b)

Sol.

So n = 8

Matrix A⁸ = identity matrix of order 2.

2. Let S = {T : T is a linear transformation with T(1, 0, 1) = (1, 2, 3) and T(1, 2, 3) = (1, 0, 1). Then S is

(a) a singleton set

(b) a finite set containing more than one element

(c) a countable infinite set

(d) an uncountable set

Ans. (d)

Sol. Here, T(1, 0, 1) = (1, 2, 3), T (1, 2, 3) = (1, 0, 1)

Here we can define the transformation for the third independent element in any ways. For instance, let (0, 0, b) be the third element. This is linearly independent to (1, 0, 1) and (1, 2, 3) for any b , we get a different linear transformation and since is uncountable, So is the S.

3. Let for h 1. Then as n the sequence {s_n} tends to

(a) 0

(b) 1/2

(c) 1

(d)

Ans. (b)

Sol.

4. The workdone by the force in moving a particle over the circular path x² + y² = 1, z = 0 from (1, 0, 0) to (0, 1, 0) is

(a)

(b)

(c)

(d)

Ans. (d)

Sol.

5. The set of all boundary points of in is

(a)

(b) \

(c)

(d)

Ans. (a)

Sol. By the definition of boundary point, the points whose every nbd have the points which belongs to and both are s.t. b boundary point of in .

So, x , and > 0, both rationals and irrationals in each -nbd of x. So, the boundary of in is equal to .

6. Let and for (x, y, z) V. Let denote the outward unit normal vector to the boundary of V and S denote the part of the boundary of V. Then is equal to

(a)

(b)

(c)

(d)

Ans. (a)

Sol. Outward unit normal to boundary of V,

7. The set is

(a) open

(b) closed

(c) both open and closed

(d) neither open nor closed

Ans. (b)

Sol.

The intersection point of y(x) = sin x and are in discrete set. And complement of that set is open. Hence is a closed set.

8. Let where g is a real valued continuous function on . Then is equal to

(a) 0

(b) x³g(x)

(c)

(d)

Ans. (d)

Sol. (By Leibnitz Rule)

9. Let y₁(x) and y₂(x) be linearly independent solutions of the differential equation + Q(x)y = 0 where P(x) and Q(x) are continuous function on internal I. Then y₃(x) = ay₁(x) + by₂(x) and y₄(x) = cy₁(x) + dy₂(x) are linearly independent solutions of the given differential equation if

(a) ad = bc

(b) ac = bd

(c)

(d)

Ans. (c)

Sol. y₃(x) and y₄(x) is linearly independent.

Let a₁ and b₁ s.t. a₁ = b₁ = 0. Then a₁.y₃(x) + b₁y₄(x) = 0

a₁(ay₁(x) + by₂(x)) + b₁(cy₁(x) + dy₂(x)) = 0

a₁ay₁(x) + a₁by₂(x) + b₁cy₁(x) + b₁dy₂(x) = 0

(a₁a + b₁c)y₁(x) + (a₁b + b₁d)y₂(x) = 0 y₁(x) and y₂(x) also linear independent

b₁ = 0 if (bc – ad) 0 bc ad. Similarly, a₁ = 0 if ad bc.

10. The set R = {f | f is a function from to } under the binary operations + and defined as (f + g) (n) = f (n) + g (n) and (f.g) (n) = f (n) g (n) for all forms a ring. Let S₁ = {f R | f (–n) = f (n) all } and S₂ = {f R | f(0) = 0}. Then

(a) S₁ and S₂ are both ideals in R

(c) S₁ is an ideal in R while S₂ is not

(c) S₂ is an ideal in R while S₁ is not

(d) neither S₁ nor S₂ is an ideal in R

Ans. (c)

Sol. S₁ = {f R : f (–n) = f (n) n z} even functions.

Let f S₁ and g R = {f : f is function from Z to R}

f g (– n) = f (– n) • g (– n) = f (n) • g (–n).

Then for g (– n) may or may not be equal to g (n). Hence we can not say that S₁ is ideal.

But for S₂, f S₂, g R

Then f g (0) = f (0) • g (0) = 0 • g (0) = 0

Hence f g S₂ so S₂ is an ideal of R.

11. Let T : be a linear transformation such that T(1, 2, 3) = (1, 2, 3), T(1, 5, 0) = (2, 10, 0) and T(–1, 2, –1) = (–3, 6, –3). The dimension of the vector space spanned by all the eigenvectors of T is

(a) 0

(b) 1

(c) 2

(d) 3

Ans. (d)

Sol. T(1, 2, 3) = (1, 2, 3)

T(1, 5, 0) = (2, 10, 0)

T(–1, 2, –1) = (–3, 6, –3)

So, there are 3 distinct eigen values 1, 2, 3 and correspondingly three L.I. eigen vectors . So dimension of vector space spanned by is 3.

12. Let {a_n} and {b_n} be sequences of real number defined as a₁ = 1 and for n 1, a_n+1 = a_n + (–1)ⁿ 2 ^–n, Then

(a) {a_n} converges to zero and {b_n} is a Cauchy sequence

(b) {a_n} converges to a non-zero number and {b_n} is a cauchy sequence

(c) {a_n} converges to zero and {b_n} is not a convergent sequence

(d) {a_n} converges to a non-zero number and {b_n} is not a convergent sequence

Ans. (b)

Sol. a₂ = 1 + (–1) 2^–1, a₃ = 1 + (–1) 2^–1 + 2^–2, a₄ = 1 + (–1) 2^–1 + 2^–2 – 2^–3,…..

{a_n} is a geometric progression with common ratio

So, {b_n} also converges and converges to 1. So, it is a Cauchy sequence.

13. Let f (–1, 1) be defined as for x 0 and f (0) = 2. If is the Taylor expansion of f for all x in (–1, 1), then is

(a) 0

(b)

(c) 1

(d) 2

Ans. (a)

Sol.

14. Let y₁(x) and y₂(x) be twice differentiable function on a interval I satisfying the differential equation and Then y₁(x) is

(a)

(b)

(c)

(d)

Ans. (c)

Sol. …(1)

…(2)

Solve D × (1) + (2), we get

D(D – 1)y₁ – Dy₂ = De^x

(2D – 6)y₁ + Dy₂ = 0

[D(D – 1) + (2D – 6)]y₁ = e^x [ De^x = e^x]

[D² – D + 2D – 6]y₁ = e^x [D² + D – 6]y₁ = e^x

Auxiliary equation m² + m – 6 = 0 m² + 3m – 6 = 0

m(m + 3) – 2(m + 3) = 0 (m – 2) (m + 3) = 0 m = 2, –3

15. Let G be a finite group and H be normal subgroup of G of roder 2. Then the order of the centre of G is

(a) 0

(b) 1

(c) an even integer 2

(d) an odd integer 3

Ans. (c)

Sol. Since centre of a group is also a subgroup of the group. And order of any subgroup divides order of the group.

And also, H is a normal subgroup of G of order 2. Hence 2|O(G). Also, in centre of G, H is contained and so order of G must be an even integer 2.

16. (a) Let f and g be continuous functions on such that and

Prove that (f (x))² + (g (x))² = 1 for all

(b) Let f : be a function such that is continuous on . Show that the series converges uniformly on [0, 1].

Sol. (a) (using Leibniz's rule)

(using Leibniz's rule)

Let h(x) = (f(x))² + (g(x))²

h'(x) = 2f(x) + 2g(x) g(x)

= 2f(x) g(x) + 2g(x) (–f(x))

= 2f(x) g(x) – 2g(x) f(x)

= 0

h(x) = constant = h(0) = f(f(0))² = 0² + 1² = 1

Hence, (f(x))² + (g(x))² = 1 for all

(b) f : R R be a function s.t. is continuous.

As is continuous so above sum is giving to be a finite value so, it will converge uniformly on (0, 1)

Also, by M_n test.

Here converges is uniform on [0. 1].

17. (a) Find the maxima, minima and saddle points, if any, for function

f (x, y) = (y – x²) (y – 2x²) on

(b) Let P(x) = a₀ + a₁x² + a₂x⁴ + a₃x⁶ +……… + a_nx^2x, where n 1 and

a_k > 0 for k = 0, 1,……n. Show that P(x) = 0 has exactly two real roots.

Sol. (a) f_x (x, y) = –2x(y –2x²) – 4x(y – x²) = –2x(3y – 4x²)

f_y(x, y) = y – 2x² + y – x² = 2y –3x²

f_xx (x, y) = –2(3y – 4x²) + 16x² = –2(3y – 12x²) = –6(y – 4x²)

f_xy (x, y) = –6x

f_yy (x, y) = 2

f_x (x, y) = 0 –2x(3y – 4x²) = 0 x = 0 or 3y – 4x² = 0 ...(1)

f_y (x, y) = 0 2y – 3x² 0 2y = 3x² ...(2)

Solving x = 0 and 2y = 3x² (x, y) (0, 0)

Solving 3y = 4x² and 2y = 3x² (x, y) (0, 0)

So, the only critical point is P(0, 0)

f_xx (0, 0) = f_xy (0, 0) = 0, f_yy (0, 0) = 2

Discriminant of f at

So, the test is inconclusive.

In any neighbourhood 0 < x² + y² < , there are point at which and there are points at which

So, f has neither minimum nor maximum at (0, 0) but it has saddle point at (0, 0).

(b) 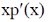= 2a₁x² + 4a₂x⁴ + 6a₃x⁶ + …………+ 2na_nx²ⁿ

p(x) – = a₀ – a₁x² – 3a₂x⁴ – 5a₃x⁶………… –(1 – 2n)a_nx²ⁿ

Let g(x) = p(x) –

g'(x) = –2a₁x – 12a₂x³ – 30a₃x⁵………… –(2n) (1 – 2n) a_nx^2n–1

= –x(2a₁ + 12a₂x² + 30a₃x⁴ + ………… + (2n) (1 – 2n)a_nx^{2n – 2})

> 0 for x < 0 and < 0 for x > 0. So, g(x) has maximum at x = 0

g(0) = p(0) – 0. = a₀ > 0

Hence, g is increasing on having exactly one root in and decreasing on having exactly one root in .

So, p(x) – has exactly two points.

18. (a) Given that y₁(x) = x is a solution of (1+x²)yⁿ – + 2y = 0, x > 0, find a second linearly independent solution .

(b) Solve x²yⁿ + – y = 4x log x, x > 0.

Sol.

…(1)

u = x is the independent solution let the complete solution y = uγ

so put and in equation (1)

so second linearly independent solution is y = (x² – 1)

This differential equation is homogeneous

complement function y = c₁e^z + c₂e^–z,

Complete solution is y = CF + PI, y = c₁e^z + e^z (z² – z).

19. (a) Let be a differential function on [0, 1] satisfying for all with (0) = 0. Show that e^3x – 1. (6)

(b) If y₁(x) = x(1 – 2x), y₂(x) = 2x(1 – x) and y₃(x) = x(e^x – 2x) are three solutions of a non-homogeneous linear differential equation + Q(x)y = R(x), where P(x), Q(x) and R(x) are continuous function on [a, b] with a>0, then find its general solution.

Sol.

(b) General solution of a non-homogeneous linear differential equation.

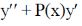+ Q(x)y = R(x). Then solution y = CF + PI complementary function.

CF = c₁f₁(x) + c₂f₂(x)

y = c₁f₁(x) + c₂f₂(x) + PI

The solution of differential equation are

y₁(x) = x – 2x², y₂(x) = 2x – 2x², y₃ (x) = xe^x – 2x²

P.I. is common in every solution. From y₁(x), y₂(x) it can be conclude that

PI = –2x², then f₁(x) = x, f₂ (x) = xe^x

So, general solution of differential equation is

y = c₁x + c₂xe^x – 2x².

20. (a) Evaluate

(b) Find the surface area of the portion of the cone z² = x² + y² that is inside the cylinder z² = 2y.

Sol.

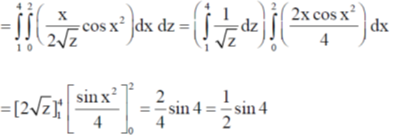
(b) Cone: z² = x² + y²

Cylinder: z² = 2y

Solving the two equations:

x² + y² = 2y

x² + (y – 1)² = 1

Projection of the intersection of the two surface on the xy plane would be the circle x² + (y – 1)² = 1

The surfaces are symmetrical about the xy-plane so, the similar surfaces would be cut below the xy-plane, as shown in the figure.

So, the required surface area,

21. (a) Using Green's theorem to evaluate the integral where C is the closed curve given by y = 0, y = x and y² = 2 – x in the first quadrant, oriented counter clockwise.

(b) Let f : be a continuous function. Use change of variables to prove that

Sol.

(b)

Boundaries of D : x + y = 1, x + y = –1, x – y = –1, x – y = 1

Let u = x + y and = x – y

22. Using Gauss's divergence theorem, evaluate the integral where S is the surface of the solid bounded by the sphere x² + y² + z² = 10 and the paraboloid x² + y² = z – 2, and is the outward unit normal vector to S.

Sol.

Surface bounding the volume are

x² + y² + z² = 10 and x² + y² = z – 2

(a) Part-I: Show V is vector space over a field .

To show V is vector space following condition must hold

(1) (V, +) is abelian group

(2)

(3) (i)

(ii)

(iii)

(iv)

(1) (V, +) is abelian group

(i) Closure property:

Let M₁, M₂ M₁ and M₂ are skew Hermitian matrix

Consider M₁ + (M₂ + M₃) =

It follow associative law.

(iii) Existence of Identity: For matrix M identity element is zero vector w.r.t. addition.

(iv) Existence of Inverse: For every matrix M V we find –M s.t. M + (–M) = e where –M V

(v) Commutative: Let

(V, +) is abelian group.

(2)

then consider

aM₁ is skew Hermitian

(3) (i)

Let a(M₁ + M₂) = aM₁ + aM₂

(ii)

(iii)

(iv)

V is vector space over .

Part-II: Show V is vector space over

Consider to show If cM

Consider

V is not a vector space over complex number.

(b) V = {p(x) | p(x) is a polynomial of degree n with real coefficient}.

Let P₁(x), P₂(x) V T[aP₁(x) + bP₂(x)] = {aP₁(1) +bP₂(1), aP₁(2),…, aP₁(m) + bP₂(m)}

= (aP₁(1), aP₁(2)….aP₁(m)) + (bP₂(1),bP₂(2),……,bP₂(m)

= a(P₁(1)),……P₁(m)) + b(P₂(1)……P₂(m)) = aT(P₁(x)) + bT(P₂(x))

T is a linear transformation.

For nullity of T

Let T(P₁(x)) = (0, 0, 0,….0) (P(1), (2),……P(m) = (0, 0,…0)

P(1) = P(2) = ….. = P(m) = 0

If degree of P(x) = n m, then polynomial will be identically zero.

If degree of P(x) = n > m

then P(x) = f(x)(x – 1)(x – 2)…..(x – m) written in this form s.t.

P(1) = P(2).… = P(m) = 0

P(x) = f(x)(x – 1)(x –2)…..(x – m) where f(1) 0, f(2) 0…..f(m) 0]

Nullity = dim of null space,

Here Null space N(t) = {P(x)|

P(x) = f(x) (x–1) …. (x–m)} Nullity = n – m

23. (a) A square matrix M of order n with complex entries is called skew Hermitian if where 0 is the zero matrix of order n. Determine whether V = {M | M is a 2 × 2 skew Hermitian matrix} is a vector space over

(i) the field ¡ and

(ii) the field with usual operation of addition and scalar multiplication for matrices

(b) Let V = {P(x) | P(x) is a polynomial of degree n with real coefficients and T : V be defined as T(P(x)) = (P(1), P(2)……P(m)). Show that T is linear and determine the nullity of T.

Sol.

24. Let G be the set of all 3 × 3 real matrices M such MM^T = M^T M = I₃ and let H = {M G | det M = 1}, where I₃ is the identity matrix of order 3. Then shown that

(i) G is a group under matrix multiplication,

(ii) H is a normal subgroup of G,

(iii) {–1, 1} given by (M) = det M is onto,

(iv) G/H is abelian.

Sol. (i) To show that G be group under matrix multiplication when G be the set of all 3 × 3 real matrix M s.t. MM^T = M^T M = I₃

Since all the matrixes of order 3 × 3 with real entries say P make a group under matrix multiplication so need to prove that G be group enough to prove that it is subgroup of P. So let M, N G to show that M N^–1 G

M G MM^T = M^TM = I

N G NN^T = M^TM = I

(M N^–1) (M N^–1) = M N^–1. (N^–1 T · M^T)

M (N^–1 N^–1T) M^T = M[(N^–1) (N^T)^–1]·M^T

M (N^T N)^–1 M^T = M I·M^T = MM^T = I

M N^–1 G. Thus G is group

By the property of transposition of matrix.

(ii) To prove that H is normal subgroup of G where H = {M G: det M = 1}.

A H and B M, then

|B^–1 AB| = |B^–1||A|·|B| = |A·|·|B^–1|·|B| = 1

Thus B^–1 AB H.

(iii) (M) = det M is on to

As M^T = M^–1 [By the property MM^T = M^TM = I]

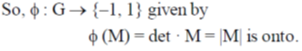
HA and HB are elements of

HA HB = H H A B [ H is normal subgroup of 4]

= H A B = H B A = H B H A.

Thus HA · HB = HB · HA

Hence is abelian.

25. (a) Suppose that (R, +, .) is a ring having the property a·b = c·a b = c, when a 0. Then prove that (R, +,.) is a commutative ring.

(b) Let R be a commutative ring with identity. For a₁, a₂, ……, a_n R, the ideal generated by {a₁, a₂, …… a_n} is given by

Let be the set of all polynomials with integer coefficients. Consider the ideal I = {f Z[x]| f (0) is an even integer}. Prove that and that it is a maximal ideal.

Sol. (a) Given (R, +, ·) is a ring having the property that a · b = c · a b = c when

Also, we have if a · b = a · c and a 0

By cancellation law,

So we have,

ab = ac –– (i) When a 0

ab = ca –– (ii)

By (i) and (ii), we have

a · c = c · a

and so, (R, +.) is a commutative ring.

(b) Z[x] be the polynomial ring with integer coefficients

I = {f Z [x]: f(0) is an even integer}

Since, means.

2· f(x) + x·g(x) = h(x)

 h(0) = 2· f(0)

h(0) is an even integer.

Since f (0) can be either even or odd. And in both cases 2·f (0) will be even.

Hence, I = is an ideal.

Support J contains property I. Thus a poly r(x) with odd constant term say a. Thus, a – 2 = odd J. And so J = Z[x].

Hence I is maximal ideal in Z[x].

26. For a given positive integer n > 1, show that there exist subspaces X₁,X₂,……X_n of for some integer m>n and a linear transformation T : such that

Also, find the rank of T.

Sol. Part-I: Show X_K is subspace of R^m. X_K = (x₁, x₂……x_k, 0, 0,….0). Let x, y X_k and a, b F, consider ax + by = a(x₁, x₂,…., x_k, 0, 0,….0) + b(y₁, y₂,…., y_k, 0, 0,….0)

= (ax₁, ax₂,….ax_k, 0, 0,….0) + (by₁, by₂…by_k, 0, 0,….0)

= (ax₁ + by₁, ax₂ + by₂….ax_k + by_k, 0,…0) X_K

X_K is subspace of R^m.

Part-II: Show T is linear transformation consider x, y Rⁿ

T(ax + by) = T(a(x₁….x_k, 0,….0) + b(y₁….y_k, 0,….0) = T((ax₁ + by₁…. ax_k + by_k, 0,….0)

= (ax₁ + by₁…., ax_k–1 + by_k–1, 0,…0) = a(x₁….x_k–1, 0,…0) + b(y₁….y_k–1, 0,….0)

= aT(x) + bT(y) (T(X_K) = X_K–1)

T is a linear transformation

Part-III: Rank of T

Let T(X_K) = (0, 0….0) (x₁, x₂….x_k–1, 0, 0,….0) = (0, 0,….0)

x₁ = x₂ = x_k–1 = 0 x_k null space

i.e. N(T) = {0, 0…., x_k, 0,…0)} dim N(T) = 1

dim R(T) + dim N(T) = dim R dim of range of t = m – 1

27. Let F : be a continuously differentiable function and let be defined for xy 0.

(a) Prove that

(b) Further, if f is homogeneous of degree then verify that

Sol.

…(1)

Since, any homogeneous function f of degree can be written as for some function g, (1) holds true for all such functions f.

28. Determine the interval of the power series and show that its sum is at point x in its interval of convergence.

Sol.

Given that u_n = n·(2n – 1)

So, R = 1

again, we will start by simple expression.

differentiate both sides.

again differentiate both sides.

29. (a) Let f : be defined as and f (x,y) = 0 for x = 0.

Compute at all points in and shown that it is continuous at the origin.

(b) Let f : (0, 1) be a uniformly continuous function. If {x_n} is Cauchy sequence in (0, 1), then prove that {f(x_n)} is Cauchy sequence in 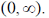Hence deduce that for any two Cauchy sequences {x_n} and {y_n} in (0, 1), {|f(x_n) – f(y_n)|} is a Cauchy sequence is

Sol.

= 0 + 0 = 0

So, f_x is continuous at (0, 0).

(b) {x_n} is a Cauchy sequence For any > 0, there exists n₀ such that |x_m – x_n| < for all m,n ≤ n₀. m, n , x_m, x_n (0, 1) ...(1)

f is uniformly continuous on (0, 1) There exists a for any > 0, such that

Choosing x, y {x_n}, and saying x = x_n and y = x_m, we have for any > 0, there a , such that

So, for any Cauchy sequence {x_n} and {y_n}, {f(x_n)}, {f(y_n)} are Cauchy sequences. Substraction of two cauchy sequences is alos a Cauchy sequence. And modulus of a Cauchy sequence is a Cauchy sequence. Hence, {|f(x_n) – f(y_n)|} is a Cauchy sequence.