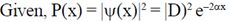1.    Consider the linear differential equation 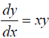. If y = 2 at x = 0 then the value of y at x = 2 is given by

    (a)    e^–2

    (b)    2e^–2

    (c)    e²

    (d)    2e²

Ans.    (d)

Sol.    

    Putting x = 2, we get    

    

2.    Which of the following magnetic vector potentials gives rise to a uniform magnetic field ?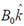

    (a)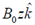

    (b)

    (c)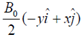

    (d)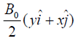

Ans.    (c)

Sol.    

    We have, 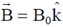, only option (c) satisfy the above condhion.

3.    The molecule ¹⁷O₂ is

    (a)    Raman active but not NMR (nuclear magnetic resonance) active

    (b)    Infrared active and Raman active but not NMR active

    (c)    Raman active and NMR active

    (d)    Only NMR active

Ans.    (c)

Sol.    For Raman active, there must be change in polarizability. Since ¹⁷O₂ is homo diatomic molecule therefore, it will have change in polarizability, thus it will be Raman active. Netdipole moment in ^l7O₂ is zero, so IR inactive ^l7O₂ has nuclear spin I = 5/2, therefore, it is NM R active.

4.    There are four electrons in the 3d shell of an isolated atom. The total magnetic moment of the atom in units of Bohr magneton is ______________.

Ans.    0

Sol.    For the 4, 3-d-electrons;

    

    

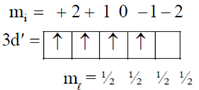
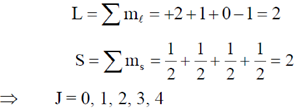
    Since shell is less than half filled, total angular momentum for ground state term J = 0.

    The resultant magnetic momentum is given by

    µ = gµ_J = 0 [J = 0]

5.    Which of the following transitions is NOT allowed in the case of an atom, according to the electric dipole radiation selection rule?

    (a)    2s – 1s

    (b)    2p – 1s

    (c)    2p – 2s

    (d)    3d – 2p

Ans.    (a)

Sol.    For electric dipole radiation, selection rule is 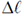= ± 1.

    Here, in option for transition 2s 1s, we have , which is forbidden.

    Thus, 2s 1s is not allowed.

6.    In the SU(3) quark model, the triplet of meson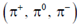s has

    (a)    Isospin = 0, Strangeness = 0

    (b)    Isospin = 1, Strangeness = 0

    (c)    Isospin = 1/2, Strangeness = +1

    (d)    Isospin = 1/2, Strangeness = –1

Ans.    (b)

Sol.    For triplet of mesons, 21 + 1 = 3 1 = 1

    Mesons are not strange particles. Therefore, S = 0

7.    The magnitude of the magnetic dipole moment associated with a square shaped loop carrying a steady current I is m. If this loop is changed to a circular shape with the same current I passing through it, the magnetic dipole moment becomes 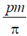. The value of p is _____________

Ans.    4

Sol.    We know magnetic moment,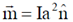

    where a is the side of the square and is unit vector normal to the surface

    If the square is converted into circle and radius of the circle is r, then

    

    So, magnetic moment,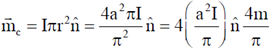

    So, P = 4

8.    The total power emitted by a spherical black body of radius R at a temperature T is P₁. Let P₂ be the total power emitted by another spherical black body of radius R/2 kept at temperature 2T. The ratio, P₁/P₂ is _________. (Give your answer upto two decimal places).

Ans.    0.25

Sol.    According to Stefen-Boltzman law, power emitted from the black body is given

    P 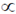AT⁴    where, A = reading area, T = temperature of black body

    

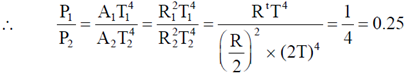
9.    The entropy S of a system of N spins, which may align either in the upward or in the downward direction, is given by S = –k_BN [p ln p + (1 – p) ln (1 – p)]. Here k_B is the Boltzmann constant. The probability of alignment in the upward direction is p. The value of p, at which the entropy is maximum, is _____. (Give your answer upto one decimal place).

Ans.    0.5

Sol.    Given: S = –k_BN[p ln p + (1 – p) ln (1 – p)]

    For maxima and minima,

    

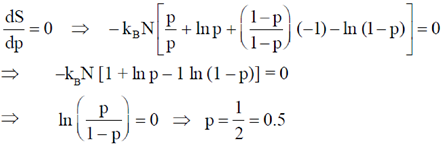
10.    For a system at constant temperature and volume, which of the following statements is correct at equilibrium?

    (a)    The Helmholtz free energy attains a local minimum

    (b)    The Helmholtz free energy attains a local maximum

    (c)    The Gibbs free energy attains a local minimum

    (d)    The Gibbs free energy attains a local maximum

Ans.    (a)

Sol.    The Helmholtz free energy (F) is defined as

    F = U – TS

    dF = dU – TdS – SdT

    = TdS – PdV – TdS – SdT    [ dU=TdS – PdV]

    = – PdV – SdT

    At constant temperature and volume,

        dF = 0

    So F is either maximum or minimum for a system at constant volume and temperature. Moreover the second law of thermodynamics sets a limit that in any process at constant volume and temperature, the Helmholtz free energy decreases.

    i.e.,    dF < 0.

    where equality holds for reversible and inequality for irreversible processes.

    So, Helmholtz free energy decreases and hence minimum at equilibrium.

11.    N atoms of an ideal gas are enclosed in a container of volume V. The volume of the container is changed to 4V, while keeping the total energy constant. The change in the entropy of the gas, in units of Nk_B ln 2, is _______, where k_B is the Boltzmann constant.

Ans.    2

Sol.    From first law of thermodynamics,

    dQ = dU + PdV

    It is given that the total energy is constant.

    

    

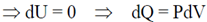
12.    Which of the following is an analytic function of z everywhere in the complex plane?

    (a)    z²

    (b)    (z^*)²

    (c)    |z|²

    (d)

Ans.    (a)

Sol.    Let z = x + iy

    f(z) = z² = (x² – y²) + 2xyi = u + iv

    Here, u = x² – y², v = 2xy

    

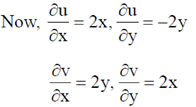
    Therefore, Cauchy Reamanh equation is satisfied i.e.

    

13.    In a Young's double slit experiment using light, the apparatus has two slits of unequal widths. When only slit-1 is open, the maximum observed intensity on the screen is 4I₀. When only slit-2 is open, the maximum observed intensity is I₀. When both the slits are open, an interference pattern appears on the screen. The ratio of the intensity of the principal maximum to that of the nearest minimum is _____________.

Ans.    9:1

Sol.    When slit–1 open    when slit –2 open

    a² = 4I₀            b² = I₀

    

    So, when both are open

    

14.    Consider a metal which obeys the Sommerfeld model exactly. If E_F is the Fermi energy of the metal at T = 0K and R_H is its Hall coefficient, which of the following statements is correct?

    (a)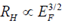

    (b)

    (c)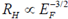

    (d) R_H is independent of E_F

Ans.    (c)

Sol.    Fermi energy can be given by 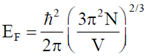            ...(i)

    where, electron concentration per unit volume.

    

    and Hall coefficient can be given by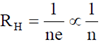

    

15.    A one-dimensional linear chain of atoms contains two types of atoms of masses m₁ and m₂ (where m₂> m₁), arranged alternately. The distance between successive atoms is the same. Assume that the harmonic approximation is valid. At the first Brillouin zone boundary, which of the following statements is correct?

    (a)    The atoms of mass m₂ are at rest in the optical mode, while they vibrate in the acoustical mode.

    (b)    The atoms of mass m₁ are at rest in the optical mode, while they vibrate in the acoustical mode.

    (c)    Both types of atoms vibrate with equal amplitudes in the optical as well as in the acoustical modes.

    (d)    Both types of atoms vibrate, but with unequal, non-zero amplitudes in the optical as well as in the acoustical modes.

Ans.    (a)

Sol.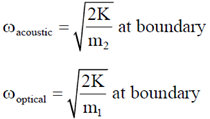    

16.    Which of the following operators is Hermitian?

    (a)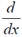

    (b)

    (c)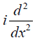

    (d)

Ans.    (b)

Sol.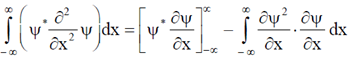    

    

17.    The kinetic energy of a particle of rest mass m₀ is equal to its rest mass energy. Its momentum in units of m₀c, where c is the speed of light in vacuum, is _________. (Give your answer upto two decimal places)

Ans.    1.73

Sol.    Given k = m₀c²    here, k = kinetic energy

    we know that;

    

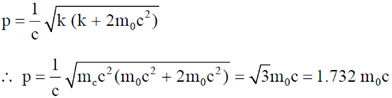
18.    The number density of electrons in the conduction band of a semiconductor at a given temperature is 2×10¹⁹ m^–3. Upon lightly doping this semiconductor with donor impurities, the number density of conduction electrons at the same temperature becomes 4×10²⁰ m^–3. The ratio of majority to minority charge carrier concentration is _______________.

Ans.    400

Sol.    In intrinsic semiconductor, n_i = 2 × 10¹⁹ m^–3

    In doped semiconductor, n = 4 × 10²⁰ m^–3

    By doping with donor impurities, the majority carriers will be electrons (n) and minority carriers will be holes (p).

    From equation = np                                ... (i)

    

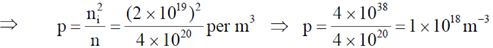
    Therefore, ratio of majority to minority charge carriers

    

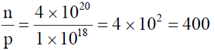
19.    Two blocks are connected by a spring of spring constant k. One block has mass m and the other block has mass 2m. If the ratio k/m = 4s^–2, the angular frequency of vibration 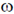of the two block spring system in s^–1 is ___________. (Give your answer upto two decimal places).

Ans.    2.45

Sol.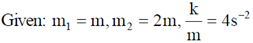    

    Angular frequency for system shown in figure is given as

    

    

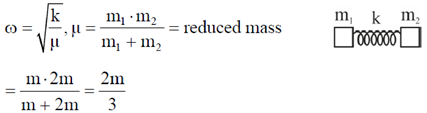
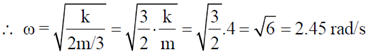
20.    A particle moving under the influence of a central force 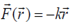(where is the position vector of the particle and k is a positive constant) has non-zero angular momentum. Which of the following curves is a possible orbit for this particle?

    (a)    A straight line segment passing through the origin

    (b)    An ellipse with its center at the origin

    (c)    An ellipse with one of the foci at the origin

    (d)    A parabola with its vertex at the origin

Ans.    (b)

Sol.    Given, , and angular momentum is non zero.

    Particle is moving under two perpendicular restoring forces therefore its dynamics can be resolved into two perpendicular simple harmonic motions. We know that superposition of two perpendicular simple harmonic motions leads to three types of path; Straight line through origin, circle about origin, ellipse about origin. Since angular momentum is non zero path cannot he straight tine through origin.

21.    Consider the reaction . The particle X is

    (a)

    (b) v_e

    (c) n

    (d)

Ans.    (b)

Sol.    Here, in this reaction, we have electron on left hand side, which belong to Lepton family. For the conservation of Lepton number in the above equation, we need to add a I epton member on the right hand side also i.e. either an electron, or electron-neutrino.

    Since, we have electron at left side, we need to add electron neutrino on right side.

22.    The scattering of particles by a potential can be analyzed by Born approximation. In particular, if the scattered wave is replaced by an appropriate plane wave, the corresponding Born approximation is known as the first Born approximation. Such an approximation is valid for

    (a)    large incident energies and weak scattering potentials

    (b)    large incident energies and strong scattering potentials

    (c)    small incident energies and weak scattering potentials

    (d)    small incident energies and strong scattering potentials

Ans.    (a)

Sol.    First Born approximation is .valid if the energy of the incident particle is large and scattering potential is weak.

23.    Consider an elastic scattering of particles in l = 0 states. If the corresponding phase shift is 90º and the magnitude of the incident wave vector is equal to fm^–1 then the total scattering cross section in units of fm² is ___________.

Ans.    2

Sol.    According to parial wave analysis the total scattering cross-section is given by

    

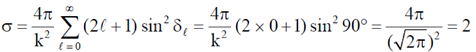
24.    A hydrogen atom is in its ground state. In the presence of a uniform electric field the leading order change in its energy is proportional to (E₀)ⁿ. The value of the exponent n is ___________

Ans.    2

Sol.    In case of hydrogen atom, a uniform electric field is applied. So, this electric field will be treated as a perturbation.

    V_p = – qE₀z = + eE₀r cos

    First order correction to the energy, in the ground state

    

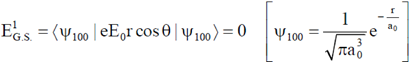
    ln presence of electric field, there is no correction to the first order, Second order correction to the energy in the ground state

    

    This is also well known result in every literature that presence of electric field lifts the degeneracy of energy levels in second order correction which comes out to be proportional to

    Hence, the value of exponent n is (2)

25.    A solid material is found to have a temperature independent magnetic susceptibility, = C. Which of the following statements is correct?

    (a)    If C is positive, the material is a diamagnet

    (b)    If C is positive, the material is a ferromagnet

    (c)    If C is negative, the material could be a type I superconductor

    (d)    If C is positive, the material could be a type I superconductor

Ans.    (b)

Sol.    Susceptibility is defined as 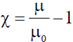, where µ and µ₀ are permeability of medium and vacuum respectively.

    (i) For Diamagnet; µ < µ₀, thus < 0 i.e. is negative

    (ii) For Ferromagnet, µ >> µ₀, thus >> 0 i.e. is positive

    (iii) For superconductor, µ = 0, thus = –1

26.    An infinite, conducting slab kept in a horizontal plane carries a uniform charge density . Another infinite slab of thickness t, made of a linear dielectric material of dielectric constant k, is kept above the conducting slab. The bound charge density on the upper surface of the dielectric slab is

    (a)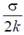

    (b)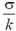

    (c)

    (d)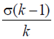

Ans.    (d)

Sol.    The electric field at the upper surface will be

    So, polarization,

    So, surface bound charge,

27.    The number of spectroscopic terms resulting from the L.S. coupling of a 3p electron and a 3d electron is __________ .

Ans.    12

Sol.    For 3p 3d electron, we have

    

    The possible values of S and L are:

    S – |s₁ – s₂|, |s₁ – s₂| + 1, – – – – – , (s₁ + s₂)

    = 0,1: multiplicity (2s + 1) = 1 , 3

    

    =1, 2, 3 (P, D, F states)

    To take into account spin–orbit interaction, let us combine L and Sto form J. Now

    For singlet terms, we have

    

    For triplet terms, we have

    

    Thus a single degenerate level of configuration 3P 3d is splitted into 12 levels.

28.    Which of the following statements is NOT correct?

    (a)    A deuteron can be disintegrated by irradiating it with gamma rays of energy 4 MeV.

    (b)    A deuteron has no excited states

    (c)    A deuteron has no electric quadrupole moment

    (d)    The ¹S₀ state of deuteron cannot be formed

Ans.    (c)

Sol.    Deuteron has binding energy 2.23 MeV. So, can be disintegrated by 4 MeV gamma rays. Deuteron has no excited states. Deuteron ground state is triplet so it cannot have ¹S₀ state. Its quadrupole moment is positive i.e. prolate.

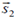29.    If and are the spin operators of the two electrons of a He atom, the value of for the ground state is

    (a)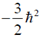

    (b)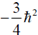

    (c) 0

    (d)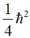

Ans.    (b)

Sol.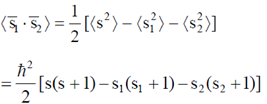    

    

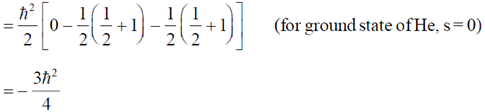
30.    A two-dimensional square rigid box of side L contains six non-interacting electrons at T = 0K. The mass of the electron is m. The ground state energy of the system of electrons, in units of 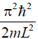is _______

Ans.    24

Sol.    Since, electron is Fermi particle. So, we can place two electron is in each state

    

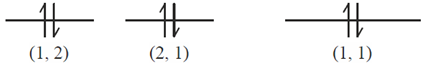
    So, the n^th state energy 2-D potential box is givne by

    Therefore, the ground state energy of the system is

    

31.    An alpha particle is accelerated in a cyclotron. It leaves the cyclotron with a kinetic energy of 16 MeV. The potential difference between the D electrodes is 50 kilovolts. The number of revolutions the alpha particle makes in its spiral path before it leaves the cyclotron is _______

Ans.    80

Sol.    Maximum kinetic energy, K.E_max = 2NqV

    where N is number of revolutions

    V = 50 × 10³ V

    q = 2e^– = 2 × l.6 × 10^–19 C of -particle

    

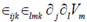32.    Let V_i be the i^th component of a vector field , which has zero divergence. If the expression for is equal to

    (a)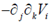

    (b)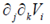

    (c)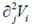

    (d)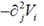

Ans.    (d)

Sol.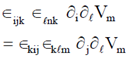    

    

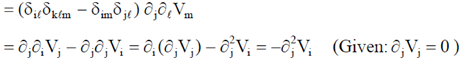
33.    The direction of 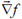for a scalar field 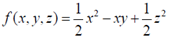at the point P(1, 1, 2) is

    (a)

    (b)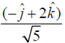

    (c)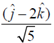

    (d)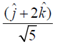

Ans.    (b)

Sol.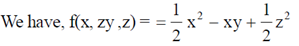    

    

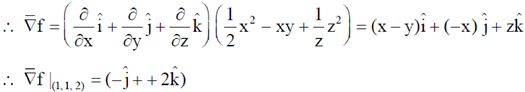
    Therefore, direction of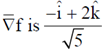

34.    and are the Pauli matrices. The expression is equal to

    (a)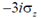

    (b)

    (c)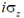

    (d)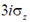

Ans.    (c)

Sol.    

35.    A particle of mass m = 0.1 kg is initially at rest at origin. It starts moving with a uniform acceleration ms^–2 at t = 0. The action S of the particle, in units of J-s, at t = 2s is _________. (Give your answer upto two decimal places).

Ans.    26.67

Sol.    

    

    

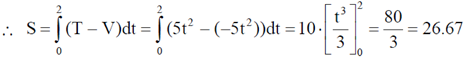
    S = 26.67 J-s

36.    A periodic function f(x) of period 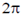is defined in the interval 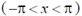as:

    

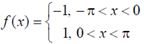
    The appropriate Fourier series expansion for f(x) is

    (a)

    (b)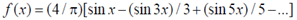

    (c)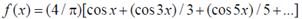

    (d)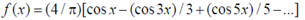

Ans.    (a)

Sol.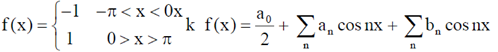    

    Given f(x) is an odd function:

    Therefore, a₀ = 0, a_n = 0

    

    

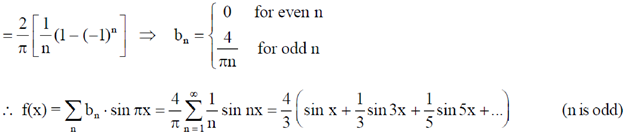
37.    Atoms, which can be assumed to be hard spheres of radius R, are arranged in an fcc lattice with lattice constant a, such that each atom touches its nearest neighbours. Take the center of one of the atoms as the origin. Another atom of radius r (assumed to be hard sphere) is to be accommodated at a position (0, a/2, 0) without distorting the lattice. The maximum value of r/R is ____________. (Give your answer upto two decimal places).

Ans.    0.41

Sol.    Along the 7–axis there are three atoms [two at corners and one at 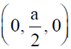. lf a is the lattice parameters.

    Then a = 2R + 2r                                    ...(i)

    Diagonal of each face will have 4 atoms (two at corners and one at center).

    

    Now putting value of R from equation (ii) to equation (i), we get

    

    

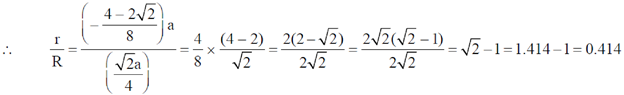
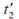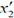38.    In an inertial frame of reference S, an observer finds two events occurring at the same time at co-ordinates x₁ = 0 and x₂ = d. A different inertial frame S' moves with velocity v with respect to S along the positive x-axis. An observer in S' also notices these two events and finds them to occur at times and and at positions and , respectively. If and 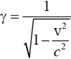, which of the following statements is true?

    (a)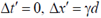

    (b)

    (c)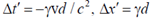

    (d)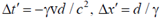

Ans.    (c)

Sol.    

    From Lorentz transformatbn

    

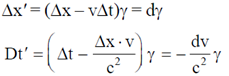
39.    The energy vs. wave vector (E – k) relationship near the bottom of a band for a solid can be approximated as E = A(ka)² + B(ka)⁴, where the lattice constant a = 2.1Å. The values of A and B are 6.3 × 10^–19J and 3.2 × 10^–20J, respectively. At the bottom of the conduction band, the ratio of the effective mass of the electron to the mass of free electron is ________. (Give your answer upto two decimal places)

    (Take 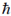= 1.05 × 10^–34J-s, mass of free electron = 9.1 × 10^–31kg)

Ans.    0.22

Sol.    The ratio of effective mass to the free electron mass

    

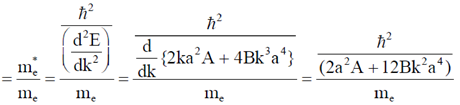
     {at the bottom of conduction band k = 0}

    

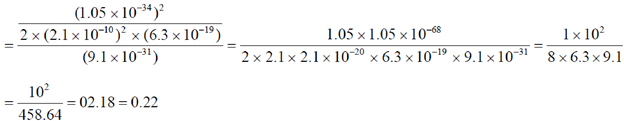
40.    The electric field component of a plane electromagnetic wave travelling in vacuum is given by 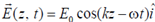. The Poynting vector for the wave is

    (a)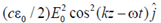

    (b)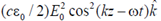

    (c)

    (d)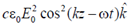

Ans.    (d)

Sol.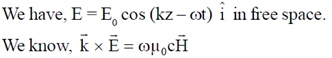    

    

    

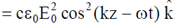
41.    Consider a system having three energy levels with energies 0, 2 and 3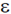, with respective degeneracies of 2, 2 and 3. Four bosons of spin zero have to be accommodated in these levels such that the total energy of the system is 10. The number of ways in which it can be done is ___________.

Ans.    18

Sol.    Let n₁, n₂ and n₃ be the number of particles with energy, 0.22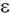 and 3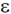. respectively. Then

    According to given,

        n₁ + n₂ + n₃ = 4                                ...(i)

    and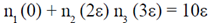    

    or    2n₂ + 3n₂ + 10                                 ...(ii)

    Using equation (ii),

    Since n₁, n₂ and n₃, all are integers, only possible values of n₂ and n₃ are 2 and 2 respectively. Now from equation (i), n₁ = 0.

    So possible values of n₁ = 0, n₂ = 2 and n₃ = 2

    Also, given that g₁ = 2, g₂ = 2 and g₃ = 3.

    The number of microstates for bosons is

    

42.    The Lagrangian of a system is given by

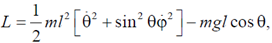     where m, l and g are constants.

    Which of the following is conserved?

    (a)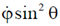

    (b)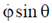

    (c)

    (d)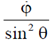

Ans.    (a)

Sol.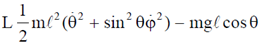    

    

    

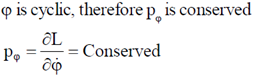
43.    Protons and -particles of equal initial momenta are scattered off a gold foil in a Rutherford scattering experiment. The scattering cross sections for proton on gold and -particle on gold are 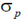and respectively. The ratio 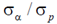is ___________.

Ans.    4

Sol.    Rutherford scattering cross-section

    

44.    For the digital circuit given below, the output X is

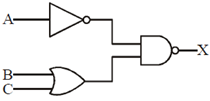
    (a)

    (b)

    (c)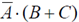

    (d)

Ans.    (b)

Sol.    To find output X

    

    

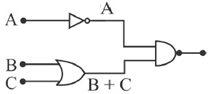
    (By applying De-Morgan's theorem)

    

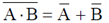
45.    The Fermi energies of two metals X and Y are 5eV and 7eV and their Debye temperatures are 170 K and 340 K, respectively. The molar specific heats of these metals at constant volume at low temperatures can be written as 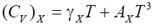and 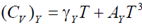where and A are constants. Assuming that the thermal effective mass of the electrons in the two metals are same, which of the following is correct?

    (a)

    (b)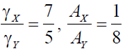

    (c)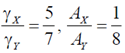

    (d)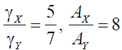

Ans.    (a)

Sol.    The molar specific heat can be given by

    

    

    For X and Y:

    

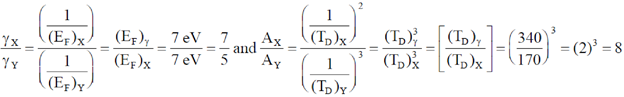
46.    A two-level system has energies zero and E. The level with zero energy is non-degenerate, while the level with energy E is triply degenerate. The mean energy of a classical particle in this system at a temperature T is

    (a)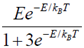

    (b)

    (c)

    (d)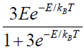

Ans.    (d)

Sol.    The mean energy is

    

47.    A particle of rest mass M is moving along the positive x-direction. It decays into two photons and 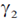as shown in the figure. The energy of 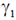is 1GeV and the energy of 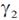is 0.82 GeV. The value of M (in units of GeV/c²) is _____________. (Give your answer upto two decimal places)

Ans.    1.44

Sol.    Apply conservation of momentum in x-direction to get

    

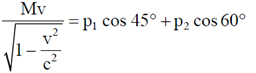
    We have energy momentum relation 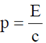for photon

    

    Apply conservation of energy; given E₁ = 1 GeV, E₂ = 0.82 GeV

    

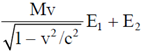
    Divide (i) by (ii) to get

    

    v = 0.614 c

    From equation (ii) we get

    

48.    If x and p are the x components of the position and the momentum operators of a particle respectively, the commutator [x², p²] is

    (a)

    (b)

    (c)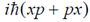

    (d)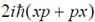

Ans.    (d)

Sol.    

49.    The x-y plane is the boundary between free space and a magnetic material with relative permeability µ_r. The magnetic field in the free space is . The magnetic field in the magnetic material is

    (a)

    (b)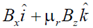

    (c)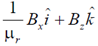

    (d)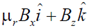

Ans.    (d)

Sol.    According to boundary condition

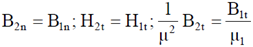     (since, surface current density at the interface is zero)

    We have,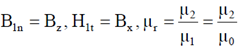

    B_2n = B_z, B_2t = µ_rB_x

    So, magnetic field in the magnetic material will be

    

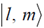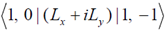50.    Let be the simultaneous eigenstates of L² and L_z. Here is the angular momentum operator with Cartesian components (L_x, L_y, L_z), l is the angular momentum quantum number and m is the azimuthal quantum number. The value of is

    (a) 0

    (b)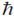

    (c)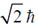

    (d)

Ans.    (c)

Sol.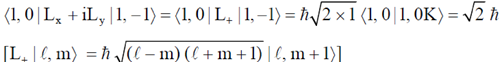    

51.    For the parity operator P, which of the following statements is not true?

    (a)    P^† = P

    (b)    P² = –P

    (c)    P² = I

    (d)    P^† = P^–1

Ans.    (b)

Sol.    We know that, parity operator is hermitian i.e. P^† + P

    Parity operator is also unitary operator i.e. P^† + P^–1

    

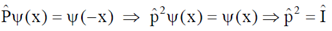
52.    For the transistor shown in the figure, assume V_BE = 0.7V and 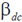= 100. If V_in = 5V, V_out (in Volts) is _________. (Give your answer upto one decimal place).

Ans.    5.7

Sol.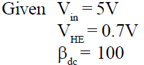    

    

53.    The state of a system is given by

    

    where and form an orthonormal set. The probability of finding the system in the state 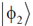is __________. (Give your answer upto two decimal places)

Ans.    0.29

Sol.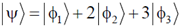    

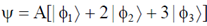    , where A is a normalization constant

    Using the normalization condition,

    

    The probability of finding the system in the state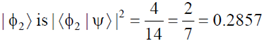

54.    According to the nuclear shell model, the respective ground state spin-parity values of 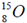and nuclei are

    (a)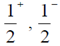

    (b)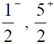

    (c)

    (d)

Ans.    (b)

Sol.    

    N = 15 – 8 = 7

    (¹s_1/2)² (¹p_3/2)⁴ (¹p_1/2)¹

    

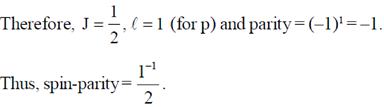
    For , Z = 8 (even)

    N = 17 – 8 = 9

    (¹s_1/2)² (¹p_3/2)⁴ (¹p_1/2)¹ (¹d_5/2)¹

    

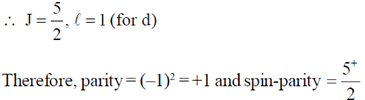
55.    A particle of mass m and energy E, moving in the positive x direction, is incident on a step potential at x = 0 as indicated in the figure. The height of the potential is V₀, where V₀ > E. At x = x₀ where x₀ > 0 the probability of finding the electron is 1/e times the probability of finding it at x = 0. If 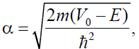the value of x₀ is

    (a)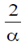

    (b)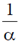

    (c)

    (d)

Ans.    (c)

Sol.    Since, E < V₀, so according to principle of quantum tunneling there will be a fiinite probability for particle to cross the barrier.

    Wave function of the particle in the region (x > 0) is

    

    So, probability of finding the particle in the region (v > 0) is