1.    This question consists of TWENTY FIVE sub-questions (1.1 to 1.25) of ONE mark each. For each of these sub-questions, four possible answers (a, b, c and d) are given, out of which only one is correct.

1.1.    If S is the closed surface enclosing a volume V and is the unit normal vector to the surface and is the positive vector, then the value of the following integral is

    (a) V

    (b) 2V

    (c) 0

    (d) 3V

Ans.    (d)

Sol.    

1.2.    For any operator A, i(A⁺ – A) is

    (a)    Hermitian

    (b)    anti-Hermitian

    (c)    unitary

    (d)    orthogonal

Ans.    (a)

Sol.    We know that,

    If A is Hermitian then it is equal to its complex conjugate transpose i.e.

    If A is anti-Hermitian then it is equal to its complex conjugate transpose with negative sign i.e.

    If A is unitary matrix then the conjugate transpose is equal to its inverse i.e.

    If A is orthogonal then the transpose of the matrix is equal to its inverse i.e.

    

1.3.    The value of the integral where C is the unit circle with the origin as the centre is

    (a) 0

    (b) z¹¹/11

    (c)

    (d) 1/11

Ans.    (a)

Sol.    f(z) = z¹⁰ is analytic everywhere in the complex argand plane.

    So, according to Cauchy integral theorem,

    

1.4.    Consider the set of vectors and

    (a)    The three vectors are orthonormal

    (b)    The three vectors are linearly independent

    (c)    The three vectors cannot form a basis in a three-dimensional real vector space

    (d)     can be written as a linear combination of and

Ans.    (b)

Sol.    

    

    So, are linearly independent.

1.5.    The Lagrangian for the Kepler problem is given by

        

    where denote the polar coordinates and the mass of the particle is unity. Then

    (a)

    (b)

    (c) the angular momentum of the particle about the centre of attraction is a constant

    (d) the total energy of the particle is time dependent

Ans.    (c)

Sol.    We have Lagrangian,

        

    Canonical momentum corresponding to coordinates

    Linear momentum,

    Equation of motion,

    Since, L does not depends on time explicitly. So, total energy of the system is conserved.

1.6.    Which of the following equations is relativistically invariant? ( and are constants of suitable dimensions)

    (a)

    (b)

    (c)

    (d)

Ans.    (b)

Sol.    Lagrangian transform,

    

    

    

    

    

1.7.    The Lagrangian for a three particle system is given by:

        

    where a is real. Then one of the normal coordinates has a frequency given by

    (a)

    (b)

    (c)

    (d)

Ans.    (c)

Sol.    We have lagrangian,

        

    

    Corresponding matrices,

    

    

    

    

1.8.    Two point charges Q₁ = 1nC and Q₂ = 2nC are kept in free space such that the distance between them is 0.1 m.

    (a)    The force on Q₂ is along the direction from Q₂ to Q₁

    (b)    The force on Q₂ is the same in magnitude as that on Q₁

    (c)    The force on Q₁ is attractive

    (d)    A point charge Q₃ = –3nC, placed at the midpoint between Q₁ and Q₂, experiences no net force

Ans.    (b)

Sol.    According to Coulomb's law, the force on Q₂ due to Q₁ is

        

    And the force on Q₁ due to Q₂ is

    

1.9.    A current I flows in the anticlockwise direction through a square loop of side a lying in the xoy plane with its centre at the origin. The magnetic induction at the centre of the square loop is

    (a)

    (b)

    (c)

    (d)

Ans.    (b)

Sol.    Magnetic field at distance from finite length wire is given by

    

    Therefore, the total magnetic field at the centre of square is given by

        

1.10.    A thin conducting wire is bent into a circular loop of radius r and placed in a time dependent magnetic field of magnetic induction.

        

    such that, the plane of the loop is perpendicular to . Then the induced emf in the loop is

    (a)

    (b)

    (c)

    (d)

Ans.    (a)

Sol.    The flux through the circular disc is

    

1.11.    Consider an electric field existing in the interface between a conductor and free space. Then the electric field is

    (a)    external to the conductor and normal to the conductor's surface

    (b)    internal to the conductor and normal to the conductor's surface

    (c)    external to the conductor and tangential to the conductor's surface

    (d)    both external and internal to the conductor and normal to the conductor's surface

Ans.    (a)

Sol.    For static charges field inside conductor is zero for all types of charge distribution.

    Using boundary condition

    

    Therefore, field is in the dielectric and perpendicular to surface of conductor.

1.12.    A spinless particle moves in a central potential V(r)

    (a)    The kinetic energy and the potential energy of the particle cannot simultaneously have sharp values

    (b)    The total energy and the potential energy of the particle can simultaneously have sharp values

    (c)    The total energy and the square of the orbital angular momentum about the origin cannot simultaneously have sharp values.

    (d)    The total energy of the particle can have only discrete eigenvalues

Ans.    (a)

Sol.    Kinetic energy of the particle is a function of its momentum and potential energy of the particle is a function of its position. According to Heisenberg's uncertainty principle, position and momentum of the particle cannot be measured simultaneously accurately. Therefore, kinetic energy and potential energy of the particle cannot simultaneously have sharp values.

    For a spinless particle of mass m moving in central potential V(r), the Hamiltonian of the system can be written as

        

    Therefore, , i.e., energy of the particle and square of the orbital angular momentum can simultaneously have sharp values.

1.13.    Which of the following functions represents acceptable wave function of a particle in the range .

    (a)

    (b)

    (c)

    (d)

Ans.    (d)

Sol.    For a particle moving in the range the acceptable wave function should be finite, single valued and continuous everywhere in space and the wave function should be square integrable in nature.

     is not finite at Therefore, the function is not acceptable.

     is not square integrable as

        

     is not finite at x = 0 (since D < 0)

     is finite, single valued and continuous everywhere in space. The function is also square integrable in nature as

        

1.14.    A quantum harmonic oscillator is in the energy eigenstate . A time independent perturbation acts on the particle, where is a constant of suitable dimensions and a and a^t are lowering and raising operators respectively. Then the first order energy shift is given by

    (a)

    (b)

    (c)

    (d)

Ans.    (c)

Sol.    First order energy shift due to perturbation

    =

1.15.    Two particles are said to be distinguishable when

    (a)    the average distance between them is large compared to their de Broglie wavelengths

    (b)    the average distance between them is small compared to their de Broglie wavelengths

    (c)    they have overlapping wavepackets

    (d)    their total wave function is symmetric under particle exchange

Ans.    (a)

Sol.    If the average distance between two particles is large compared to their de Broglie wavelengths, then the wave function of those particles will not overlap with each other i.e. two particles will be distinguishable.

1.16.    For an energy state E of a photon gas, the density of states is proportional to

    (a)

    (b) E

    (c) E^3/2

    (d) E²

Ans.    (d)

Sol.    The density of state in 3-D is

    

    Photons have two polarization state (One for each dimension transverse to the direction of propagation). So, g(E) should be multiplied by a factor of 2.

    

1.17.    X-rays were produced using Cobalt (Z = 27) as target. It was observed that the X-ray spectrum contained a strong line of wavelength 0.1785 nm and a weak line of wavelength 0.1930 nm. Then, the weak line is due to an impurity whose atomic number is

    (a) 25

    (b) 26

    (c) 28

    (d) 30

Ans.    (b)

Sol.    According to Moseley's law:

    

    Here, = characteristic frequency emitted by an element

        Z = atomic number of element

    Here, for strong 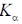line

        

    Here, we have used = 1 as screening factor

    and for weak line

    

    Now, from equations (ii) and (iii), we have

    

1.18.    A sample of Silicon of thickness 200 µm is doped with 10²³ Phosphorous atoms per m³. If the sample is kept in a magnetic field of 0.2 Wb/m² and a current of 1 mA is passed through the sample, the Hall voltage produced is

    (a)    62.5 µV

    (b)    –6.25 µV

    (c)    +6.25 µV

    (d)    –62.5 µV

Ans.    (d)

Sol.    Hall voltage is defined as:

    

    Where, B is magnetic field, I is current, t is the thickness, n is charge density and e is electronic charge.

    

    Here, in this question, the silicon is doped with phosphorus (P) which is pentavalent. therefore, the Hall voltage will be produced by electrons and will be of negative type.

1.19.    The probability that a state which is 0.2 eV above the Fermi energy in a metal atom at 700K is

    (a)    96.2%

    (b)    62.3%

    (c)    3.5%

    (d)    37.7%

Ans.    (c)

Sol.    The probability in Fermi-Dirac statistics is

    

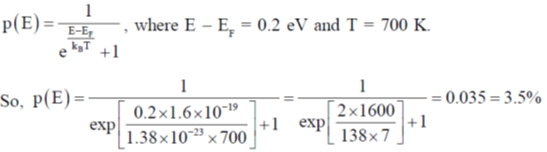
1.20.    The distance between the adjacent atomic planes in CaCO₃ is 0.3 nM. The smallest angle of Bragg scattering for 0.03 nm X-ray is

    (a)    2.9º

    (b)    1.5º

    (c)    0.29º

    (d)    5.8º

Ans.    (a)

Sol.    Here, interatomic distance, d = 0.3 nm

    Wavelength of X-ray is, = 0.03 nm

    From Bragg's law:

    

    

1.21.    Infrared absorption can be observed in which of the following molecules?

    (a)    N₂

    (b)    O₂

    (c)    HCl

    (d)    C₂

Ans.    (c)

Sol.    Since, we know that the infra-red absorption can be observed only on those molecules which have permanent dipole moment. In the above options, only HCl has permanent dipole moment.

1.22.    The cross-sections of the reactions and at a given energy are the same due to

    (a)    baryon number conservation

    (b)    time-reversal invariance

    (c)    charge conjugation

    (d)    parity conservation

Ans.    (c)

Sol.    Charge conjugation because both of these nuclear reactions are outcome of strong interaction. Due to charge conjugation particles and anti-particles have same rest mass which results in same cross-section.

1.23.    RAM and ROM are

    (a)    charge coupled devices used in computers

    (b)    computer memories

    (c)    logic gates

    (d)    binary counters used in computers

Ans.    (b)

Sol.    RAM (Random Access memory)

    ROM (Read Only Memory)

    Both are the computer memories.

1.24.    In an a-p-n transistor, the leakage current consists of

    (a)    electrons moving from the base to the emitter

    (b)    electrons moving from the collector to the base

    (c)    electrons moving from the collector to the emitter

    (d)    electrons moving from the base to the collector

Ans.    (d)

Sol.    For dc-biasing we apply input loop in forwards biased and output in reverse biased. When input loop is open still these have current in output loop. Which is represent by ICBO it is called leakage current also it is known as reverse saturation current of a reverse-biased diode.

    So, current will be flow from collector to base due to motion of electron from based to collectors.

1.25.    A piece of semiconducting material is introduced into a circuit. If the temperature of the material is raised, the circuit current will

    (a)    increase

    (b)    remain the same

    (c)    decrease

    (d)    cease to flow

Ans.    (a)

Sol.    As the temperature increases, the number of free electrons in the conduction band increases. So, conductivity of the semiconductor increases. So, in the circuit, current will increase as the temperature of the semiconductor is raised.

2.    This question consists of TWENTY FIVE sub-questions (2.1 to 2.25) of ONE mark each. For each of these sub-questions, four possible answers (a, b, c and d) are given, out of which only one is correct.

2.1.    

    (a) 1

    (b) 3

    (c) 0

    (d) –3

Ans.    (c)

Sol.    

    

2.2.    The value of the residue of is

    (a)

    (b)

    (c)

    (d)

Ans.    (b)

Sol.    Laurent series expansion of f(z) about z = 0, will be

    

    

2.3.    

    (a) f(x)

    (b) –f(x)

    (c) f(–x)

    (d) [f(x) + f(–x)]/2

Ans.    (c)

Sol.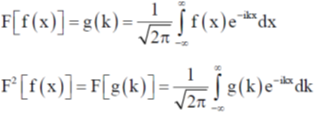    

    

2.4.    A particle of mass m is constrained to move on the plane curve xy = C(C > 0) under gravity (y axis vertical). The Lagrangian of the particle is given by

    (a)

    (b)

    (c)

    (d)

Ans.    (b)

Sol.    xy = C

    

    

    The kinetic energy of the particle is

    

    

    Therefore, the Lagrangian of the particle is given by

    

2.5.    If where is a scalar and [, ] denotes the

    (a)

    (b)

    (c)

    (d)

Ans.    (a)

Sol.    

    

2.6.    x and p are two operators which satisfy [x, p] = i. The operators X and P are defined as

     and for real. Then [X, Y] equals

    (a) 1

    (b) –1

    (c) i

    (d) –i

Ans.    (c)

Sol.    

2.7.    A quantum particle of mass m is confined to a square region in xoy-plane whose vertices are given by (0, 0), (L, 0), (L, L) and (0, L). Which of the following represents an admissible wave function of the particle (for l, m, n positive integers)?

    (a)

    (b)

    (c)

    (d)

Ans.    (c)

Sol.    For a quantum particle of mass m confined to a square region in x-y plane, the wave function of the particle should be zero at the boundary of the square for the sake of continuous nature of the wave function. Thus, the admissible wave function of the particle should satisfy the following condition:

    

    Only satisfies the above mentioned condition.

2.8.    Let denote the orbital angular momentum operators of a particle and let L₊ = L_x + iL_y and L_– = L_x – iL_y. The particle is in an eigenstate of L² and L_z eigenvalues and respectively. The expectation value of L₊ L_– in this state is

    (a)

    (b)

    (c) 0

    (d)

Ans.    (b)

Sol.    

    

2.9.    A normalized state of a particle moving in a potential V(x) is given by

    where 's are the normalized eigenfunctions of the particle corresponding to the energies E_n's. Then

    (a)

    (b) The average energy of the particle in the state is

    (c) is an eigenfunction of the Hamiltonian of the particle

    (d) is an eigenfunction of the momentum operator

Ans.    (a)

Sol.    For the given state of the particle to be normalized, the following condition should be satisfied:

    

    

    Average energy of the particle in the given state will be

    

     is not an eigen function fof the Hamiltonian of the particle only if ....all have same energy eigenvalues, i.e., the states are degenerate.

     is not an eigen function of the momentum operator as

    

2.10.    A coaxial cable of uniform cross-section contains an insulating material of dielectric constant 3.5. The radius of the central wire is 0.01 m and that of the sheath is 0.02 m. The capacitance per kilometer of a cable is

    (a)    280.5 nF

    (b)    28.05 nF

    (c)    56.10 nF

    (d)    2.805 nF

Ans.    (a)

Sol.    Capacitance of coaxial cable is per unit length

    

2.11.    The xoy plane carries a uniform surface current of density A/m. The magnetic field at the point z = –0.5m is

    (a) 10 × 10^–6 Wb

    (b) 1 × 10^–6 Wb

    (c)

    (d)

Ans.    (d)

Sol.    We know that magnetic field due to sheet carrying uniform current is given by

    

2.12.    Four point charges are placed at the corners of a square whose center is at the origin of a Cartesian coordinate system. A point dipole is placed at the centre of the square as shown in the figure. Then,

    (a) there is no force acting on the dipole

    (b) there is no torque about the centre of O on the dipole

    (c) the dipole has minimum energy if it is in direction

    (d) the force on the dipole is increased if the medium is replaced by another medium with larger dielectric constant

Ans.    (b)

Sol.    From figure we can say that there will be a net electric field along direction and field is not uniform.

    So, some force will act on the dipole.

    

    

    Force on dipole will decreases as dielectric constant is increased.

2.13.    The electric field E(t, t) at a point r at time t in a metal due to the passage of electrons can be described by the equation

        

    where is a characteristic associated with the metal and c is the speed of light in vacuum. The dispersion relation corresponding to the plane wave solutions of the form is given by

    (a)

    (b)

    (c)

    (d)

Ans.    (b)

Sol.    

    

2.14.    A copper wire of uniform cross-sectional area 1.0 × 10^–6 m² carries a current of 1A. Assuming that each copper atom contributes one electron to the electron gas, the drift velocity of the free electrons (density of copper is 8.94 × 10³ kg m³ and its atomic mass is 1.05 × 10^–25 kg) is

    (a)    7.4 × 10^–4 m/s

    (b)    74 × 10^–4 m/s

    (c)    74 × 10^–3 m/s

    (d)    7.4 × 10^–5 m/s

Ans.    (d)

Sol.    Free electron number density of the copper wire is

    

    We know that current density

    

    Also, J = nev, so, nev = 10º

    

2.15.    The number of hyperfine components observed in the electronic transition of an atom with nuclear spin is

    (a) 3

    (b) 4

    (c) 6

    (d) 5

Ans.    (a)

Sol.    

    The allowed values of hyperfine structure quantum number are

    F = |J + I|, |J + I – 1|, ....., |J – I|

    

    Thus, F = 1, 0

    Now, selection rule will gives transitions as shown in figure.

    Hence, total transitions are 3.

2.16.    Which of the following functions describes the nature of interaction potential V(r) between two quarks inside a nucleon? (r is the distance between the quarks and a and b positive constants of suitable dimensions)

    (a)

    (b)

    (c)

    (d)

Ans.    (b)

Sol.    Interaction potential can be given as

    

    where, because nuclear forces are short range and decreases with decreasing distance

        br because nuclear forces are repulsive at long range.

2.17.    Which of the following reactions violates lepton number conservation?

    (a)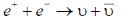

    (b)

    (c)

    (d)

Ans.    (c)

Sol.    For (a), = (–1 + 1) – (1 – 1) = (0) – (0) = 0

    For (b), = (1) – (1) = 0

    For (c), = (–1) – (1) = –2 violates lepton number conservation

    For (d), = (1) – (1) = 0 and = (0) – (0) = 0

2.18.    The Lande g-factor for the ³P₁ level of an atom is

    (a)    ½

    (b)    3/2

    (c)    5/2

    (d)    7/2

Ans.    (b)

Sol.    For ³p₁ term, l = 1, j = 1, 2s + 1 = 3 s = 1

    Therefore, Lande g-factor

    

2.19.    The pure rotational levels of a molecule in the far-infrared region follows the formula F(J) = BJ (J+1), where F(J) is the energy of the rotational level with quantum number J and B is the rotational constant. The lowest rotational energy gap in rotational Raman spectrum is

    (a)    2B

    (b)    4B

    (c)    6B

    (d)    8B

Ans.    (b)

Sol.    Selection rules of rotational Raman spectrum,

        

     = 0, corresponds to the Rayleigh line. However, = ±2, gives anti-Stokes line (–) and Stokes line(+) respectively.

    The wave number of the rotation Raman lines

    

    The rotation Raman shift

    

    For J = 0, 1, 2, 3,...., we get rotational Raman spectrum at distance 6B, 10B, 14B, 18B, .... with equidistant separation 4B.

2.20.    The total number of Zeeman components observed in an electronic transition of an atom in a weak field is

    (a) 4

    (b) 6

    (c) 12

    (d) 10

Ans.    (c)

Sol.    The electronic transitions of is shown in figure (below):

    The transitions with selection rules gives 12 Zeeman components in a weak field.

2.21.    A resistance of is parallel to an inductance of reactance applied voltage, then the total impedance of the circuit is

    (a)

    (b)

    (c)

    (d)

Ans.    (c)

Sol.    Total impedance of the circuit

    

    

2.22.    An n-channel silicon (dielectric constant = 12) FET with a channel width a = 2 × 10^–6 m is doped with 10²¹ electrons / m³. The pinch-off voltage is

    (a)    0.86V

    (b)    0.68V

    (c)    8.6V

    (d)    6.8V

Ans.

Sol.    The pinch-off voltage is given by

        

    q = 1.6 × 10^–19 Columb; N_D = Donor ions concentration = 10²³

    a = 2 × 10^–6 m (Depletion width)

    

    

    V_p = –3.01 Volt

    Note: None of the options given, is correct.

2.23.    The solution of the system of differential equations

        

    is given by (for A and B are arbitrary constants)

    (a) y(x) = Ae^3x + Be^–x; z(x) = –2Ae^3x + 2Be^–x

    (b)    y(x) = Ae^3x + Be^–x; z(x) = 2Ae^3x + 2Be^–x

    (c)    y(x) = Ae^3x + Be^–x; z(x) = 2Ae^3x – 2Be^–x

    (d)    y(x) = Ae^3x + Be^–x; z(x) = –2Ae^3x – 2Be^–x

Ans.    (a)

Sol.    

    Equation can be expressed as

        (D – 1)y + z = 0        ... (1)    [where, ]

        (D – 1)z + 4y = 0        ... (2)

    

    

    Let the trial solution y = e^mx

    

    

2.24.    If where f and g are arbitrary and twice differentiable functions, is a solution of the wave function

        

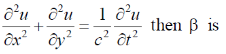
    (a)

    (b)

    (c)

    (d)

Ans.    (c)

Sol.    

    

    

    

    

    

    

2.25.    The rotational partition function for a diatomic molecule of moment of inertia I at a temperature T is given by

    (a)

    (b)

    (c)

    (d)

Ans.    (b)

Sol.    The rotational energy of a diatomic molecule of moment of inertia I is

     where is the quantum number associated to the rotation.

    The partition function is

    For large value of I and T, the energy separation between the levels is small and we can replace summation by integration. So the approximate rotational partition function is .

    

This section consists of TWENTY questions of FIVE marks each. ANY FIFTEEN out of these questions have to answered on the Answer Book provided.

3.    Given calculate the value of over the part of the sphere x² + y² + z² = 1 above the xoy plane.

Sol.    

    Using Divergence theorem

    

4.    Find the matrix of the linear transformation T on V₃(R) (i.e., three dimensional real vector space) defined as with respect to the basis where and . Also calculate the matrix representation of T^–1.

Sol.    

    

    

5.    Find the general solution of using the Frobenius power series method.

Sol.    

    Since, x = 0 is a regular singular point, we assume the solution,

    

    Putting these value in the above equation, we get,

    

    Now, equating the coefficient of the lowest power of x i.e. x^m–1 to be equal to zero

    

    Now, equating the coefficient of the x^m+k to be equal to zero

    

    

    

    

    

    

    

    

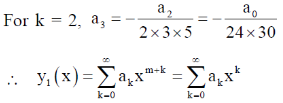
6.    Consider the Lagrangian where f(q) is an arbitrary function and .

    (a)    Write down the Euler-Lagrange equation of motion

    (b)    Does the Lagrangian transform covariantly under the transformation for a real constant?

    (c)    Calculate the Hamiltonian of the system

    (d)    Is total energy a constant of motion?

Sol.    (a)    

        The Euler-Lagrange equation,

        

        

        

        

    (b)    Since, L is a function of f(q), an arbitrary function, so the lagrangian does not transform covariantly under the transform

    (c)    

    (d)    Since, L does not depend on time explicitly. So, total energy of the motion is conserved.

7.    A square lamina OABC of side l and negligible thickness is lying in the XOY plane of a Cartesian coordinate system such that O is at the origin and the sides OA and OC are along the positive X and Y directions respectively. Calculate the moment of inertia tensor and the directions of the three principal moments. The mass of the lamina is m.

Sol.    

    

    Therefore, the moment of inertial tensor

        

    Let I₁, I₂ and I₃ are three principal moments of inertia.

    Therefore, the characteristic determinant,

        

    

    

    

    

    The principal axis is along

    Similarly, the principal axis corresponding to I₂ is along

    And the principal axis corresponding to I₃ is along

8.    A particle of mass m is subjected to a potential V(x) = Kx, K > 0

    (a)    If H is the Hamiltonian of the particle, calculate [H, V(x)]

    (b)    Use the uncertainty principle in the form to estimate the ground state energy of the particle.

Sol.    

    

    

    

    

9.    A particle of mass m in the one-dimensional energy well

        

    is in a state whose coordinate wave function is given by where c is the normalization constant.

    (a)    Determine the expectation value of the energy in the state

    (b)    Calculate the probability that on measurement of energy, the particle will be found in its ground state.

        

Sol.    

    According to normalization condition,

    

    

    

    (b)    The ground state of the particle in a box

        

    Therefore, the probability of finding the particle in the ground state is

    

     (using the standard integrals given in question)

    

10.    Consider the harmonic oscillator in the form H = (p² + x²)/2 (we have set m = 1, and ). The harmonic oscillator is in its nth energy eigenstate and subjected to a time-independent perturbation for real. Calculate the first-order energy shift and first-order correction to the wave function.

Sol.    

    The first order energy correction,

    

    

    The first order correction in wave function,

    

    

    

    

    

11.    An ideal electron gas is confined to an area A in a two-dimensional plane at temperature T. Calculate

    (a)    the density of states

    (b)    N, the number of electrons

    (c)    EF, the Fermi energy as a function of N

Sol.    Density of states,

    The probability that the quantum state of wave-vector k is occupied by an electron is given by the Fermi-Dirac distribution function

    

    

    Facto of 2 comes from two spins of electron

        

    And we know,

    

    At T = 0K,

    

    

12.    Write down the partition function of a particle of mass m whose potential energy is given by

    V(x, y, z) = ax² + b(y² + z²)^1/2, where a and b are positive constants of suitable dimensions. Also calculate the average energy of the particle.

        

Sol.    The total energy is

    

    

    

    

    

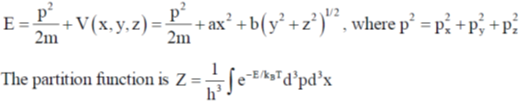
    The average energy of the particle is

    

13.    Given that the molecular weight of KCl is 74.6 and its density is 1.99 × 10³ kg/m³, calculate the following:

    (a)    the distance between the atomic planes

    (b)    the lattice constant

Sol.    (a)    The interplanar distance of atomic plane (1 0 0)

        

    The interplanar distance of atomic plane (1 1 0)

        

    The interplanar distance of atomic plane (1 1 1)

        

    (b)    KCL has fcc structure, so the number of atoms in the unit cell is n = 4

    The lattice constant of the KCL crystal,

    

14.    The reaction ³H(p, n)²He has a Q value of –0.764 MeV. Calculate the threshold energy of incident protons for which neutrons are emitted in the forward direction.

Sol.    We know the threshold energy,

    Given: Q = –0.764 MeV

        m_x = (2p) = 2 × 1.00814 = 2.01628 amu

        M_x = M(³H) = 3.0169982 amu

    Therefore, the threshold energy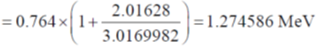

15.    A circular conducting loop C₁ of radius 2m is located in the XOY plane such that its centre is at (0, 0, 0). Another circular conducting loop C₂ of radius 2m is located at (0, 0, 4) such that the plane of C₂ is parallel to the XOY plane. A current of 5A is flowing in each of these loops such that the positive Z-axis lies to the left of the directions of the currents. Find the magnetic induction produced at (0, 0, 0), neglecting the mutual induction of the loops.

Sol.    The magnetic field at z = 0 due current flow in the loop C₂ is

    

    

    The magnetic field at (0, 0, 0) due to current flow in he loop C₁ is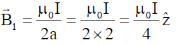

    So, total magnetic field at z = 0

    

16.    Draw the electrical circuits for each of the following source (battery), a detector (lamp), and switch (es).

    (a) AND

     (b) OR

    (c) NOT

    (d) NAND

    (e) NOR

Sol.    

    

    

    

    

17.    The pinch-down voltage of a p-channel junction FET is V_P = 5V and the drain-to-source saturation current I_DSS = –40mA. The value of drain-source voltage V_DS is such that the transistor is operating in the saturated region. The drain current is given as I_D = –15 mA. Find the gate-source voltage V_GS.

Sol.    Given: pinch-off voltage, V_P = 5V

    Drain to source saturation current, I_DSS = –40 mA

    Drain current, _ID = –15 mA

    

    

    

18.    A narrow beam of electrons, accelerated under a potential difference, incident on a crystal whose grating space is 0.3 nm. If the first diffraction ring is produced at an angle 5.8º from the incident beam, find the momentum of the electrons and the potential difference applied.

Sol.    

    

19.    The region z > 0 of a Cartesian coordinate system contains a linear isotropic dielectric of dielectric constant 2.0. The region z < 0 is the free space. A free space charge density of 5nC/m² is at the interface z = 0. If the displacement vector in the dielectric is nC/m², find the corresponding displacement vector in the free space.

Sol.    Let us take z < 0 as regionl and z > 0 as region 2

    According to boundary condition,

    

    

    

    

20.    The series limit of the Balmer series for hydrogen atom is given as 360 nm. Calculate the atomic number of the element that gives the lowest x-ray wavelength at 0.1 nm of the K-series.

Sol.    

    By Moseley's law:

    

    

21.    The first few electronic energy states for neutral copper atom (Z = 29) are given as E₁ < E₂ < E₃, where E₁ being the ground electronic state. The states E₂ and E₃ are doubly degenerate due to spin splitting. Write the electron configuration of the states and arrange the spectral terms of the split levels following Hund's rules. Explain why E₂ < E₃.

Sol.    Cu(Z = 29) = [Ar] 3d¹⁰4s¹ = Ground state electronic configuration

    First excited state of Cu = [Ar]3d¹⁰4s⁰4p¹

    Second excited state of Cu = [Ar]3d¹⁰4s⁰4p⁰4s⁰4p¹

    First and second states are written keeping in mind the selection rule

    Ground state energy = E₁

    First excited state = E₂

    Second excited state = E₃

    

    

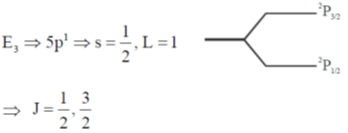
    State E₂ and E₃ are doubly degenerate (because of splitting) E3 corresponds to principal quantum number, n = 5, while E₂ corresponds to n = 4. So, E₃ has higher n value. That's why energy of E₃ will be more than energy of E₂(E₂ < E₃).

22.    The rotational lines of the CN band system at 3883.4Å is represented by a formula = (25798 + 3.850m + 0.068 m²) cm^–1, where m is a running number. Calculate the values of the rotational constants and , the location of the band head and the degradation of the band.

Sol.    The given rotational line

        

    We know that the lines of P and R branches of a band are represented by a single formula

        

    Comparing it with the given equation, we have

    

    

    Now, the m value corresponding to the vertex of the Fortrat parabola (band-head) is given by

        

    Therefore, the band head

    The band head (25744 cm^–1) lies toward the lower frequency side of the band origin (25798 cm^–1). This means that the band is degraded toward the high-frequency side, that is toward the violet-degraded band.