1. An object is dropped on a cushion from a height 10m above it. On being hit, the cushion is depressed by 0.1m. Assuming that the cushion provides a constant resistive force, the deaccelerate of the object after hitting the cushion, in terms of the acceleration due to gravity g, is

(a) 10 g

(b) 50 g

(c) 100 g

(d) g

Ans. (c)

Sol.

Equation of motion

v² – u² = 2aS ... (3)

Eq. (1), (2) put in Eq. (3)

2. A turn-table is rotating with a constant angular velocity . In the rotating frame fixed to the turn-table, a particle moves radially outwards at a constant speed v₀. The acceleration of the particle in the r-coordinates, as seen from an inertial frame, the origin of which is at the centre of the turn-table, is

(a)

(b)

(c)

(d)

Ans. (d)

Sol. We know that acceleration in polar coordinate is

Eq. (2), (3) put in Eq. (1)

3. Assume that the earth revolves in a circular orbit around the sun. Suppose the gravitational constant G varies slowly as a function of time. In particular, it decreases to half its initial value in the course of one million years. Then during this time the

(a) radius of the earth's orbit will increase by a factor of two.

(b) total energy of the earth remains constant.

(c) orbital angular momentum of the earth will increase.

(d) radius of the earth's orbit remains the same.

Ans. (a)

Sol. The orbital angular momentum of the earth is conserved for circular motion.

Total energy of the earth is not constant.

4. A particle of mass m moves in one dimension in the potential V(x) = kx⁴, (k > 0). At time t = 0, the particle starts from rest at x = A. For bounded motion, the time period of its motion is

(a) proportional to A^–1/2

(b) proportional to A^–1

(c) independent of A

(d) not well-defined (the system is chaotic)

Ans. (b)

Sol. For V(x) = kxⁿ

5. The infinite square-well potential of a particle in a box of size a is modified as shown in the figure below (assume << a)

The energy of the ground state, compared to the ground state energy before the perturbation was added

(a) increases by a term of order

(b) decreases by a term of order

(c) increases by a term of order

(d) decreases by a term of order

Ans. (d)

Sol. The normalized ground state wave function of a particle in a 1-D infinite potential box of the width a given by

Given: Perturbing potential

The first order energy correction in the ground state energy, will be

The second order energy correction in the ground state energy, will be

6. A quantum particle of mass m in one dimension, confined to a rigid box as shown in the figure, is in its ground state. An infinitesimally thin wall is very slowly raised to infinitely at the centre of the box, in such a way that the system remains in its ground state at all times. Assuming that no energy is lost in raising the wall, the work done on the system when the wall is fully raised, eventually separating the original box into two compartments, is

(a)

(b)

(c)

(d) 0

Ans. (a)

Sol. The energy spectrum of the 1-D symmetric infinite potential well of width '2L' is,

where (n-1) represents the number of nodes [excluding the nodes at the boundary] in the particular energy eigenstate.

In the old ground state, there are no nodes. So, ground state corresponds to n = 1 and old ground state energy will be

In the new ground state, there is one node at x = 0. So, ground state corresponds to n = 2 and new ground state energy will be

7. The wavefunction of a free particle of mass m, constrained to move in the interval –L < x < L, is = A(L + x)(L – x), where A is the normalization constant. The probability that the particle will be found to have the energy is

(a) 0

(b)

(c)

(d)

Ans. (a)

Sol. Given wavefunction of the particle: , which has an even parity.

The energy spectrum of the 1-D symmetric infinite potential well of width '2L' is,

corresponds to n = 2 (1st excited state of the potential well).

The wave function of the particle in the 1st excited state of the potential well, is

which has an odd parity.

The probability that the particle will be found to have energy is

[As the integrand is an odd function]

8. A particle moving in a central potential is described by a wavefunction = zf(r), where r = (x, y, z) is the position vector of the particle and f(r) is a function of r = |r|. If L is the total angular momentum of the particle, the value of L² must be

(a)

(b)

(c)

(d)

Ans. (a)

Sol. Given wavefunction of the particle:

Here, angular part of the wavefunction is, [where spherical harmonics ]

Therefore, l = 1 for the given state of the particle.

9. A particle of mass m and energy E > 0, in one dimension is scattered by the potential shown below.

If the particle was moving from x = – to x = , which of the following graphs gives the best qualitative representation of the wavefucntion of this particle?

(a)

(b)

(c)

(d)

Ans. (c)

Sol. Since, energy of the particle is constant and V_b < V_a, therefore T_b > T_a.

The kinetic energy of the particle at a point is related to velocity of the particle at that point. Higher the velocity of the particle at any point, lesser is the probability finding the particle there.

Since, T_b > T_a, therefore,

Here, kinetic energy (T) is more in the region a < x < b. So, wavelength will less in that region.

Only option (c) satisfies both conditions.

10. Consider a planar wire loop as an n-sided regular polygon, in which R is the distance from the centre to a vertex. If a steady current I flows through the wire, the magnitude of the magnetic field at the centre of the loop is

(a)

(b)

(c)

(d)

Ans. (d)

Sol. Magnetic field at centre due to one side is

Therefore, the net magnetic field at the centre will be

11. Two coherent plane electromagnetic waves of wavelength 0.5 µm (both have the same amplitude and are linearly polarized along the z-direction) fall on the y = 0 plane. Their wave vectors k₁ and k₂ are as shown in the figure.

If the angle is 30º, the fringe spacing of the interference pattern produced on the plane is

(a) 1.0 µm

(b) 0.29 µm

(c) 0.58 µm

(d) 0.5 µm

Ans. (d)

Sol.

Now, for m^th order maxima

Therefore, the fringe width

12. Which of the following is not a correct boundary condition at an interface between two homogeneous dielectric media? (In the following is a unit vector normal to the interface, and j_s are the surface charge and current densities, respectively).

(a)

(b)

(c)

(d)

Ans. (a)

Sol. The correct option is (a).

13. The permittivity tensor of a uniaxial anisotropic medium, in the standard Cartesian basis, is

, where is a constant.

The wave number of an electromagnetic plane wave polarized along the x-direction, and propagating along the y-direction in this medium (in terms of the wave number k₀ of the wave in vacuum) is

(a) 4k₀

(b) 2k₀

(c) 9k₀

(d) 3k₀

Ans. (b)

Sol.

14. The elements of a 3 × 3 matrix A are the products of its row and column indices A_ij = ij (where i, j = 1, 2, 3). The eigenvalues of A are

(a) (7, 7, 0)

(b) (7, 4, 3)

(c) (14, 0, 0)

(d)

Ans. (c)

Sol.

Method 1:

Characteristic equation of matrix A:

Method 2:

For the given matrix A, the 2^nd & 3^rd row are scalar multiples of 1^st row [Rows are scalar multiple of a particular row] and 2^nd & 3^rd column are scalar multiples of 1^st column [Columns are scalar multiples of a particular column]. For this type of matrices, one of the eigenvalues will be equa to the trace of the matrix and other eigenvalue will be equal to zero.

Therefore, eigenvalues of the given matrix will be 14,0, 0.

15. In the following circuit, each device D may be an insulator with probability p, or a conductor with probability (1 – p).

The probability that a non-zero current flows through the circuit is

(a) 2 – p – p³

(b) (1 – p)⁴

(c) (1 – p)² p²

(d) (1 – p) (1 – p³)

Ans. (d)

Sol. Suppose, the three devices (connected in parallel) are denoted by D₁, D₂ and D₃ respectively and the fourth device (connected in series) is denoted by D₄.

There will be non-zero current flow through the circuit, if current passes through at least one of the devices D₁, D₂, D₃ and through the device D₄.

Therefore, P(Non-zero current flow)

= P(Current flow through at least one of D₁, D₂, D₃) × P(Current flow through D₄)

= [1 – P(No current flow through D₁, D₂ & D₃)] × P(Current flow through D₄)

= [1 – P(All of D₁, D₂ & D₃ are insulators)] × P(D₄ is a conductor)

= [1 – p³] (1 – p)

16. The solution of the differential equation with the boundary condition y(x = 1) = 0, is

(a)

(b)

(c)

(d) (x – 1)²e^–x

Ans. (a)

Sol.

It is a first order linear differential equation of the following form:

Applying the given condition y(x = 1) = 0, one can obtain C = –1.

Therefore, the solution will be

17. The value of the definite integral is

(a)

(b)

(c)

(d)

Ans. (d)

Sol.

Therefore, required integral:

18. In a system comprising of approximately 10²³ distinguishable particles, each particle may occupy any of 20 distinct states. The maximum value of the entropy per particle is nearest to

(a) 20 k_b

(b) 3 k_B

(c) 10(ln 2)k_B

(d) 20(ln 2)k_B

Ans. (b)

Sol. For N distinguishable particles when g states are available to each particle, the maximum value of entropy per particle is

S = k_B ln g = k_B ln 20

S = 2.99 k_B = 3k_B

19. Consider a classical gas in thermal equilibrium at temperatures T₁ and T₂. Which of the following graphs correctly represents the qualitative behaviour of the probability density function of the x-component of the velocity?

(a)

(b)

(c)

(d)

Ans. (c)

Sol. The probability density function of the x-component of the velocity of molecules of a classical gas is , where

="text-align: justify; margin-left: 54pt;"> (a) As the temperature of the gas increases. The velocity of the gas molecules will increase. This causes the broadening of the curve.

(b) Since the total area under the curve, i.e.,

, the broadening of the curve will peak the curve down.

20. The equation of state of an ideal gas is pV = RT. At very low temperatures, the volume expansion coefficient at constant pressure

(a) diverges as 1/T²

(b) diverges as 1/T

(c) vanishes as T

(d) is independent of the temperature

Ans. (b)

Sol. The volume expansion coefficient is

21. The Hamiltonian of a classical nonlinear one dimensional oscillator is , where > 0 is a constant. The specific heat of a collection of N independent such oscillators is

(a)

(b)

(c) Nk_B

(d)

Ans. (b)

Sol. Given hamiltonian is

Using general law of equipartition of energy, we have

Therefore, total average thermal energy is

Therefore, specific heat is given by

22. In an experiment to measure the acceleration due to gravity g using a simple pendulum, the length and time period of the pendulum are measured to three significant figures. The mean vlaue of g and the uncertainty of the measurements are than estimated using a claculator from a large number of measurements and found to be 9.82147 m/s and 0.02357 m/s², respectively. Which of the following is the most accurate way of presenting the experimentally determined value of g?

(a) 9.82 ± 0.02 m/s²

(b) 9.8215 ± 0.02 m/s²

(c) 9.82147 ± 0.02357 m/s²

(d) 9.82 ± 0.02357 m/s²

Ans. (a)

Sol. We have g = 9.82147 m/s² and = 0.02357 m/s²

The most accurate way of presenting the value of g.

g = 9.82 + 0.02 m/s²

23. An ac signal of the type as shown in the figure, is applied across a resistor R = .

The power disipated across the resistor is

(a) 12.5 W

(b) 9 W

(c) 25 W

(d) 21.5 W

Ans. (d)

Sol.

Therefore, the power dissipated across the resistor

24. An npn-transistor is connected in a voltage divider configuration as shown in the figure below.

If the resistor R₂ is disconnected, the voltages V_B at the base and V_C at the collector change as follows.

(a) Both V_B and V_C increase

(b) Both V_B and V_C decrease

(c) V_B decreases, but V_C increase

(d) V_B increases, but V_C decreases

Ans. (d)

Sol. Before disconnect the R₂ the equivalent circuit is given below:

Applying KVL in input loop, we can write

Now, after remove the R₂ the equivalent circuit is given below:

Applying KVL in input loop,

I_C = 50 × 0.147 = 7.35 mA

As I_C is increase so V_C will decrease.

25. Let Y denote the output in the following logical circuit.

If , the gates G₁ and G₂ must, respectively, be

(a) OR and NAND

(b) NOR and OR

(c) AND and NAND

(d) NAND and OR

Ans. (b)

Sol.

26. A solid spherical cork of radius R and specific gravity 0.5 floats on water. The cork is pushed down so that its centre of mass is at a distance h (where 0 < h < R) below the surface of water, and then released. The volume of the part of the cork above water level is , where is the angle as shown in the figure.

At the moment of release, the dependence of the upward force on the cork on h is

(a)

(b)

(c)

(d)

Ans. (a)

Sol.

F_net = F_b – mg

V_w = volume of water displaced

Eq. (2), (3), (4) put in Eq. (1)

27. Two particles of masses m₁ and m₂ are connected by a massless thread of length as shown in figure below.

The particle of mass m₁ on the plane undergoes a circular motion with radius r₀ and angular momentum L. When a small radial displacement (where << r₀) is applied, its radial coordinate is found to oscillate about r₀. The frequency of the oscillations is

(a)

(b)

(c)

(d)

Ans. (d)

Sol. Equations of motion of m₁ and m₂ are:

Eliminating T from Eq. (1) and Eq. (2), we get

Substituting Eq. (7) in Eq. (5), we get

28. The time evolution of a coordinate x of a particle is described by the equation:

For > A, the particle will

(a) eventually come to rest at the origin

(b) eventually drift to infinity

(c) oscillate about the origin

(d) eventually come to rest at /A or –/A

Ans. (c)

Sol. Given:

Assume a trial solution, x = Ae^mt

Auxiliary equation of the given differential equation, will be

Therefore, the solution will be

All the terms in the above expression are oscillatory in nature.

Therefore, the particle will oscillate about the origin.

29. The Hamiltonian of a quantum particle of mass m is , where and r are positive constants. The energy E_n of the n^th level, for large n, depends on n as

(a) n^2r

(b) n^{r + 2}

(c) n^{1/(r + 2)}

(d) n^{2r/(r + 2)}

Ans. (d)

Sol. According to WKB Approximation method, if then energy of the n^th level will be

For large values of n,

30. In the particle wave expansion, the differential scattering cross-section is given by

where is the scattering angle. For a certain neutron-nucleus scattering, it is found that the two lowest phase shifts and corresponding to s-wave and p-wave, respectively, satisfy . Assuming that the other phase shifts are negligibly small, the differential cross-section reaches its minimum for cos equal to

(a) 0

(b) ±1

(c)

(d)

Ans. (c)

Sol.

Considering only the s and p wave scattering, we can write,

31. A charged, spin-less particle of mass m is subjected to an attractive potential

, where k is a positive constant.

Now a perturbation in the form of a weak magnetic field (where B₀ is a constant) is switched on. Into how many distinct levels will the second excited state of the unperturbed Hamiltonian split?

(a) 5

(b) 4

(c) 2

(d) 1

Ans. (a)

Sol. The perturbation is,

Now, the second excited state is six-fold degenerate

Therefore, the parturbation matrix is,

Characteristic equation of the perturbation matrix

Therefore, the matrix has five distinct eigenvalues,

Therefore, the second excited state will split into 5 different lines.

32. The elastic scattering of a charged particle of mass m off an atom can be approximated by the potential , where and R are positive constants. If the wave number of the incoming particle is k and the scattering angle is 2, the differential cross-section in the Born approximation is

(a)

(b)

(c)

(d)

Ans. (d)

Sol. Given scattering potential , is spherically symmetric in nature.

According to First Born Approximation, the scattering amplitude for a spherically symmetric potential is,

33. The wave number k and the angular frequency of a wave are related by the dispersion relation , where and are positive constants. The wave number for which the phase velocity equals the group velocity, is

(a)

(b)

(c)

(d)

Ans. (b)

Sol.

Given: Group Velocity (v_g) = Phase Velocity (v_p)

34. An inertial observer A at rest measures the electric and magnetic field E = (, 0, 0) and B = (, 0, 2) in a region, where a is constant. Another inertial observer B, moving with a constant velocity with respect to A, measures the field as and . Then, in units c = 1, E'_x and B'_y are given, respectively, by

(a)

(b)

(c)

(d)

Ans. (d)

Sol. remains invariant under the Lorentz transformation.

Also, E² – c²B² remains invariant under the Lorentz transformation.

From Eq. (1) and Eq. (2), we get

35. A point charge is moving with a uniform velocity along the positive x-direction, parallel to and very close to a corrugated metal sheet (see the figure below).

The wavelength of the electromagnetic radiation received by an observer along the direction of motion is

(a)

(b)

(c)

(d) L

Ans. (*)

Sol. The frequency of dipole oscillation in its rest frame is

Therefore, the frequency of radiation in the rest frame of the particle is

Therefore, the frequency of the radiation with respect to observer in lab frame will be

Therefore, the wave length respect to observer

36. If the newton-Raphson method is used to find the positive root of the equation x = 2 sin x, the iteration equation is

(a)

(b)

(c)

(d)

Ans. (b)

Sol. Given equation: x = 2sin x x – 2sin x = 0

Iteration equation according to Newton-Raphson method will be

37. The equation of motion of a forced simple harmonic oscillator is , where A is a constant. At resonance the amplitude of oscillations at large times

(a) saturates to a finite value

(b) increases with time as

(c) increases linearly with time

(d) increases exponentially with time

Ans. (c)

Sol. Given: Equation of motion of a forced harmonic oscillator is

It is 2^nd order linear non-homogeneous differential equation with constant co-efficients.

Complementary function of the differential equation will be

Particular integral of the differential equation will be

The general solution of the given differential equation at resonance

Therefore, the amplitude of oscillation will increase linearly with time.

38. The operator A has a matrix representation in the basis spanned by and . In another basis spanned by , the matrix representation of A is

(a)

(b)

(c)

(d)

Ans. (b)

Sol. We can check that the new basis vector are eigenvectors of the operator with eigenvalues 3 and 1 respectively.

Therefore, in the new basis, the operator A will be represented by a diagonal matrix whose principal diagonal element will be equal to the eigenvalues of the operator A. So, the matrix representation of the operator A in the new basis, will be .

39. The operator , where is the Dirac delta function, acts on the space of real-valued square-integrable functions on the real line. This operator is equivalent to

(a)

(b)

(c) x

(d) 0

Ans. (a)

Sol.

40. At each time step, a random walker in one-dimension either remains at the same point with probability ¼, or moves by a distance to the right or left with probabilities 3/8 each. After N time steps, its root mean squared displacement is

(a)

(b)

(c)

(d)

Ans. (c)

Sol. Probability distribution corresponding to the displacement in the given I-D random walk problem, is

Mean displacement of random walker

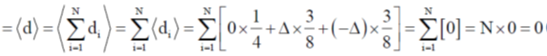
Mean squared displacement of the random walker

[Since, the probability of movement toward right and left are same, therefore the contribution of the second term will be zero]

Root mean squared displacement of the random walker

41. The Hamiltonian of three Ising spins S₁, S₂ and S₃, each taking values ±1, is H = –J(S₁S₂ + S₂S₃) –hS₁, where J and h are positive constants. The mean value of S₃ in equilibrium at a temperature T = 1/(k_B), is

(a)

(b)

(c)

(d) 0

Ans. (b)

Sol. The possible value of energies are:

42. The free energy of a magnetic system, as a function of its magnetisation m, is , where a and b are positive constants. At a fixed value of a, the critical value of b, above which the minimum of will be at a non-zero value of magnetisation, is

(a)

(b)

(c)

(d)

Ans. (b)

Sol.

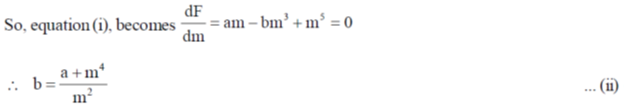
At critical point, the minimum value of free energy for non-zero value of magnetization m coincide with the value of free energy at m = 0. For critical value of b,

Putting equation (ii) in (i), we get

On solving, we get

Putting equation (iii) in equation (ii), we get

43. For optimal performance of an op-amp based current-to-voltage converter circuit, the input and output impedance should be

(a) low input impedance and high output impedance

(b) low input impedance and low output impedance

(c) high input impedance and high output impedance

(d) high input impedance and low output impedance

Ans. (b)

Sol.

This is negative voltage to current feedback amplifier circuit.

Therefore, for optimal performance of an op-amp based current to voltage converter circuit, both input and output impedance will be low.

44. The forward diode current is given by , where E_g is the band gap of the semiconductor, V is the voltage drop across the diode, T is the temperature of the diode operating near room temperature and and are constants. A diode is used as a thermal sensor in the circuit shown below.

If V is measured using an ideal voltmeter to estimate T, the variation of the voltage V as a function of T is best approximated by (in the following a and b are constants)

(a) aT² + b

(b) aT + b

(c) aT³ + b

(d) aT + bT²

Ans. (b)

Sol.

In forward biased I >> I₀

Since, current source has been used.

45. A circuit constructed using op-amp, resistor R₁ = 1 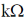and capacitors C₁ = 1 µF and C₂ = 0.1 µF, is shown in the figure below.

This circuit will act as a

(a) high pass filter

(b) low pass filter

(c) band pass filter

(d) band reject filter

Ans. (a)

Sol. Transfer function of this circuit

Therefore, the given circuit will behave like a high pass filter.

46. The third-nearest neighbour distance in a BCC (Body Centered Cubic) crystal with lattice constant a₀ is

(a) a₀

(b) 3a₀/2

(c)

(d)

Ans. (d)

Sol.

1^st nearest neighbour distance is

2^nd nearest neighbour distance is = a₀

3^rd nearest neighbour distance is

47. A bound electron and hole pair interacting via Coulomb interaction in a semiconductor is called an exciton. The effective masses of an electron and a hole are about 0.1 m_e and 0.5 m_e respectively, where m_e is the rest mass of the electron. The dielectric constant of the semiconductor is 10. Assuming that the energy levels of the excitons are hydrogen like, the binding energy of an exciton (in units of the Rydberg constant) is closest to

(a) 2 × 10^–3

(b) 2 × 10^–4

(c) 8 × 10^–4

(d) 3 × 10^–3

Ans. (c)

Sol.

= –0.0008333 × R = –(8.33 × 10^–4) × R

Thus, the ground state energy of exciton = –8.33 × 10^–4 R

Hence, the binding energy exciton is 8.33 × 10^–4 (in units of Rydberg constant)

48. Consider an array of atoms in one dimension with an ensemble averaged periodic density distribution as shown in the figure.

If k is the wave number and S(k, ) denotes the Fourier transform of the density-density correlation function, the ratio S(k,)/S(k, 0) is

(a)

(b)

(c)

(d)

Ans. (d)

Sol. The density distribution can be written as:

49. A doubly charged ion in the angular momentum state (J = 2, J₃ = 1) meets a gas of polarized electrons (S₃ = 1/2) and gets neutralized. If the orbital angular momentum transferred in the process is zero, the probability that the neutral atom is in the (J = 2, J₃ = 2) state is

(a) 2/5

(b) 2/3

(c) 1/5

(d) 1/3

Ans. (d)

Sol. Let doubly charged ion is A⁺⁺, the reaction followed by A⁺⁺ is given by

For A⁺⁺ : J₁ = 2, (J₃)₁ = M₁ = 1 (Given)

For A: J = 2, J₃ = M = 2 (Given)

For the calculation of probability that the neutral atom is in the J = 2, m = 2 state, we will first calculate Clebsch-Gordan coefficient for J₁ = 2, M₁ = 1, J₂ = 1, M₂ = 1, J = 2, M = 2

The clebsch-Gordan coefficients are the solutions to

Explicitly:

The summation is extended over allinteger k for which the argument of every factorial is non-negative.

Now, for the question, C.G. coefficient =

[The summation is extended for only k = 1, because othervalues of k makes factorial negative]

The probability of finding neutral particle (A) into J = 2, M = 2 (=J₃) state

50. The rang of the inter-atomic potential in gaseous hydrogen is approximately 5Å. In thermal equilibrium, the maximum temperature for which the atom-atom scattering is dominantly s-wave, is

(a) 500 K

(b) 100 K

(c) 1 K

(d) 1 mK

Ans. (c)

Sol. In atomic-atomic scttering s-2ave will dominate, if

where T is the temperature, m is the mass of hydrogen atom = 1.67 × 10^–27 kg,

k_B is Boltzmann constant = 1.38 × 10^–23 J/K,

R_eff is interatomic potential range = 5 Å

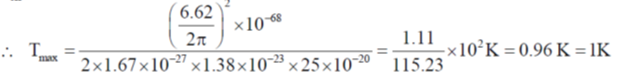
51. The energy levels corresponding to the rotational motion of a molecule are E₃ = BJ(J + 1)cm^–1 where J = 0,1,2, ..... and B is a constant. Pure rotational Raman transitions follow the selection rule = 0, ±2. When the molecule is irradiated, the separation between the closest Stokes and anti-Stokes lines (in cm^–1) is

(a) 6 B

(b) 12 B

(c) 4 B

(d) 8 B

Ans. (b)

Sol. Since E_J = BJ(J + 1) and selection rule is = 0, ± 2.

So, Raman displacement for pure rotational Raman is calculated as

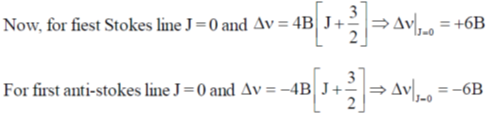
Then separation between closest Stokes and Anti-Stokes line is 6B – (–6B) = 12 B.

52. The cavity of a He-Ne laser emitting at 632.8 nm, consists of two mirrors separated by a distance of 35 cm. If the oscillations in the laser cavity occur at frequencies within the gain bandwidth of 1.3 GHz, the number of longitudinal modes allowed in the cavity is

(a) 1

(b) 2

(c) 3

(d) 4

Ans. (c)

Sol. = 632.8 nm and distance between two mirros d = 35 cm, gain bandwidth  = 1.3 GHz.

Number of longitudinal modes

[where n₀ is refractive index of medium which is considered as 1]

53. An excited state of a nucleus decays into two  particles which are in a spin-parity 0⁺ state. If the mean life-time of this decay is 10^–22 s, the spin-parity of the excited state of the nucleus is

(a) 2⁺

(b) 3⁺

(c) 0^–

(d) 4^–

Ans. (a)

Sol.

Life time of this decay is 10^–22 sec. Thus, it proceeds via strong interaction. Angular momentum and parity is conserved.

If the orbital angular momentum carried by alpha particles is , then for conservation of angular momentum.

Now, for parity conservation,

, where parity of Be and  particle are P_Be and P_He. Since, parity of  particles are even.

Thus, if P_Be is odd, then to conserve parity.

If P_Be is even, then to conserve parity and from equation (i), . This is only satisfied by 2⁺.

54. The elastic scattering of a neutrino v_e by an electron e^–, i.e. the reaction , can be described by the interaction Hamiltonian .

The cross-section of the above process depends on the centre of mass energy E, as depends on the centre of mass energy E, as

(a) 1/E²

(b) E²

(c) E

(d)

Ans. (b)

Sol. The variation of the cross-section of the elastic scattering of a neutrino _e by an electron (e^–1) with centre of mass energy is given by

55. The mean life-time of the following decays:

(a)

(b)

(c)

(d)

Ans. (c)

Sol. Reaction: , is governed via strong interaction (lifetime < 10^–21 seconds)

Reaction: , is governed via electromagnetic interaction (life : 10^–20 to 10^–16 seconds)

Reaction: , is governed via weak interaction (life : 10^–13 to 10³ second)

Thus,