1. Consider the three vectors and where and are the standard unit vectors in three – dimensional Euclidean space. These vectors will be linearly dependent of the value of is

(a)

(b)

(c)

(d) 0

Ans. (a)

Sol.

2. The Fourier transform of the function f(x) = e^–|x| is

(a)

(b)

(c)

(d)

Ans. (c)

Sol. Fourier transform of the function f(x) = e^–|x| is

Short Trick: for the given question, a = 1. We can use this standard result also.

3. The value of the integral is

(a) 0

(b)

(c)

(d) 1

Ans. (b)

Sol. Property of Dirac Delta Function:

where x'_i s are the zeroes of the function f(x)

Using the property, we can write,

Therefore, the integral,

Property of Dirac Delta fucntion:

Using the property, we can write,

4. Consider the following ordinary differential equation with the boundary conditions x (t = 0) = 0 and x (t = 1) = 1. The value of x (t) at t = 2 is

(a)

(b)

(c)

(d)

Ans. (c)

Sol.

Replacing all these in the equation (1), we will get

It is a second order linear differential equation

Assuming a trial solution, z = Ce^mt and replacing in equation (2) will be get

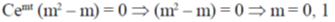
Therefore, the solution will be of the form

Applying the given condition, i.e. x(0) = 0, x(1) = 1, we will get

5. What is the value of for which is an analytic function of complex variable z = x + iy?

(a) 1

(b) 0

(c) 3

(d) 2

Ans. (a)

Sol. Given complex function will be analytic in nature if the real and imaginary part of the complex function satisfy the Cauchy Riemann equation i.e.

6. A particle moves in the one – dimensional potential where > 0 is a constant. If the total energy of the particle is E, its time period in a periodic motion is proportional to

(a) E^–1/3

(b) E^–1/2

(c) E^1/3

(d) E^1/2

Ans. (a)

Sol. For V(x) = αxⁿ

Its time period,

For n = 6,

7. Which of the following figures best describes the trajectroy of a particle moving on a repulsive central potential V (r) = a / r (a > 0 is a constant)?

(a)

(b)

(c)

(d)

Ans. (c)

Sol. Since, the given central potential is repulsive i.e., , the trajctory will be unbouned and paticle will be deflected away from the centre of force.

The graph given in option (c) best describes the trajectory

8. Two particles A and B move with relativistic velocities of equal magnitude v, but in opposite directions, along the x – axis of an inertial frame of reference. The magnitude of the velocity of A, as seen from the rest frame of B, is

(a)

(b)

(c)

(d)

Ans. (b)

Sol.

The velocity of A w.r.t. B's rest frame

Now, u = v, v = – v

Now, u = v, v = – v

9. A particle of mass m, kept in a potential (where k and are positive constants), undergoes small oscillations about an equilibrium point. The frequency of oscillations is

(a)

(b)

(c)

(d)

Ans. (c)

Sol.

For equilibrium points.

10. Tow point charges + 2Q and – Q are kept at points with Cartesian coordinates (1, 0 0) and (2, 0, 0), respectively, in front of an infinite grounded conducting plate at x = 0. The potential at (x, 0, 0) for x >> 1 depends on x as.

(a) x^–3

(b) x^–5

(c) x^–2

(d) x^–4

Ans. (d)

Sol.

Total charge Q = 2Q – Q + Q – 2Q = 0

The dipole moment of the system is

 

Coordinates of charges are

(x₁, y₁, z₁) = (2, 0, 0)

(x₂, y₂, z₂) = (1, 0, 0)

(x₃, y₃, z₃) = (–1, 0, 0)

(x₄, y₄, z₄) = (–2, 0, 0)

The quadropole moment of the charge distribution

Similarly,

T₁₂ = T₁₃ = ........... T₃₃ = 0

Therefore, quadropole moment of the charge distribution will be zero

Hence, potential will be due to octapole.

11. The following configuration of three identical narrow slits are illuminated by monochromatic light of wavelength (as shown in the figure below). The intensity is measured at an angle (where is the angle with the incident beam) at a large distance from the slits. If the intensity is proportional to

(a)

(b)

(c)

(d)

Ans. (c)

Sol.

12. The electric field of a plane wave in a conducting medium is given by where is the angular frequency and a > 0 is a constant. The phase difference between the magnetic field and the electric field is

(a)

(b)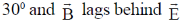

(c)

(d)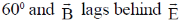

Ans. (b)

Sol.

Therefore, the phase between B and E is

B will lags behind to E by an angle = 30°

13. The electric field and the magnetic field 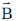corresponding to the scalar and vector potentials, V (x, y, z, t) = 0 and where A₀ is a constant, are

(a)

(b)

(c)

(d)

Ans. (b)

Sol. V(x, y, z, t) = 0

14. A particle of mass m is confined in a three – dimensional box by the potential

The number of eigenstates of Hamiltonian with energy is

(a) 1

(b) 6

(c) 3

(d) 4

Ans. (c)

Sol. Energy eigenvalues of a particle of mass m, confined in a 3-D box of size a is

The possible combinations of (n_x, n_y, n_z) are (2, 2, 1), (2, 1, 2), (1, 2, 2)

Therefore, the number of Eigen state of Hamiltonian with energy is 3.

15. The Hamiltonian of a spin particle in magnetic field is given by where is a real constant and are the Pauli spin matrices. If an the spin state at time t = 0 is an eigenstate of then of the expectation values

(a)

(b)

(c)

(d) All three change with time

Ans. (c)

Sol. Given Hamiltanian,

Now, the derivative of expectation values of any physical observable is given by

16. Two stern – Gerlach apparatus S₁ and S₂ are kept in a line (x – axis). The directions of their magnetic fields are along the positive z – and y – axes, respectively, Each appparatus only transmits particles with spins aligned in the direction of its magnetic field. If an initially unpolarized beam of spin particles passes through this configuration, the ratio of intensities I₀:I_f of the initial and final beam s, is

(a) 16 : 1

(b) 2 : 1

(c) 4 : 1

(d) 1 : 0

Ans. (c)

Sol.

Intensity of initial unpolarized beam of spi-½ particles = I₀

First Sterm Gerlach apparatus (having magnetic field along +ve z-axis) only transmit particles with spin aligned along +ve z-axis. So, after pssing thorugh the first sterm-Gerlach appratus, particles will be in Spin-up state of z-component of spin angular momentum and the intensity of the beam will be I₀/2.

Second Sterm-Gerlach appratus (having magnetic field along +ve y-axis) only transmit particles with spin aligned along +ve y-axis. So, after passing through the second Stern-Gerlach appratus, particles, will be in spin-up state of y-component of spin angular momentum and the intensity of the beam will be (½ factor occurs because the particles are in the spin-up state of S_z at incidence and probability of finding the paticles in the spin-up of S_y at emerges is 1/2).

17. A particle of mass m is constrained to move in a circular ring of radius R. when a perturbation (where a is a real constant) is added, the shift in energy of the ground state, to first order in a, is

(a) a / R²

(b) 2a / R²

(c) a / (2R²)

(d)

Ans. (c)

Sol.

The eigen state is

18. Which of the following statements concerning the coefficient of volume expansion and the isothermal compressibility k of a solid is true?

(a) and k are both intensive variables

(b) is an intensive and k is an extensive variable

(c) is an extensive and k is an intensive variable

(d) and k are both extensive variables

Ans. (a)

Sol. Since and k are the physical properties of the system that does not depend on the quantity of the material of the solid, they both must be intensive variable.

19. The van der Waals equation for one mole of a gas is . The corresponding equation of state for n moles of this gas at pressure p, volume V and temperature T is

(a)

(b)

(c)

(d)

Ans. (a)

Sol. The vander Waals equation for one moe of the gas is

where, V must be the molar volume of the gas.

To find the Vander waals equation for n moles of the gas, repalce V by . So, we have the required equation as .

20. The number of ways of distributing 11 indistinguishable bosons in 3 different energy levels is

(a) 3¹¹

(b) 11³

(c)

(d)

Ans. (c)

Sol. The required number of ways are

21. In a system of N distinguishable particles, each particle can be in one of two states with energies 0 and – E, respectively. The mean energy of the system at temperature T is

(a)

(b)

(c)

(d)

Ans. (d)

Sol. The partition function of one particle is

Z₁ = e^–0/kBT + e^E/kBT= 1 + e^E/kBT

Therefore, the partition function of N distinghishable particles is

Z_n = (Z₁)^N = (1 + e^E/kBT)^N

Therefore, the mean energy of the system is

22. In the following JK flip-flop circuit, J and K inputs are ties together to + V_CC. If the input is a clock signal of frequency f, the frequency of the output Q is.

(a) f

(b) 2f

(c) 3f

(d) f/2

Ans. (d)

Sol. J = K = 1 (Complement condition)

J = K = V_CC

23. Which of the following gates can be used as a parity checker?

(a) An OR gate

(b) a NOR gate

(c) an exclusive OR (XOR) gate

(d) an AND gate

Ans. (c)

Sol.

Output high for odd number 1's at input or even number of "0"s at input.

Parity either even or odd.

Therefore, XOR

24. A sinusoidal signal with a peak voltage V_p and average value zero, is an input to the following circuit.

Assuming ideal diodes, the peak value of the output voltage across the load resistor R_L, is

(a) V_p

(b) V_p / 2

(c) V_p

(d)

Ans. (c)

Sol.

Note : We can also solve this circuit using steps of clamping circuit.

: Value of capacitor is not going to affect analysis.

25. In the following circuit, the value of the common – emitter forward current implication factor for the transistor is 100 and V_BE is 0.1 V.

The base current I_B is

(a) 40 µA

(b) 30 µA

(c) 44 µA

(d) 33 µA

Ans. (d)

Sol.

26. In the function of real variable x, P_n(x) is a polynomial of degree n the maximum number of that this function can have is

(a) n + 2

(b) n – 1

(c) n + 1

(d) n

Ans. (c)

Sol.

x = 0, 1 extrema

Thus in general there are (n + 1) extrema.

27. The Green's function for the equation with the boundary values is

(a)

(b)

(c)

(d)

Ans. (b)

Sol.

28. The fractional error in estimating the integral using Simpson's rule, using a step size 0.1, is nearest to

(a) 10^–4

(b) 0

(c) 10^–2

(d) 3×10^–4

Ans. (b)

Sol.

29. Which of the following statements is true for a 3 × 3 real orthogonal matrix with determinant + 1?

(a) The modulus of each of its eigenvalues need not be 1, but their product must be 1

(b) At least one of its eigenvalues is + 1

(c) All of its eigenvalues must be real

(d) None of its eigenvalues need be real

Ans. (b)

Sol. The characteristic equation of any 3×3 matrix is of thee form which implies that at least one of the eigenvalues must be real. It is a proven fact that modulus of each eigenvalues of an orthogonal matrix is 1.

If all eigenvalues of 3×3 orthogonal matrix are real then only possibilities for eigenvalues are

Thus we see that at least one eigenvalue is +1. Suppose one eigenvalues is real and other two eigenvalues are complex conjugates. Now

Since a² + b² is always positive hence = 1.

In this case also we see that at least one eigenvalue must be +1.

30. A particle of mass m moves in a central potential in an elliptic orbit where and a and denote the semi – major axis and eccentricity, respectively. If its total energy is the maximum kinetic energy is

(a) E(1 – e²)

(b)

(c) E/(1 – e²)

(d)

Ans. (b)

Sol. The given potential energy is same as that of gravitational potential energy.

For elliptic orbit,

Maximum kinetic energy

31. The Hamiltonian of a one – dimensional system is where m and k are positive constants. The corresponding Euler – Lagrange equation for the system is

(a)

(b)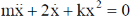

(c)

(d)

Ans. (c)

Sol.

We know that

Eq. (1), (2) put in Eq. (3)

Eq. (2) put in Eq. (4)

The Euler-Lagrange equation,

32. An inertial frame k´ moves with a constant speed v with respect to another inertial frame K along their common x – axis in the positive x – direction. Let (x, ct) and (x´,ct´) denote the space – time corrdinates in the frames K and K´, respectively. Which of the following space – time diagrams correctly describes the d´– axis (x´ = 0 line) and the x´–axis (t ´= 0 line) in the x – ct plane? (In the following figures tan – v / c.)

(a)

(b)

(c)

(d)

Ans. (b)

Sol. Minkowski space-time diagram for frames K and K'

33. The loop shown in the figure below carries a steady current I.

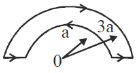
The magnitude of the magnetic field at the point 0 is

(a)

(b)

(c)

(d)

Ans. (b)

Sol. The resultant magnetic field at the centre is

34. In the region far from a source, the time dependent electric field at a point is

(a)

(b)

(c)

(d)

Ans. (b)

Sol. We have electric field,

So, the magnetic field

At far distance the first term will be negligible

Therefore, the pyonting vector,

Therefore, the total power radiated is

35. A hollow waveguide supports transverse electric (TE) modes with the dispersion relation where is the mode frequency. The speed of flow of electromagnetic energy at the mode frequency is

(a) c

(b)

(c) 0

(d)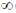

Ans. (c)

Sol.

36. The energy of a free relativistic particle is where m is its rest mass, is its momentum and c is the speed of light in vaccum. The ratio v_g / v_p of the group velocity v_g of a quantum mechanical wave packed (describing this particle) to the phase velocity v_p is

(a)

(b)

(c)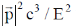

(d)

Ans. (c)

Sol.

37. The n – th energy eigenvalue E_n of a one – dimensional Hamiltonian (where > 0 is a constant) in the WKB approximation to

(a)

(b)

(c)

(d)

Ans. (a)

Sol. According to WKB approximation, if the potentail under which the particle is moving, is of the form V(x) = , then energy eigenvalues of the particle will be

38. The differential scattering cross – section for the central potential where and µ are positive constants, is calculated is the first Born approximation. Its dependence on the scattering angle 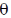is proportional to

(A is a constant below)

(a)

(b)

(c)

(d)

Ans. (c)

Sol. According to First Born approximation, scattering amplitude f() for a spherically symmatric potential V(r) will be

Therefore, differential cross-section will be

39. At t = 0, the wavefunction of another – wise free particle confined between two infinite walls at x = 0 and x = L is Its wave function at a later time is

(a)

(b)

(c)

(d)

Ans. (d)

Sol.

40. The pressure P of a system of N particles contained in a volume V at a temperature T is given by where n is the number density and a and b are temperature independent constants. It the system exhibits a gas – liquid transition, the critical temperature is

(a)

(b)

(c)

(d)

Ans. (c)

Sol. The given equation is

For critical temperature T_c, we have

This gives,

Dividing equation (2) by (3), we have

Putting this in equation (2), we have

41. Consider a particle diffusing in a liquid contained in a large box. The diffusion constant of the particle in the liquid is 1.0 × 10^–2 cm²/s. the minimum time after which the root – mean – squared displacement becomes more than 6 cm is

(a) 10 min

(b) 6 min

(c) 30 min

(d)

Ans. (a)

Sol. The root mean-squared displacement is

42. A thermally insulated chamber of dimensions (L, L, 2L) is partitioned in the middle. One side of the chamber is filled with n moles of an ideal gas at a pressure P and temperature T, while the other side is empty. At t = 0. The partition is removed and the gas is allowed to expand freely. The time to reach equilibrium varies as

(a) n^1/3L^–1T^1/2

(b) n^2/3LT^–1/2

(c) n⁰LT^–1/2

(d) nL^–1T^1/2

Ans. (c)

Sol. Correct option is (c)

43. The mamimum intensity of solar radiation is at the wavelength of and corresponds to its surface temperature T_sun ~ 10⁴ K. if the wavelength of a maximum intensity of an X – ray star in 5Å, its surface temperature is of the order of

(a) 10¹⁶K

(b) 10¹⁴ K

(c) 10¹⁰K

(d) 10⁷K

Ans. (d)

Sol. According to Wien's displacement law,

T = constant

where is the wavelength at which intensity of the solar radiation to a maximum an T is the temperature of the surface of the sun.

44. The full scale of a 3 – bit digital – to – analog (DAC) converter is 7 V. which of the following tables represents the output voltage of this 3 – bit DAC for the given set of input bits?

(a)

(b)

(c)

(d)

Ans. (a)

Sol. Full scale output of 3 bit DAC is 7 V.

For linear increased in digital input output analog must increase linearly.

Note : " –sign" will generate 180° phase shift.

Step-size = 1V.

Therefore, n = 3 bits.

45. The input V_i to the following circuit is a square wave as shown in the following figure.

Which of the waveforms V₀ best describes the output?

(a)

(b)

(c)

(d)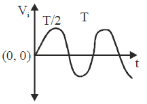

Ans. (b)

Sol. Given op-amp is differenciator.

Note : "–sign" will grenerate 180° phase shift.

Derivative of discontinuous function generate Dirac-delta function.

46. Two signals A₁ sin and A₂ cos are fed into the input and the reference channels, respectively, of a lock – in amplifier. The amplitude of each signal is 1 V. the time constant of the lock – in amplifier is such that is filtered out. The output of the lock – in amplifier is

(a) 2V

(b) 1V

(c) 0.5V

(d) 0V

Ans. (d)

Sol.

A₁ and A₂ each 1 volt.

Hence, 0 volte output.

47. A photon of energy 115.62 keV ionizes a K – sheel electron of a Be atom. One L – shell electron jumps to the K – shell to fill this vacancy and emits a photon of energy 109.2 keV in the process. F the ionization potential for the L – shell is 64. keV, the kinetic energy of the ionized electron is

(a) 6.42 keV

(b) 12.82 keV

(c) 20 eV

(d) 32 eV

Ans. (c)

Sol. Given: e_L – E_k = 109.2 KeV and ionization potential for L-shell = 6.4 KeV

Ionization potential for K-shell i.e. for sending electron from n = 1 to n =

= 109.2 + 6.4 = 115.6 KeV

But 115.62 KeV energy is given to the k-shell electron of Be atom. The extra energy will be equal to kinetic energy and is given by

K.E. = 115.62 – 115.6 = 0.02 KeV = 20 eV

48. The value of the Lande g – factor for a fine – structure level defined by the quantum numbers L = 1, J = 2 and S = 2, is

(a) 11/6

(b) 4/3

(c) 8/3

(d) 3/2

Ans. (d)

Sol. The value of Lande g-factor

49. The electronic energy level diagram of a molecule is shown in following figure.

Let denote the decay rate for a transition from the level i to j. the molecules are optically pumped from level 1 to 2. For the transition from level 3 to level 4 to be a lasing transition, the decay rates have to satisfy.

(a)

(b)

(c)

(d)

Ans. (c)

Sol. Decay rate is inversely propotional to life time of upper level of transition.

For laser action, population iversion is maintained between levels 3 and 4. For which

(i) Transition form 2 to 1 should be almost negligible or we can say time of transition T₂₁ is large.

(ii) Transition from 2 to 3 should be fast (fast decay) i.e. T₂₃ 0 (or very small)

(iii) For population inversion, level 4 should empty fast i.e. it is normal energy level i.e. T₄₁(= 10^–8 sec)

Thus, T₄₁ > T₂₃ < T₂₁ < T₃₄. Thus for decay rates.

50. Sodium chloride (NaCl) crystal is a face centred cubic lattice, with a basic consisting of Na⁺ and Cl^– ions separated by half the body diagonal of a unit cube. Which of the planes corresponding to the miller indices given below will not give rise to Bragg reflectionof X – ray?

(a) (2 2 0)

(b) (2 4 2)

(c) ( 2 2 1)

(d) (3 1 1)

Ans. (c)

Sol. The coordination

then the diffraction amplitude is

and structure factor is

Here in fcc the structure factor is non-zero if h, k l are all even or odd.

So, in option (c there is the combination even and odd. So, (2 2 1) are not reflection of the fcc.

51. The dispersion relation for the electrons in the conduction band of a semiconductor is given by E = E₀ + ak², where and E₀ are constants. If is the cyclotron resonance frequency of the conduction band electrons in a magnetic field B, the value of is

(a)

(b)

(c)

(d)

Ans. (d)

Sol. The cyclotron frequency of the conduction band electron in a magnetic field is

m = effective mass of electron

52. Hard discs of radius R are arranged in two – dimensional triangular lattice. What is the fractional area occupied by the discs in the closest possible packing?

(a)

(b)

(c)

(d)

Ans. (a)

Sol.

53. Which of the following elementary particle processes does not conserve strangeness?

(a)

(b)

(c)

(d)

Ans. (d)

Sol.

i.e. strangeness is not conserved.

54. A deuteron d captures a charged point in the l = 1 state, and subsequently decays into a pair of neutrons (n) via strong interaction. Given that the intrinsic parties of , d and n are – 1, + 1 and + 1 respectively, the spin – wavefunction of the final state neutrons is a

(a) Linear combination of a singlet and a triplet

(b) Singlet

(c) Triplet

(d) Doublet

Ans. (b)

Sol. The capture of a charged pion (in the = l state) by the deuteron,

In this case capture takes place in = 1 state. So, the spatial parity of the initial state is odd. Also, the parity of the deuteron ground state is even. So, the total parity of the intial state is determined by the parity of .

Since, , the total angular momentum of the intial state is

In the final state (n + n) the following state are permissible by Pauli principle.

Singlet states: ¹S₀, ¹D₂, ¹G₄ with = 0, 2, 4, etc.

Triplet states: ³P₀₁₂, ³F₂₃₄, ³H₄₅₆ etc with L = 1, 3, 5 etc.s

For the first group, the spin wave function are odd, while the spatial wave function are even, so, that the total wave function is odd, as is requried by Pauli principle, because the neutrons are fermions. For the second group, the spin functions are even, while the spatial function are odd, again making the total wave function odd.

To conserve the total angular momentum, the final state must be ¹S₀ or ¹D₂ or mixture of ¹S₀ and ¹D₂ which means L = 0 or L = 2 for the final state, giving the spatial parity even. Since, the neutrons have even intrinsic parity, the total parity of the final state must be even. Since, for strong interaction parity must be conserved.

The partity of initial state (–1)^λ (–1) = (–1)¹ (–1) = + 1 (even)

55. The reaction is followed by a prompt – decay of zinc If the maximum energy of the positron is 2.4 meV, the Q – value of the original reaction in meV is nearest to

[Take the masses of electron proton and neutron to be 0.5 MeV/c², 938 MeV/c² and 939.5 MeV/c², respectively.]

(a) – 4.4

(b) – 2.4

(c) – 4.8

(d) – 3.4

Ans. (a)

Sol. Since the maximum energy of positron is 2.4 meV, therefore the Q-value of the -deacy of Zinc is 2.4 MeV.

Thus, for -decay reaction:

Now, for original recation, ⁶³Cu₂₉ + p ⁶³Zn₃₀ + n

The Q-value is given by

Q = (M_nuc. (Cu⁶³) + m(p) – M_nuc.) (Zn⁶³) – m(n))c²

= [M_nuc. (Cu⁶³) – M_muc. (Zn⁶³ )] c² + [m(p) – m(n)]c²

+ [938 – 939.5] MeV = – 2.9 MeV – 1.5 MeV = – 4.4 MeV