1. Which of the following two physical quantities cannot be measured simultaneously with arbitrary accuracy for the motion of a quantum particle in three dimensions?

(a) square of the radial position and z-component and angular momentum (r² and L_z)

(b) x-components of linear and angular momenta (p_x and L_x)

(c) y-component of position and z-component of angular momentum (y and L_x)

(d) squares of the magnitudes of the linear and angular momenta (p² and L²)

Ans. (c)

Sol. The two physical quantities cannot be measured simultaneously with arbitrary accuracy in quantum mechanics whose commutator is not zero.

(a) [r², L_z] = [x² + y² + z², L_z]

= [x², L_z] + [y², L_z] + [z², L_z]

= x[x, L_z] + [x, L_z]x + y[y, L_z] + [y, L_z]y

=

where, we have used

(b) [p_x, L_x] = [p_x, yp_z, zp_y]

= [p_x, yp_z] – [p_x – zp_y]

= y[p_x, p_z] + [p_x, y]p_z + z[p_x, p_z] – [p_x, z]p_y

[p_x, L_x] = 0

where, we have used

[p_x, p_z] = [p_x, y] = [p_x, z] = 0

(c)

= 0

where, we have used

[p, r] = 0

(d) [y, L_z] = [y₁xp_y – yp_x]

= [y xp_y] – [y₁yp_x]

= x[y₁p_y] + [y₁x]p_y – y[y₁p_x] – [y₁y]p_x

= x[y₁p_y] + 0 + 0 + 0 =

where we have used

2. A particle in one dimension executes oscillatory motion in a potential V(x) = A|x|, where A > 0 is a constant of appropriate dimension. If the time period T of its oscillation depends on the total energy E as E^a, then the value of a is

(a) 1/3

(b) 1/2

(c) 2/3

(d) 3/4

Ans. (b)

Sol. Total energy

Action angle variable

J = x₀E^3/2

Time period

3. The components of the electric field, in a region of space devoid of any change or current sources, are given to be E_i = a_i + b_ijx_j, where a_i and b_ij are constant independent of the coordinates. The number of independent components of the matrix b_ij is

(a) 5

(b) 6

(c) 3

(d) 4

Ans. (a)

Sol.

This equation represents a set of three equations

Let E₁ = E_x, E₂ = E_y, E₃ = E_z and x₁ = x, x₂ = y, x₃ = z, (1) can be written as

Let's just look at the x-component (which will be equal to zero).

Similarly, we will get from 'y' and 'z' components

b₁₃ = b₃₁, b₂₁ = b₁₂

Thus, it means b_ij is symmetric. a symmetric matrix will have, 3 diagonal +3 off diagonal = 6 – independent components – (4)

Also, as the region is charge free, therefore

Putting this result in (5), we get

b₁₁ + b₂₂ + b₃₃ = 0.

This implies that atleast one of the diagonal elements is dependent. Therefore, the total number of independent components = 6 – 1 = 5.

Therefore, (a) is correct option.

4. A particle of mass 1 GeV/c² and its antiparticle, both moving with the same speed v, produce new particle x of mass 10 GeV/c² in a head on collision. The minimum value of v required for this process is closest to

(a) 0.83c

(b) 0.93c

(c) 0.98c

(d) 0.88c

Ans. (c)

Sol.

Conservation of energy

5. The position of a particle in one dimension changes in discrete steps. With each step it moves to the right, however, the length of the step is drawn from a uniform distribution from the interval , where and w are positive constants. If X denotes the distance from the starting point after N steps, the standard deviation for large values of N is

(a)

(b)

(c)

(d)

Ans. (d)

Sol. Correct option is (d).

6. The volume of the region common to the interiors of two infinitely long cylinders defined by x² + y² = 25 and x² + 4z² = 25 is best approximated by

(a) 225

(b) 333

(c) 423

(d) 625

Ans. (b)

Sol.

In any of the above equations, 'x' varies from –5 to 5. Therefore, the volume bounded in the intersecting region is

7. The donor of an X-ray machine room is fitted with a sensor D (0 is open and 1 is closed). It is alos equipped with three fire sensors F₁, F₂ and F₃ (each is 0 when disabled and 1 when enabled). The X-ray machine can operate only if the door is closed and at least 2 fire sensors are enabled. The logic circuit to ensure that the machine can be operated is

(a)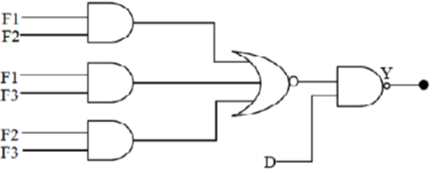

(b)

(c)

(d)

Ans. (a, b, d)

Sol.

8. In the LCR circuit shown below, the resistance R = , the inductance L = 1/H and the capacitance C = 0.04 F.

If the input v_in is a square wave of angular frequency 1 rad/s, the output v_out is best approximated by a

(a) Square wave of angular frequency 1 rad/s

(b) Sine wave of angular frequency 1 rad/s

(c) Square wave of angular frequency 5 rad/s

(d) Sine wave of angular frequency 5 rad/s

Ans. (d)

Sol. v_in = 1 rad/s, L = 1H, C = 0.04 F

Resonant angular frequency

Thus, for an input frequency of 1 rad/s (just like dc), the LC-circuit will oscillate in sinusoidal fashion (it can only oscillate harmonically), at 5 rad/s. Hence, (d) is the correct answer.

9. A monochromatic source emitting radiation with a certain frequency moves with a velocity v away from a stationary observer A. It is moving towards another observer B (also at rest) along a line joining the two. The frequencies of the radiation recorded by A and B are V_A and V_B, respectively. If the ratio , then the value of v/c is

(a) 1/2

(b) 1/4

(c) 3/4

(d)

Ans. (c)

Sol.

10. A particle, thrown with a speed v from the earth's surface, attains a maximum height h (measured from the surface of the earth). If v is half the escape velocity and R denotes the radius of earth, then h/R is

(a) 2/3

(b) 1/3

(c) 1/4

(d) 1/2

Ans. (b)

Sol.

Here M is the mass of the earth.

Conservation of mechanical energy

3R + 3h = 4R

3h = R

11. A particle of mass m is in a one dimensional infinite potential well of length L, extending from x = 0 to x = L. When it is in the energy Eigen-state labelled by n, (n = 1, 2, 3, ...) the probability of finding in the interval 0 < x < L/8 is 1/8. The minium value of n for which this is possible is

(a) 4

(b) 2

(c) 6

(d) 8

Ans. (a)

Sol. This problem is solved using the wavefunction

(a) The plot for between 0 < x < L is

The probability of finding the particle in region 0 < x < L/2 and L/2 < x < L is

(b) The plot for between 0 < x < L

The probability of finding the particle in region

(c) The plot for in region 0 < x < L is

The plot is divided in 6 equal region of

The probability of finding the particle in each of region is 1/6.

(d) The plot for between 0 < x < L is

The wave function is divided in 8 equal region of

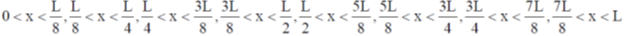
The probability of finding the particle in each of these region is 1/8.

Thus, the value of n = 4, such that the probability of finding the particle in region .

12. In an experiment, the velocity of a non-relativistic neutron is determined by measuring the time (~ 50 ns) it takes to travel from the source to the detector kept at a distance L. Assume that the error in the measurement of L is negligibly small. If we want to estimate the kinetic energy T of the neutron to within 5% accuracy, i.e., < 0.05, the maximum permissible error in measuring the time of flight is nearest to

(a) 1.75ns

(b) 0.75ns

(c) 2.25 ns

(d) 1.25ns

Ans. (d)

Sol. The correct option is (d).

13. The volume and temperature of a spherical cavity filled with black body radiation are V and 300K, respectively. If it expands adiabatically to a volume 2V, its temperature will be closest to

(a) 150 K

(b) 300 K

(c) 250 K

(d) 240 K

Ans. (d)

Sol. V₁ = V, T₁ = 300 K

V₂ = 2V, T₂ = ?

VT³ = constant

14. The ratio c_p/c_v of the specific heats at constant pressure and volume of a monatomic ideal gas in two dimensions is

(a) 3/2

(b) 2

(c) 5/3

(d) 5/2

Ans. (b)

Sol. For monoatomic ideal gas in 2D

U = NKT = nN_AkT = nRT

15. The total number of phonon modes in a solid of volume V is 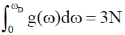, is the number of primitive cells, is the Debye frequency and density of photon modes is g(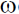) = AV² (with A > 0 a constant). If the density of the solid doubles in a phase transition, the Debey temperature will

(a) increase by a factor of 2^2/3

(b) increase by a factor of 2^1/3

(c) decrease by a factor of 2^2/3

(d) decrease by a factor of 2^1/3

Ans. (b)

Sol. Deby temperature is

Thus Q_D increases by a factor of 2^1/3.

16. A discrete random variable X takes a value from the set {–1, 0, 1, 2} with the corresponding probabilities p(X) = 3/10, 2/10, 2/10 and 3/10, respectively. The probability distribution q(Y) = [q(0), q(1), q(4)] of the random variable Y = X² is

(a)

(b)

(c)

(d)

Ans. (b)

Sol. Given that,

X = {–1, 0, 1, 2};

X² = {0, 1, 4}; p(X²) = {––, ––, – – –} = ?

For

For,

For (X = –2 is not in the list),

Hence, (b) is correct option.

17. In an experiment to measure the charge to mass ratio e/m of the electron by Thomson's method, the values of the deflecting electric field and the accelerating potential are 6 × 10⁶ N/C (newton per coulomb) and 150V, respectively. The magnitude of the magnetic field that leads to zero deflection of the electron beam is closest to

(a) 0.6 T

(b) 1.2 T

(c) 0.4 T

(d) 0.8 T

Ans. (d)

Sol. Let's determine the velocity of an electron accelerated to 150 V.

Using, the classical formula relating kinetic energy and accelerating potential, mv² = eV

For zero deflection,

Thus, (d) is the correct option.

18. A two state system evolves under the action of the Hamiltonian H = where, and are its two orthonormal states. These states transform to one another under parity, i.e. P and P. If at time t = 0 the system is in a state of definited parity P =1, the earliest time t at which the probability of finding the system in a state of parity P = –1 is one is

(a)

(b)

(c)

(d)

Ans. (b)

Sol. The Hamiltonian for the two state system is given by

In matrix,

The energy eigenvalue for the system is given by

The eigenfunction of the system is given by

According to question, we have

Comparing coefficent of state and , we get

Since both these conditions are same, we

Thus, the correct option is (b).

19. A conducting wire in the shape of a circle lies on the (x, y) plane with its centre at the origin. A bar magnet moves with a constant velocity towards the wire along the z-axis (as shown in the figure below)

We take t = 0 to be the instant at which the midpoint of the magnet is at the centre of the wire loop and the induced current to be positive when it is counter-clockwise as viewed by the observer facing the loop and the incoming magnet. In these conventions, the best schematic representation of the induced current I(t) as a function of t, is

(a)

(b)

(c)

(d)

Ans. (d)

Sol. As, north pole of the magnet moves towards the coil, the induced current must flow in a direction (clockwise as seen from right) to create north polarity on left. However, the current seen from right and flowing counterclockwise is to be considered positive. This

current will produce a south polarity on the left of the coil. Thus, as seen by an observer from right, the current must flow clockwise to produce a north polarity on left. This clockwise current will be negative. Thus, as the bar magnet approaches the coil, first induced current will be negative and after it is about to cross, induced current must be positive. Thus, option (d) should be the correct answer.

20. The vector potential for an almost point like magnetic dipole located at the origin is where denote the spherical polar coordinates and is the unit vector along . A particle of mass m and charge q, moving in the equatorial plane of the dipole, starts at time = t = 0 with an initial speed v₀ and an impact parameter b. Its instantaneous speed at the point of closest approach is

(a) v₀

(b) 0/0

(c)

(d)

Ans. (a)

Sol. A static magnetic field does not alter the magnitude of speed of a charged particle. It only alters the direction of motion. Hence, its speed will be the same as the one it started with. (i.e., v₀). Thus, (a) is the correct answer.

21. The equation of motion of a one-dimensional forced harmonic oscialltor in the presence of a dissipative force is described by + + 16x = 6te^–8t + 4t²e^–2t. The general form of the particular solution, in terms of constants A, B etc., is

(a) t(At² + Bt + C)e^–2t + (Dt + E)e^–8t

(b) (At² + Bt + C)e^–2t + (Dt + E)e^–8t

(c) t(At² + Bt + C)e^–2t + t(Dt + E)e^–8t

(d) (At² + Bt + C)e^–2t + t(Dt + E)e^–8t

Ans. (c)

Sol. Given differential equation + + 16x = 6te^–8t + 4t²e^–2t

Thus, the complementary function can be written as

y_cf = ae^–8t + be^–2t ...(1)

The last terms in the above expression can be coupled with complementary function

Therefore, A' = t[Dt + E]e^–8t ...(3)

The last terms in the above expression can be coupled with complementary function

Therefore, B' = t[At² + BT + C]e^–2t ...(4)

From (3) and (4)

PI = t[At² + BT + C]e^–2t + t[Dt + E]e^–8t ...(5)

Thus, (c) is correct option.

22. The figures below depict three different wave functions of a particle confined to a one dimensional box –1 < x < 1

The wave function that correspond to the maximum expectation values (absolute value of the mean position) and 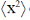, respectively are

(a) B and C

(b) B and A

(c) C and B

(d) A and B

Ans. (a)

Sol. This problem is solved using properties :

(1) For a box of length –a < x < d, is always zero.

(2) For a 60x of length –a < x < d, is always non zero.

(3) The wavelength is of the form

= A(a² – x²)

The normalised wave function is given by

The expectation value of 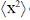is

Thus, a a = +1 curve would take maximum and minimum values.

For the curve given in the option (b) is non-zero.

For , the curve takes maximum and minimum value at a = +1 in the curve shown in option (c).

23. The Hamiltonian of a particle of mass m in one-dimension is H = p² + |x|³, where > 0 is a constant. If E₁ and E₂ respectively, denote the ground state energies of the particle for = 1 and = 2 (in appropriate units) the ratio E₂/E₁ is best approximated by

(a) 1.260

(b) 1.414

(c) 1.516

(d) 1.320

Ans. (d)

Sol. Consider the potential of the particle of form

V(x) = |x|ⁿ

The ground state energy of the particle using with approximation depends on .

24. A generic 3 × 3 real matrix A has eigenvalues 0, 1 and 6 and I is the 3 × 3 identity matrix. The quantity/quantities that cannot be determined from this information is/are the

(a) eigenvalue of (I + A)^–1

(b) eigenvalue of (I + A^TA)

(c) determinant of A^TA

(d) rank of A

Ans. (b)

Sol. Given Eigen values are = 0, 1, 6

Eigen values of I + A are = 1 + Eigen values of A

Therefore, Eigen values of (I + A)^–1 are = 1,

Therefore, 'a' can be determined

|A| = 0 × 1× 6 = 0, |A^T| = 0 × 1 × 6 = 0

Therefore, |AA^T| = |A||A^T| = 0

Thus, (c) can also be determined.

As one Eigen value is 0. Therefore, rank is 3 – 1 = 2. Hence, 'd' can also be determined.

Thus, 'b' cannot be determined. Hence, it is the correct answer.

25. The volume integral I = , is over a region V bounded by a surface (an infinitesimal area element being ds, where is the outward unit normal). If it changes to I + when the vector is changed to then can be expressed as

(a)

(b)

(c)

(d)

Ans. (c)

Sol.

Now, the curl of the gradient always vanishes

Therefore, the above equation becomes.

The first term in the above expression is just the I. Thus, we get

The second term vanishes again. Therefore, we get

Substituting, this result in (A), we get

Using, divergence theorem, we get

Thus, (c) is the correct option.

26. The Newton-Raphson method is to be used to determine the reciprocal of the number x = 4. If we start with the initial guess 0.20 then after the first iteration the reciprocal is

(a) 0.23

(b) 0.24

(c) 0.25

(d) 0.26

Ans. (b)

Sol. To find the inverse of 4, let

Thus, we need the solution of this equation after first iteration.

Starting point, x₀ = 0.20

Hence, (b) is correct option.

27. A laser beam propagates from fiber 1 to fiber 2 in a cavity made up of two optical fibres (as shown in the figure). The loss factor of fiber 2 is 10 dB/km.

If E₂(d) denotes the magnitude of the electric field in fiber 2 at a distance d from the interface, the ratio E₂(0)/E₂(d) for d = 10 km, is

(a) 10²

(b) 10³

(c) 10⁵

(d) 10⁷

Ans. (c)

Sol. The correct option is (c).

28. The fulcrum of a simple pendulum (consisting of a particle of mass m attached to the support by a massless string of length l) oscillates vertically as sin z (t) = a sine t, where is a constant. The pendulum moves in a vertical plane and 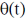denotes its angular position with respect to the z-axis.

If (where g is the acceleration due to gravity) describes the equation of motion of the mass, then f(t) is

(a)

(b)

(c)

(d)

Ans. (d)

Sol. The generalised coordinate is (lsinθ, –lcosθ + z)

Lagrangian is given by

In problem it is given by

29. The energies of a two-state quantum system are E₀ and E₀ + , (where > 0 is a constant) and the corresponding normalized state vectors are respective. At time t = 0, when the system is in the state . the potential is altered by a time independent term V such that The transition probability to the state at times t 1/, is

(a)

(b)

(c)

(d)

Ans. (c)

Sol. The transmission probability to the state 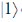at time t is

30. The nuclei of ¹³⁷Cs decay by the emission of -particles with a half-life of 30.08 years. The activity (in units of disintegrations per second or Bq) of a 1 mg source of ¹³⁷Cs, prepared on January 1, 1980, as measured on January 1, 2021 is closest to

(a) 1.79 × 10¹⁶

(b) 1.79 × 10⁹

(c) 1.24 × 10¹⁶

(d) 1.24 × 10⁹

Ans. (d)

Sol.

= 0.023 × 4.3 × 10¹⁸ × e^–0.922 (Disintegration per year)

= 0.023 × 4.3 × × 10¹⁸ × 0.3977

= 0.0393 × 10¹⁸ (Disintegration per year)

=

= 1.24 × 10⁹ (dps)

31. To measure the height h of a column of liquid helium in a container, a constant current I is sent through an NbTi wire of length l , as shown in the figure. The normal state resistance of the NbTi wire is.

If the superconducting transition temperature of NbTi is 10K, then the measured voltage V (h) is best described by the expression

(a)

(b)

(c)

(d)

Ans. (d)

Sol. Since the superconducting critical temperature for NOT is 30K, the partition of the wire immersed in the liquid Helium is in the superconducting state with zero resistance, while the partition above the liquid is in normal state with resistance R.

where

The resistance of the wire of length l is

Since,

V = 1R'

Thus correct answer is (d).

32. Diffuse hydrogen gas within a galaxy may be assumed to follow a Maxwell distribution at temperature 10⁶ K, while the temperature appropriate for the H gas in the inter-galactic space, following the same distribution, may be taken to be 10⁴ K. The ratio of thermal broadening of the Lyman-α line from the H-atoms within the galaxy to that from the inter-galactic space is closest to

(a) 100

(b) 1/100

(c) 10

(d) 1/10

Ans. (c)

Sol. The correct option is (c).

33. The dispersion relation of a gas of non-interacting bosons in d dimensions E(k) = ak^s where a and s are positive constants, Bose-Einstein condensation will occur for all values of

(a) d > s

(b) d + 2 > s > d – 2

(c) s > 2 independent of d

(d) d > 2 independent of s

Ans. (a)

Sol. Given the dispersion relation

E(k) = ak^s ...(1)

For a non-relative system in 3-D

In 2-D relativistic

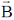34. A perfectly conducting fluid of permittivity and permeability µ flows with a uniform velocity in the presence of time dependent electric and magnetic fields and , respectively, if there is a finite current density in the fluid, then

(a)

(b)

(c)

(d)

Ans. (a)

Sol. The generalised Ohm's law for conducting fluids is given by

If, there is no net current, = 0. Thus, the above equation becomes,

being common, cancel's out.

Taking curl of the above equation, we get

Thus, (a) is the correct answer.

35. The pressure of a gas in a vessel needs be maintained between 1.5 bar to 2.5 bar in an experiment. The vessel is fitted with a pressure transducer that generates 4 mA to 20 mA current for pressure in the range 1 bar to 5 bar. The current output of the transducer has a linear dependence on the pressure.

The reference voltage V₁ and V₂ in the comparators in the circuit (shown in figure above) suitable for the desired operating conditions are respectively

(a) 2V and 10V

(b) 2V and 5V

(c) 3V and 10V

(d) 3V and 5V

Ans. (d)

Sol. 4 mA to 20 mA current for pressure in the range 1 bar to 5 bar.

So 1 bar corresponds to 4 mA.

So 1.5 bar = 6 mA V₁ = 6 mA × 500 = 3.0 V

So 2.5 bar = 10 mA V₂ = 10 mA × 500 = 5.0 V

36. The energy levels of a non-degenerate quantum system are = nE₀, where E₀ is a constant and n = 1, 2, 3, ... . At a temperature T, the free energy F can be expressed in terms of the average energy E by

(a)

(b)

(c)

(d)

Ans. (c)

Sol.

Now Helmholtz free energy

From (2) and (3)

37. A particle in two dimensions is found to trace an orbit r() = r₀². If it is moving under the influence of a central potential V(r) = c₁r^–a + c₂r^–b, where r₀, c₁ and c₂ are constants of appropriate dimensions, the values of a and b, respectively are

(a) 2 and 4

(b) 2 and 3

(c) 3 and 4

(d) 1 and 3

Ans. (b)

Sol.

Differential equation of the orbit

f(r) = – Ar^–4 – Br^–3

where A and B are constants

V(r) = c₁r^–3 + c₂r^–2 = c₁r^–a + c₂r^–b

a = 3

b = 2

38. A particle of mas m moves in a potential that is V = in the coordinates of a non-inertial frame F. The frame F is rotating with respect to an inertial frame with an angular velocity , where it is the unit vector along their common z axis. The motion of the particles is unstable for all angular frequencies satisfying

(a)

(b)

(c)

(d)

Ans. (b)

Sol. The correct option is (b).

39. A ⁶⁰Co nucleus -decays from its ground state with J^P = 5⁺ to a state of ⁶⁰Ni with J^P = 4⁺. From the angular momentum selection rules, the allowed values of the orbital angular momentum L and the total spin S of the electron-antineutrino pair are

(a) L = 0 and S = 1

(b) L = 1 and S = 0

(c) L = 0 and S = 0

(d) L = 1 and S = 1

Ans. (a)

Sol.

So, the given transition is allowed Gamow-Teller transition. So allowed values of the orbital angular momentum L and the total spin S of the electron-antineutrino pair are

L = 0 and S = 1

40. A satellite of mass m orbits around earth in an elliptic trajectory of semi-major axis a. At a radial distance r = r₀, measured from the centre of the earth, the kinetic energy is equal to half the magnitude of the total energy. If M denotes the mass of the earth and the total energy is , the values of r₀/a is nearest to

(a) 1.33

(b) 1.48

(c) 1.25

(d) 1.67

Ans. (a)

Sol.

The potential energy at r = r₀ will be

From Eqs. (1) and (2)

41. A particle of mass m in one dimension is in the ground state of a simple harmonic oscillator described by a Hamiltonian H = in the standard notation. An impulsive force at time to t = 0 suddenly imparts a momentum p₀ = to it. The probability that the particle remains in the original ground state is

(a) e^–2

(b) e^–3/2

(c) e^–1

(d) e^–1/2

Ans. (d)

Sol. The new state of the system is

In an expansion in the complete set of harmonic oscillator eigen function.

the coefficient

are the probability amplitudes for the system in the state Thus

Calculating the Guarian integral

Substituting value in expression of probability.

We get

where, we have used

42. A polymer, made up of N monomers, is in thermal equilibrium at temperature T. Each monomer could be of length a or 2a. The first contributes zero energy, while the second one contributes . The average length (in units of Na) of the polymer at temperature T = /k_B is

(a)

(b)

(c)

(d)

Ans. (d)

Sol. When length of monomer is

a, energy = 0

2a, energy =

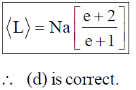
43. The figure below shows an ideal capacitor consisting of two parallel circular plates of radius R. Points P₁ and P₂ are at a transverse distance, r₁ > R from the line joining the centers of the plates, while points P₃ and P₄ are at a transverse distance r₂ < R.

It B(x) denotes the magnitude of the magnetic fields at these points, which of the following holds while the capacitor is charging?

(a) B(P₁) < B(P₂) and B(P₃) < B(P₄)

(b) B(P₁) > B(P₂) and B(P₃) > B(P₄)

(c) B(P₁) = B(P₂) and B(P₃) < B(P₄)

(d) B(P₁) = B(P₂) and B(P₃) > B(P₄)

Ans. (c)

Sol.

Magnetic field at P₂ and P₄ can be simply written using Ampere's law (as these points are outside the capacitor, therefore magnetic field only depends upon the magnitude of free current which is just I).

Thus, B₂(r) = and B₄(r) =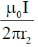

At P₁ and P₃, magnetic field depends upon displacement current.

Field at P₁ :

The conduction current is zero. Further, note that the displacement current does not flow outside the plates, therefore r = R on R.H.S and r = r₁ on L.H.S.

Thus, we get

Field at P₃ :

Note that displacement current flowing through only r = r₂ counts on R.H.S. Therefore, r = r₂ on R.H.S. as well as on L.H.S.

Thus, we get

Comparing, B₁ = B₂

and

Thus (c) is the correct answer.

44. The 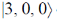state in the standard notation of the H-atom in the non-relativistic theory decays to the state via two dipole transition. The transition route and the corresponding probability are

(a)

(b)

(c)

(d)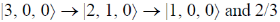

Ans. (c)

Sol. For dipole transition,

For all options, n = 2, so l = 0, 1

The transitions for m = –1, 0, 1 are all valid according to the dipole transition rule. Thus, there are three different states through which the state can decay to each with equal probability. Hence each transition has a probability of 1/3. So, option (c) with probability 1/3 is correct.

45. Balls of ten different colours labeled by a = 1, 2, ..., 10 are to be distributed among different coloured boxes. A ball can only go in a box of the same colour and each box can contain at most one ball. Let n_a and N_a denote respectively, the numbers of balls and boxes of colour a. Assuming that N_a >> n_a >> 1, the total entropy (in units of the Boltzmann constant) can be best approximated by

(a)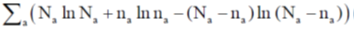

(b)

(c)

(d)

Ans. (b)

Sol. Let n₁ balls of colour 1 to be distributed in N₁ boxes of colour 1

n₂ balls of colour 2 to be distributed in N₂ boxes of colour 2

n₁₀ balls of colour 10 to be distributed in N₁₀ boxes of colour 10

46. A linear diatomic molecule consists of two identical small electric dipoles with an equilibrium separation R, which is assumed to be a constant. Each dipole had charges +q of mass m separated by r when the molecule is at equilibrium. Each dipole can execute simple harmonic motion of angular frequency

Recall that the interaction potential between two dipoles of moments and , separated by

Assume that R r and let . The angular frequencies of small oscillations of the diatomic molecule are

(a)

(b)

(c)

(d)

Ans. (c)

Sol. We need to remember that for two coupled oscillators (two equal masses attached by a spring of force constant and attached to the walls from two sides with a spring of force constant k), the difference of squares of allowed frequency of oscillations is given by

The situation here is identical. The interaction energy of two dipoles which are parallel is given by (given in the statement of the problem and taking the angle between the parallel dipoles to be zero degree)

Therefore, substituting the value of force constant obtained above in the (1), we get

The value of is given in the statement of the problem. This is the difference expected in the two frequencies. If we look for this difference of frequencies in the given options, only (c) satisfies this criterion. Therefore, it is the correct option.

47.

(a) 3/5

(b) 11/15

(c) 23/32

(d) 16/35

Ans. (d)

Sol. Let

4 + 2x – 3x² + 4x³ = a₀P₀(x) + a₁P₁(x) + a₂P₂(x) + a₃P₃(x)

Comparing, we get

Therefore,

Other integrals vanish because of orthogonal property. Thus, (d) is correct option.

48.

(a)

(b)

(c)

(d)

Ans. (c)

Sol.

Given equation

Multiplying both sides by e^–ikx and integrating with respect to 'x', we get

Using y = e^z, (2) becomes

The auxiliary equation can be written as

The solution of (3) can therefore be written as

Reverting to original variable, we get

Thus, (c) is correct option.

49. In the following circuit the input voltage V_in in such that |V_in| < |V_sat| where V_sat is the saturation voltage of the op-amp (Assume that the diode is an ideal one and R_LC is much larger than the duration of the measurement).

For the input voltage as shown in the figure above the output voltage V_out is best represented by

(a)

(b)

(c)

(d)

Ans. (a)

Sol. It's a peak detector circuit so options (a) is correct.

50. Potassium chloride forms an FCC lattice, in which K and Cl occupy alternating sites. The density of KCl is 1.98 g/cm³ and the atomic weights of K and Cl are 39.1 and 35.5, repsectively. The angles of incidence (in degrees) for which Bragg peaks will appear when X-ray of wavelength 0.4 nm is shone on a KCl crystal are

(a) 18.5, 39.4 and 72.2

(b) 19.5 and 41.9

(c) 12.5, 25.7, 40.5 and 6.0

(d) 13.5, 27.8, 44.5 and 69.0

Ans. (a)

Sol. Lattice Parameter is

a = 6.3 × 10^–8 cm = 6.3 A°

Bragg's law is

For (200) plane

Thus option (a) is correct.

51. Lead is superconducting below 7K and has a critical magnetic field 800 × 10^–4 tesla close to 0K. At 2K the critical current that flows through a long lead wire of radius 5 mm is closest to

(a) 1760 A

(b) 1670 Ac

(c) 1950 A

(d) 1840 A

Ans. (d)

Sol. Critical field at temperature T is

Given B_c(c) = 800 × 10^–4 T, T_c = 7k

Critical current is

52. The Q-value of the -decay of ²³²Th to the ground state of ²³⁸Ra in 4082 keV. The maximum possible kinetic energy of the -particles is closest to

(a) 4082 keV

(b) 4050 keV

(c) 4035 keV

(d) 4012 keV

Ans. (d)

Sol.

53. In the reaction p + n p + K⁺ + X mediated by strong interaction, the baryon number B, strangeness S and the third component of isospin I₃ of the particle X are, respectively

(a) –1, –1 and –1

(b) +1, –1 and –1

(c)

(d) –1, –1 and 0

Ans. (b)

Sol. p + n p + K⁺ + X

54. In an elastic scattering at an energy E, the phase shifts satisfy δ₀ ≈ 30°, δ₁ ≈ 10° while the other phase shifts are zero. The polar angle at which the differential cross section peaks is closest to

(a) 20°

(b) 10°

(c) 0°

(d) 30°

Ans. (c)

Sol. In the partial wave expansion, the differential scattering cross section is given by

where is the scattering angle. Taking Cross section fro l = 0 and l = 1, we have,

Since the differential cross section peaks is do not,

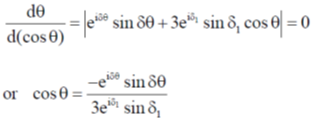
Simplifying above expression

Thus, the closest angle would be 30°.

55. The unnormalized wave function of a particle in one dimension in an infinite square well with walls at x = 0 and x = a, is = x(a – x). If is expanded as a linear combination of the energy eigenfunctions, dx is proportional to the infinite series

You may use dt = –a cos a + sin a and dt = –2 – (a² – 2) cos a + 2a sin a

(a)

(b)

(c)

(d)

Ans. (a)

Sol. We have

The normalization constant is determined at follows.

Thus, the normalised wave function is given by

Multiply the above equation by and integral to determine coefficient C_n,

Let change of variable y =

Employing integral

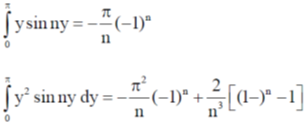
We get

Probability P_n is given by

One can see that P_n is proportional to n^–6, this is assessable in option (1). Hence the correct series would by