1. Let x be a non-empty set and P(x) be the set of all subsets of x. On P(x), define two operations, * and as follows; for Which of the following is true?

(a)

(b)

(c)

(d)

Ans. (c)

Sol. For consider the operation for this

(i) Binary operation:

(ii) Associativity:

(iii) Identity:

= A

So, s.t. = A.

(iv) Inverse:

So, P(x) is not a group under (*).

Option (c) is correct.

2. Let and for any prime p, let

Which of the following are true?

(a)

(b)

(c)

(d)

Ans. (a), (c)

Sol.

3. Which of the following are true?

(a) Q has countably many subgroups.

(b) Q has uncountably may subsets.

(c) Every finitely generated subgroups of Q is cyclic.

(d) Q is isomoprhic to Q × Q as groups.

Ans. (b), (c)

Sol. (i) Q has uncountably many subgroups.

Let P = {p_i|p_i is is a prime numbers, i = 1, 2, ...} and S = set of all non-empty subsets of P.

We can easily see that S is uncountable.

If bd > 1 and p is prime divisor of bd

(iii) Let G be a finitely generated subgroup of (Q, +) and let g₁, g₂, ..., g_k be non-zero generators of G.

Every finitely generated subgroup of (Q, +) is cyclic.

Option (3) is true.

(iv) Let Q Q × Q

As Q is cyclic group all its subgroup are cyclic.

Now, consider then H is not cyclic.

Option (4) is false.

4. Let R, S be CRU, be a surjective ring homomorphism, Q < S be a non-zero prime ideal. Which of the following are true?

(a) f^–1(Q) is a non-zero prime ideal in R.

(b) f^–1(Q) is a maximal ideal in R if R is a PID.

(c) f^–1(Q) is a maximal ideal in R if R is a finite CRU.

(d) f^–1(Q) is a maximal ideal in R if

Ans. (a), (b), (c), (d)

Sol. Recall:

(1) If R₁ and R₂ are two CRU's and is a ring homomorphism then if I is prime ideal in

(2) If R is finite CRU then every ideal of R is maximal.

(3) Let R be CRU s.t. then every prime ideal is maximal.

(4) In a PID, every non-trivial prime ideal is a maximal ideal.

From all above results, we can see

Option (a), (b), (c) & (d) are true.

5. Which of the following statements is true?

(a)

(b)

(c)

(d)

Ans.

Sol. For this type of problems, just try to discard given options by taking suitable counter examples.

For option (1), let n = 16 then (n – 1)! + 3 = 15! + 3 = even + odd = odd

For option (2). Take n = 17 then

For option (4), take n = 16 then n² = 16² & n! + 1 = 16! + 1.

Here 16² is even while 16! + 1 is odd integer.

For option (3), true [For understand, consider any even].

Note: Proof for this option is two long, so just try to understand with example.

But p₂ is also a prime, so not divisible by any of integer except 1.

These of one prime factor is 2, then n has at most two distinct prime factor else one.

Thus, option (3) true.

For option (4). Recall if m & n one co-prime then

Here, if n, k are co-prime Result obviously true.

Other case: Assume that gcd(n, k) 1

In that case, write in prime factorization form after that above case will be applicable.

Note: op(3) & op(4) is direct result in number theory.

To remember result results, just practice them in advance, it will save your time in exam.

6. Let A be a 2 × 2 real matrix with det A = 1 and trace A = 3. What is value of trace A²?

(a) 2

(b) 10

(c) 9

(d) 7

Ans. (d)

Sol. Method-I:

Method:

Then Eigenvalues of A² are

7. Let A and B be 2 × 2 matrices. Then which of the following is true?

(a) det(A + B) + det(A – B) = det(A) + det(B)

(b) det(A + B) + det(A – B) = 2 det(A) – 2 det(B)

(c) det(A + B) + det(A – B) = 2 det(A) + 2 det(B)

(d) det(A + B) – det(A – B) = 2 det(A) – 2 det(B)

Ans. (c)

Sol. Method-I:

Method:

So, option (3) is true.

8. Which of the following real quadratic forms on R² is positive definite?

(a) Q(x, y) = xy

(b) Q(x, y) = x² – xy + y²

(c) Q(x, y) = x² + 2xy + y²

(d) Q(x, y) = x² + xy

Ans. (b)

Sol. Recall:

So, option (a), (c) and (d) are false and option (2) is true.

Method-II:

(1) Matrix representation for Q(x, y) = xy is

So, its all eigenvalue cannot be positive.

Option (1) is false.

All eigen values of A are positive.

Quadratic form is positive definite.

One eigenvalue of A is zero and other is 2.

One eigenvalue are not positive.

Q(x, y) is not positive definite.

Option (3) is false.

All eigenvalues cannot be positive.

Q(x, y) is not positive definite.

Option (4) is false.

9. Let A be an n × n matrix such that the set of all its non-zero eigenvalues has exactly r elements. Which of the following statements is true?

(a)

(b)

(c)

(d) A² has r distinct non-zero eigenvalues

Ans. (c)

Sol. Method-I:

In question, A has r eigenvalues (non-zero).

But A² has eigenvalues –1, –1 which are not distinct.

Option (4) is false.

Method-II:

Then Jordan canonical form of A is

10. If A = then A²⁰ equals

(a)

(b)

(c)

(d)

Ans. (b)

Sol. Method-I:

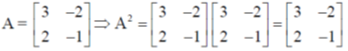
Continuing like this, we observe that

1^st column's entry sign is +ve

and 2^nd column's entry sign is –ve.

So, option (2) true.

Attestation:

In this type of question, try to find a pattern. Don't do so much calculation.

In above question's all options, entries of matrices are same but entries signs are different.

Method-II

Here, each row-sum is = 1 and Trace of A = 2.

nother eigen values = 2 – 1 = 1.

  1, 1 are eigenvalues of A.

Then eigenvalues of A²⁰ = 1, 1 det(A²⁰) = 1.1 = 1.

Now,

Also in option (4), det(A²⁰) = –2.40² + 1.

Option (3), (4) is false.

Recall: If sum of each row of A is C then sum of each row in Aⁿ is Cⁿ.

Sum of each row in A = 1.

Sum of each row in A²⁰ = 1²⁰ = 1.

So, option (1) is discarded. Also from here, option (3), (4) discarded here.

Option (2) is true.

11.

(a) a > 0, b > 0

(b) ab > 0

(c) a = 0, b = 0

(d) for no value of a, b

Ans. (d)

Sol. Method-I:

P(x, y) is bilinear transform the matrix representation of p(x, y) is A = .

If P(x, y) is defining an inner product if A is positive definite i.e. all eigenvalues of A are positive.

Option (4) is true.

Method-II:

Here, a > 0, b > 0. So option (1) discarded.

a, b > 0, so option (2) discarded.

And If we take a = 0 then

p(x, y) = b²x₂²

then p((1, 0)), (1, 0) = 0

So, p(x, y) not forms inner product space.

Similarly, for b = 0, p(x, y) not forms inner product space.

Option (3) false.

Option (4) true.

12. Let Q(x, y, z) be a real quadratic form. Which of the following statements are true?

(a) Q(x₁ + x₂, y, z) = Q(x₁, y, z) + Q(x₂, y, z) x₁, x₂, y, z.

(b) Q(x₁ + x₂, y₁ + y₂, 0) + Q(x₁ – x₂, y₁ – y₂, 0) = 2Q(x₁, y₁, 0) + 2Q(x₂, y₂, 0), x₁, x₂, y₁, y₂.

(c) Q(x₁ + x₂, y₁ + y₂, z₁ + z₂) = Q(x₁, y₁, z₁) + Q(x₂, y₂, z₂) for at least one choice of x₁, x₂, y₁, y₂, z₁, z₂.

(d) 12Q(x₁ + x₂, y₁, y₂, 0) + 2Q(x₁ – x₂, y₁ – y₂, 0) = Q(x₁, y₁, 0) + Q(x₂, y₂, 0), x₁, x₂, y₁, y₂.

Ans. (b), (c)

Sol. (1) Let Q(x, y, z) = x² then it is a real quadratic form.

But Q(x₁, y, z) + Q(x₂, y, z) = x₁² + x₂² (x₁ + x₂)² = Q(x₁ + x₂, y, z)

Option (a) false.

(3) if x₁ = x₂ = y₁ = y₂ = z₁ = z₂ = 0 then Q(0, 0, 0) = Q(0, 0, 0) + Q(0, 0, 0) = 0

(4) Let Q(x, y, z) = x² then Q(x₁ + x₂, y₁ + y₂, 0) = (x₁ + x₂)²

So, 2Q(x₁ + x₂, y₁ + y₂, 0) + 2Q(x₁ – x₂, y₁ – y₂, 0) = 2(x₁ + x₂)² + 2(x₁ – x₂)²

and Q(x₁, y₁, 0) + Q(x₂, y₂, 0) = x₁² + y₂²

2Q(x₁ + x₂, y₁ + y₂, 0) + 2Q(x₁ – x₂, y₁ – y₂, 0) Q(x₁, y₁, 0) + Q(x₂, y₂, 0)

Option (4) false.

(2) Q(x₁ + x₂, y₁ + y₂, 0) = a(x₁ + x₂)² + b(y₁ + y₂)² + c(x₁ + x₂) (y₁ + y₂)

and Q(x₁ – x₂, y₁ – y₂, 0) = a(x₁ – x₂)² + b(y₁ – y₂)² + c(x₁ – x₂) (y₁ – y₂)

then Q(x₁ + x₂, y₁ + y₂, 0) + Q(x₁ – x₂, y₁ – y₂, 0)

= ax₁² + ax₂² + 2ax₁x₂ + by₁² + by₂² + 2by₁y₂ + cx₁y₁ + cx₁y₂ + cx₂y₁ + cy₂x₂

+ ax₁² + ax₂² – 2ax₁x₂ + by₁² + by₂² – 2by₁y₂ + cy₁x₁– cx₁y₂ – cx₂y₁ + cy₂x₂

= 2(ax₁² + by₁²) + (cy₁ x₁) + 2(ax₂² + by₂² + cy₂x₂)

= 2Q(x₁, y₁, 0) + 2Q(x₂, y₂, 0), x₁, x₂, y₁, y₂.

Option (2) true.

13. Let P be a square matrix such that p² = p? Which of the following statements are true?

(a) Trace of p is an irrational number.

(b) Trace of p = rank of p.

(c) Trace of p is an integer.

(d) Trace of p is an imaginary complex number.

Ans. (b), (c)

Sol. Method-I:

We have p² = p then annihilating polynomial for p = x² – x and minimal polynomial = m_A(x)/x² – x then the m_A(x) = x or x – 1, x(x – 1) then possible eigenvalues of p are 0 or 1.

So, option (a) and (d) are false.

Now, in minimal polynomial each factor is linear.

P is diagonalizable matrix then diagonal matrix similar to p is .

(According to possibilities of m_A(x) then in each case.

Trace of p = rank of p and also tr(p) is an integer.

Option (b), (c) are true.

Method-II: p² = p.

P is an idempotent matrix and eigenvalues of an idempotent matrix 0 or 1.

Also, idempotent matrix is diagonalizable.

Possible diagonal matrix similar to p

Tr(p) = rank p in each case.

Also, tr(p) = 0 or 1 or 2.

Option (b), (c) true and option (a) and (d) false.

14. Let n be a positive integer and F be a non-empty proper subset of {1, 2, ..., n}.

(a)

(b)

(c)

(d)

Ans. (a), (b)

Sol.

So, option (a), (b) true and option (c), (d) is false.

15. Let A be an n × n matrix such that the first 3 rows of A are linearly independent and the first 5 columns of A are linearly independent. Which of the following statements are true?

(a) A has at least 5 linearly independent rows

(b)

(c)

(d)

Ans. (a), (c)

Sol.

Option (a) true.

a 5 × 5 sub matrix of A such that It's 5 columns and rows are linearly independent i.e. it is invertible.

16. Let be a non-zero vector. Define a linear transformation where x·y denotes the standard inner product in R³. Which of the following statements are true?

(a) The eigenvalues of T are +1, –1.

(b) The determinant of T is –1.

(c) The trace of T is +1.

(d) T is distance P reserving.

Ans. All

Sol.

Then for v = (1, 0, 0).

Option (a), (b) and (c) are true.

17. A quadratic form Q(x, y, z) over R represents 0 non trivially if there exists (a, b, c) /{0, 0, 0} such that Q(a, b, c) = 0. Which of the following quadratic forms Q(x, y, z) over R represents 0 non-trivially?

(a) Q(x, y, z) = xy + z²

(b) Q(x, y, z) = x² + 3y² – 2z²

(c) Q(x, y, z) = x² – xy + y² + z²

(d) Q(x, y, z) = x² + xy + z²

Ans. (a), (b), (d)

Sol. (1) Q(1, –1, 1) = –1 + 1 = 0

Option (a) is true.

Option (b) is true.

(4) Q(1, –2, 1) = 1 – 2 + 1 = 0

Option (c) true.

Q(x, y, z) = 0

Q(x, y, z) = x² – xy + y² + z² = does not represent 0 non-trivially.

Option (3) false.

18. Let A and B be n × n real matrices and let C = . Which of the following statements are true?

(a)

(b)

(c)

(d) All eigenvalues of C are real.

Ans. (a), (b)

Sol.

(3) Let A = [1], B = [0]

  then C =

Here eigen value of B is '0' but '0' is not eigen value of C.

Option (c) fasle.

(4) Let A = , B = [0]_{2 × 2}

  then C = then Ch_A(x) = (x² + 1) (x² + 1) = Ch_A(x) Ch_A(x)

Eigenvalues of C are ±i, ±i which are not real.

Option (d) false.

19. Let A be an n × n real matrix. Let b be an n × 1 vector. Suppose Ax = b has no solution. Which of the following statements are true?

(a) There exists an n × 1 vector C such that Ax = c has a unique solution.

(b) There exist infinitely many vectors C such that Ax = C has no solution.

(c) If y is the first column of A then Ax = y has a unique solution.

(d) det A = 0.

Ans. (b), (d)

Sol. Recall:

Option (d) is true.

(2)  If we take, c = kb, for infinitely many values of k, then Ax = kb has no solution.

(3)  If y is the first column of A then rank(A) will not be affected.

And if Ax = b has no solution then Ax = y has no solution.

Option (c) false.

20. Which of the following statements is true?

(a) There are at most countably many continuous maps from R² to R.

(b) There are at most finitely many its surjective maps from R² to R.

(c) There are infinitely many its injective maps from R² to R.

(d) There are no its bijective maps from R² to R.

Ans.

Sol.

So, we cannot establish 1-to-1 correspondence between then so (there not exist) any bijective maps from R to R².

Option (d) is true.

Other approach

So, option (a) is false.

Option (b) is false.

Trick: now analysis the options.

Since option (b) < option (a) and option (c) < option (a) and if option (b) or option (c) become true then option (1) will be also true which is not possible because this question is from part-B.

Also, we already shown that option (1) is false.

Option (d) only left so true.

21. Given (a_n)_{n > 1} a sequence of real number solution.

Which of the following statement is true?

(a)

(b) There is a subsequence

(c) There is a number b s.t.

(d) There is a number b and a subsequence

Ans. (d)

Sol. Tips: Try to discard options by taking suitable choice for

Option (1): Let

Option (3) and option (4): (NB may be you have to try with more than one sequence =

But here fixed b s.t. above series become cgt. You may take b = 1/2 or –1/2 but not both otherwise uniqueness will be lost.

22. The series converges

(a) only for x = 0

(b)

(c) uniformly only for

(d)

Ans. (d)

Sol. Here given

Note: In CSIR-NET many times question has been asked based on M_n-test/uniformly convergences.

Result:

Wariness M-test: A series of fⁿ will converges uniformly (absolutely) on [a, b] if it's a convergent series of '+ve' no s.t. |f_n(x)|

23. Which of the following statement is not true?

(a)

(b)

(c)

(d)

Ans. (c)

Sol. Tips: Don't proceed with theoretical approach. Try to choose a suitable example and discard options.

Consider f(x) = 1. This fⁿ satisfies the question i.e. bounded fⁿ and from

Option (3) is not true and option (4) is true.

Thus, correct answer is option (c).

24. Given f, g are continuous on [0, 1] s.t. f(0) = f(1) = 0, g(0) = g(1) = 1 and f(1/2) > g(1/2). Which of the following statements is true?

(a)

(b)

(c)

(d)

Ans. (c)

Sol. Think geometrically (Try to draw given condition).

Given f(0) = f(1) = 0, g(0) = g(1) = 1

f(1/2) > g(1/2)

from geometrically it is clear that there is at least two points where f & g intersects. Option (3).

Note: You may also draw like here, I want to just say that any how for will draw, you find that they intersects at finite no. of point and in fact at even no. of points.

Thus, option (3) true.

25.

Which of the following statements is true?

(a)

(b)

(c)

(d)

Ans. (c)

Sol.

Now, try to discard options by taking suitable example.

Let E_n = {{0}, {1}, {0}, {1}, …}

For option (2, 3, 4)

Recall: Differential of limit of a sequence.

So, from above remark/note.

Option (2) false and option (3) true and option (4) false.

26.

(a)

(b)

(c)

(d)

Ans. (b), (c)

Sol. This type of question has been many times asked in CSIR-NET GATE & SET, and also it is easy & scoring question.

(uncountable) & (countable)

Thus, option (2) and option (3) true.

27. Which of the following statements are true? The series _________.

(a)

(b)

(c)

(d)

Ans. (a), (d)

Sol.

How Recall Leibnitz's Test for alternating series here

opt(2). By Leibnitz test it will be convergent

But it is not absolutely convergent as divergent by p-test (for p = 1)

So, opt(2) false.

Note: If any divergent, series appears in summation then that summation becomes divergent.

Thus, (*) is divergent opt(3) false.

Convergent by Leibnitz test convergent by p-tese.

Option (4) is true.

Option (1) and option (4) are true.

28. Let f(x) = e^–x and g(x) = e^–x2. Which of the following statements are true?

(a)

(b)

(c)

(d)

Ans. (b), (c), (d)

Sol.

Since e^–x is mirror image of e^x, so both have same behavior.

29. Consider two series A(x) =

Which of the following statements are true?

(a) Both A(x) & B(x) converge point wise.

(b) Both A(x) & B(x) converge uniformly.

(c) A(x) converge uniformly but B(x) does not.

(d) B(x) converge uniformly but A(x) does not.

Ans. (a), (d)

Sol. Since at x = 0 & 1 A(x) = 0

Next on (0, 1) is convergent on (0, 1)

So, by comparison, is convergent on (0, 1) thus A(x) is point wise convergent on [0, 1]

For uniformly,

As we know that uniformly.

Convergent fⁿ converge to convergent fⁿ

A(x) doesn't converge uniformly.

Now for B(x): (Work similar to A(x)) thus at x = 0 and 1, B(x) = 0 and for

For uniformly [Recall: Dirchlet test]

Dirchled's Test let

Now, tank a_n = (–1)ⁿ and b_n = xⁿ(1 – x).

Here xⁿ(1 – x) is point-wise convergent.

Now, we have to check for uniformly.

Now put x = , then

Thus, here B(x) is pointwise as well as uniformly.

Hence, option (1, 4) correct.

30. Let be defined by f(x, y) = .

Define g(x, y) = .

Which of the following statements are true?

(a)

(b)

(c) g is not a well-defined fⁿ.

(d)

Ans. (a), (d)

Sol. f(x, y) = at origin, f is not cts.

We have to analysis g = .

Recall: Waitress M-test

Now, we have to check boundedness.

(Hint: For checking boundedness you many use polar form).

Thus, k = 1 hence M_n = 1/2ⁿ which GP (Geometric Progression)

and g(x, y) is also cts. There where f(x, y) is cts and a/c statement f is cts. Everywhere except origin.

If all these f will be cts. then by waitress M test, it's uniform limit will be cts.

Case-I: Assume that then c – i ± 0, i = 1, 2, 3, ... hence f(c – 1, y – 1), f(c – 2, y – 2), ... will be convergent and uniformly limit of cts. fⁿ is cts.

Since all f on RHS one cts so their uniform limit will be also cts.

So, from both case, option (1) correct.

31. Suppose that {f_n} is a sequence of real-valued fⁿ on R. Suppose it converges to a continuous fⁿf uniformly on each closed and b.dd subset of R. Which of the following statements are true?

(a) The sequence {f_n} converges to f uniformly on R.

(b) The sequence {f_n} converges to f point wise on R.

(c) For all sufficiently large n, the function f_n is bounded.

(d) For all sufficiently large n the fⁿ f_n is cts.

Ans. (b)

Sol.

Try to discard options by taking suitable choice let f_n(x) = converges on R but not uniformly.

Not uniformly because this example satisfy the condition f question i.e. over a b.dd set x is b.dd by k then sup uniformly on any compact set.

Thus, option (1) is incorrect.

For opt (2) (We have to assume that is convergent at every point or not)

Now choose any arbitrary point on R, say x₀ then it will lie (definitely) in some close + b.dd set & a/c to question its cgs to in closed + b.dd set. they whatever you choose arb. point that will lie in a closed + b.dd set hence convergent.

Hence cgs. to f point wise on R.

opt(2) correct.

Opt(3) Consider example taken in op (1).

Option (4) consider the example

(Here f₁, f₂, f₃, ... all are discontinuous function)

Thus this question satisfies all the condition of question.

But this f_n(x) is not continuous.

32.

Which of the following statements are true?

(a) I_p is convergent for p = –1/2

(b) I_p is divergent for p –3/2.

(c) I_p is convergent for p = 4/3

(d) I_p is divergent for p = –4/3.

Ans. All

Sol. Recall: Improper integrals & their convergence nature.

(2) (Comparison test). If f & g are cts non-negative function on [a, b] s.t. then

i.e. both cgs or dgs simultaneously.

Now solving options one-by-one

So, by comparison test is also convergent option (1) is true.

Tips: Don't proceed like option (1) because is not cgf so you can't decide.

So both will converges/diverge simultaneously.

33. Define f(x, y) = .

Which of the following statements are true?

(a) f is continuous at (0, 0).

(b) f is bounded in nb.d of (0, 0).

(c) f is not bounded in any nb.d of (0, 0).

(d) f has all directional derivatives at (0, 0).

Ans. (b)

Sol. We have given f(x, y) for continuity just took on limit along different path, i.e. path dependent or not.

Take y = mx then

It depends on m (i.e. path dependent)

So, f is not continuous at (0, 0) option (a).

For option (4),

Recall: Directional derivative of 2-tuble directional derivative of f at (a, b) in direction of u = (u, u) is given by

Now, apply on above problem

Thus, directional derivative doesn't exists at (0, 0).

Option (4) is false.

Next option (2) and (3) are related.

As from option (1) we observed that limit at (0, 0) is path dependent. It gives some values so obviously it is bounded.

Option (2) is true and option (3) is false.

How (Check using iterated limit)

Here limit are not equal but bounded.

Other method (by using polar form)

34. Define f(x, y) = .

Which of the following statements are true?

(a) f is discontinuous at (0, 0).

(b) f is continuous at (0, 0).

(c) all directional derivative of at (0, 0) exist.

(d) f is not differentiable at (0, 0).

Ans. (b), (c), (d)

Sol. opt(1) & opt(2) are related

For continuity, check it is path dependent or not put y = mx then as thus

therefore, clearly f is continuous at origin.

(Note: for continuity you may use method)

But it is time taking

op(1) false, op(2), correct.

For op(3) (Recall: Directional derivative)

D.D of f at (a, b) in directional of u = (u₁, u₂) is

thus, it is clearly existing for every (u₁, u₂)

Option (3) is true.

For option (4):

(Recall, sufficient condition of differentiability) & fⁿ f(x, y) is said to be differential at (a, b)

thus,

35.

p(x, y) = .

Which of the following statements are true?

(a) p(x, y) = 0 iff x = y = 0

(b)

(c)

(d)

Ans. (a), (b), (c)

Sol.

Let's understand with numerical example

let x₁ = 3, x₂ = –3, y₁ = 4, y₂ = 5 then

p(3 – 3, 4 + 5) = p(0, 9) = |9| = 9

while p(x₁, y₁) + p(x₂, y₂) = p(3, 4) + p(–3, 5) = |3| + |–3| = 6

36.

Which of the following are true?

(a) f has finitely many zeros.

(b) f has a sequence of zeros that converges to a removable singularity of b.

(c) f has a sequence of zeros that converges to a pole of f.

(d) f has a sequence of zeros that converges to an essential singularity of f.

Ans. (d)

Sol.

Also, limit point of zeros of function f(z) is an isolated essential singularity.

opt(4) true opt(2), (3) false.

37. Let be the positively oriented circle in the complex plane given by The line integral equals

(a)

(b)

(c)

(d)

Ans. (a)

Sol. Here g(z) = then zeros of z² – 1 are 1 + –1.

38. Let be the positively oriented circle in the complex plane given by Then equals

(a) 3

(b) 1/3

(c) 2

(d) 1/2

Ans. (b)

Sol. Recall: Cauchy Integral Formula:

Let f be analytic on D,

where is winding no. of around a and is a positively oriented circle.

Here g(z) =

then

Roots of (z – 1)(z² + z + 1) are

Option (2) is true.

39. Let p be a positive integer. Consider the closed curve r(t) = e^it, Let f be a function holomorphic in {z : |z| < R} where R > 1. If f has a zero only at z₀, 0 < |z₀| < R and it is of multiplicity q then equals

(a)

(b)

(c)

(d)

Ans. (a)

Sol. Recall: Modified Argument Principal

Let f be a holomorphic function with no zeros on the boundary of some simply connected region D and N + P denotes the number of zeros and poles of f inside D respectively, counted with multiplicity.

Then, for an analytic

where, n(D, z) = winding number of D around z,

and a_i = all zeros of f with multiplicity & b_i = poles of f with orders.

Here, we have given, f has zero only at z₀, 0 < |z₀| < R.

Option (1) is true.

40. Let f be a holomorphic function on the open unit disc Suppose that on D and f(0) = i. Which of the following are possible values of

(a) –i

(b) i

(c) 1

(d) –1

Ans. (b)

Sol. Recall: Minimum Modulus Theorem

Let f(z) be a non-zero, non-constant function on a domain D and f(z) is analytic in D.

Then minimum value of |f(z)| occurs on the boundary of D.

Minimum value of f(z) is obtained inside D.

41. Let n be a positive. For a real number R > 1 let

The set contains which of the following sets?

(a)

(b)

(c)

(d)

Ans. (c)

Sol.

Option (3) is true.

42. Let be the open unit disc and let be a holomorphic function. Suppose that f(0) = 0 and Which of the following are possible value of

(a)

(b)

(c)

(d)

Ans. (a), (b)

Sol. Recall: Schwarz's Lemma (Extension)

In question, given that is holomorphic function and and let f(z) has zero of order at least

By extension of Schwarz's Lemma, for n = 2

And for n > 2, we can observe

and all possible values will not be outside of

Option (3), (4) is false.

43. The general solution of the equation is _________.

(a)

(b)

(c)

(d)

Ans. (a)

Sol. Given i.e. xp + yq = 0

on comparing with Pp = Qq = R we have P = x, Q = y and R = 0.

44. The general solution of the surfaces which are perpendicular to the family of surfaces z² = kxy, is _________.

(a)

(b)

(c)

(d)

Ans. (c)

Sol.

Now, we will solve it using Lagrange A.E.

Other possible form of solution are when c₁ and c₂ calculated

So, first try to understand the concept then you will easily take this type of problems (mostly asked).

45. Consider the PDE

Which of the following statements are true?

(a) Equation (i) is parabolic for y > 0 & elliptic for y < 0.

(b) Equation (i) is hyperbolic for y > 0 & elliptic for y < 0.

(c) Equation (ii) is elliptic in I & III quadrant and hyperbolic in II & IV quadrant.

(d) Equation (ii) is hyperbolic in I & III and elliptic in II and IV quadrant.

Ans. (b), (c)

Sol. Here, for (i) A = 1, B = 2, C = 1-sgn(y)

Now check B² – 4AC

Option (1) is incorrect (2) is correct.

For (ii) here A = y, B = 0, C = x

B² – 4AC = 0 – 4yx = –4xy.

Now analyses B² – 4AC in different quadrant.

In quadrant I and III, x and y are of same eigen sign

While in quadrant II and IV x and y are of opposite sign

46. Consider the PDE z = Which of the following statements are true?

(a) The complete integral is z = xa + yb + ab, a, b arbitrary constant.

(b) The complete integral is z = xa + yb + , a, b arbitrary constant.

(c) The particular solution passing through x = 0 and z = y² is

(d) The particular solution passing through x = 0 and z = y² is

Ans. (a), (c)

Sol.

So, it's complete integral is z = ax + by + ab or xa + yb + ab.

Option (1) is correct and 2 is incorrect.

Now for option (3) and option (4).

Given x = 0 and z = y².

Now, we have to find value of t.

So, different (3) w.r.t., we get 2t – b = 0

Now put t = b/2 in equation (3),

Now put value of a in equation (2)

Now, to eliminate b different (4) w.r.t. b and find value in terms of x and y.

Now put this b in equation (4) and simplify

47. The solution of the Fredholm integral equation y(s) = is

(a) y(s) = –(50s + 40s²)

(b) y(s) = (30s + 15s²)

(c) y(s) = (30s + 15s²)

(d) y(s) = (60s + 50s²)

Ans. (c)

Sol.

Now solving equation (4) and (5) to find c₁ and c₂.

Note: Many times question like this has been asked in CSIR-NET and SET Exam.

48. For the Fredholm integral equation (IE)

Which of the following statements are true?

(a) It has a non-trivial solution satisfying

(b) Only the trivial solution satisfies

(c) It has non-trivial solution for all

(d) It has non-trivial solution only if

Ans.

Sol.

For option (1) and 2.

i.e. c = 0 then by (1) y(s) = trivial solution.

49. Let k be a positive integer. Consider the differential equation

Which of the following is true?

(a) It has a unique solution which is continuously differential on

(b) It has at most two solution which are continuously differential on

(c) It has infinitely many solution which are continuously differential on

(d) It has no continuously differential solution on

Ans.

Sol. Recall:

If

then the differential equation has infinite number of independent solution.

Given differential equation has infinite number of solution.

Option (c) is true.

50. Let y₀ > 0, z₀ > 0 and Consider the following two differential equations

We say that the solution to a differential equation exists globally if it exists for all t > 0. Which of the following statements is true?

(a) Both (*) and (**) have global solutions.

(b) None of (*) and (**) have global solutions.

(c) There exists a global solution for (*) and there exists a

(d) There exists a global solution for (**) and there exists a

Ans. (d)

Sol.

Option (4) is true.

51. The following two-point boundary value problem

has a trivial solution y = 0. It also has a non-trivial solution for

(a)

(b)

(c)

(d)

Ans. (b), (c)

Sol.

so y = 0 is trivial solution.

52. Consider the solutions y₁ = to the homogeneous linear system of differential equation

Which of the following statements are true?

(a) y₁ and y₂ form a basis for the set of all solutions to (*).

(b) y₁ and y₂ are L.I. but do not form a basis for the set of all solutions to (*).

(c) There exists another solution y₃ such that {y₁, y₂, y₃} form a basis for the set of all solutions to (*).

(d) y₁ and y₂ are linearly dependent.

Ans. (b), (c)

Sol. Recall: then solution of this is given by where are eigenvalues of A_{3 × 3} and v₁, v₂ and v₃ are corresponding eigenvectors respectively.

Here in y₁ and y₂, e^–3t and e^–5t factor is coming.

Claim: –3 + –5 are eigenvalues of A_{3 × 3}.

So, v₃ = (1, 0, 1)^T then y₃ = then {y₁, y₂, y₃} forms a basis for the set of solution (*).

Option (3) is true option (1) is false.

53. Let A be an n × n matrix with distinct eigenvalues with corresponding linearly independent eigenvectors {v₁, ..., v_n}. Then, the non-homogeneous differential equation =

(a)

(b)

(c)

(d)

Ans. (a), (c)

Sol.

54. The extremal of the functional J(y) = is

(a)

(b)

(c)

(d)

Ans. (d)

Sol.

Recall: Euler's equation

Now, integrate both side (two times)

Now, apply B.C₀ —

55. Consider the functional J(y) = with B.C

(a)

(b)

(c)

(d)

Ans. (b), (c)

Sol.

56. The extremal of the functional J(y) = is of the form

(a)

(b)

(c)

(d)

Ans. (b)

Sol. Here

So by Euler's equation

Here B.C. is not given.

So, use transverse city constant

57. For Consider the iteration defined by

The above iteration has two distinct fixed points.

Which of the following statements are true?

(a) The iteration (*) is equivalent to the recurrence relation x_{k + 1} – r₁ = 1/2(r_k + r₁) (r_k – r₁),k = 0, 1, 2, ....

(b) The iteration (*) is equivalent to the recurrence relation x_{k + 1} – r₁ = 1/2(x_k + r₂) (x_k – r₁), k = 0, 1, 2, ....

(c)

(d)

Ans. (a), (c), (d)

Sol.

Now, checking options one by one

So, option (1) is true.

(Hint: Now think values of r₁ & r₂ s.t 0 < r₁ < 1 < r₂) and above 1 not < 1

Whose two distinct roots are r₁ & r₂ s.t. 0 < r₁ < ₁ < r₂

So, (l – r₁) (l – r₂) = 0

58. The maximum and minimum values of 5x + 7y, when |x| + |y| < 1 are ______.

(a) 5 and –5

(b) 5 and –7

(c) 7 and –5

(d) 7 and –7

Ans. (d)

Sol. Here corner's points are (1, 0) (0, 1), (–1, 0) & (0, –1)

Let z = 5x + 7y

59. Suppose that |3x| + |2y| < 1. Then the max. value of 9x + 4y is _______

(a) 1

(b) 2

(c) 3

(d) 4

Ans. (c)

Sol. Here extreme points are (1/3, 0), (–1/3, 0), 0, 1/2), (0, –1/2)

Let z = 9x + 4y, then

60. Consider a markov chain with transition probability matrix

Let Then which of the following statements are correct?

(a)

(b)

(c)

(d)

Ans. (a)

Sol. Let state space = {1, 2, 3, 4, 5}

Now draw the state transition diagram.

Hence given chain is a periodic opt(3). Incorrect.

Recall: Irreducible markov chain

If all states of a markov chain communicate with each other then that markov chain is irreducible.

Come to the question: Here all states not communicate with each other (e.g. no communication b/w {1, 3, 5} to {2, 4} hence reducible

pt(4) incorrect.

Result: A finite reducible markov chain admits infinite stationary distribution.

But a/c to op(2). if is any distribution then if means. it have unique st. distribution.

Which is contradiction. opt(2). Incorrect.

Thus only opt(1). left opt(1). correct.

How opt(1). true.

Recalls: If is a stationary distibution then

61. Consider a Markov Chain with a countable state space s. Identify the correct statements.

(a) If the markov chain is a periodic & irreducible the a stationary distribution.

(b) If the markov chain is a periodic & irreducible then there is at most one stationary distribution

(c) If S is finite then a stationary distribution.

(d) If S is finite then there is exactly one stationary distribution.

Ans. (b), (c)

Sol. Let S be a countable state space: