PYQ DEC 2018 - VedPrep

CSIR NET MATHEMATICS (DEC - 2018)
Previous Year Question Paper with Solution.

(i) f(0) = 0

(ii) f(r) =

Then the map f is

(a) one-to-one and onto

(b) not one-to-one, but onto

(d) neither one-to-one nor onto

Ans. (d)

Sol.

So, f is not onto.

Hence, f is neither one-one nor onto.

Option (d) is correct.

2. Let x be a real number such that |x| < 1. Which of the following is false?

(a)

(b)

(c)

(d)

Ans. (c)

Sol. Let x be a real number such that |x| < 1.

as difference of rationals is again rational and 1/rational is again rational.

3. Suppose the (x_n) is a sequence of real numbers satisfying the following. For every ε > 0, there exists n₀ such that The sequence {x_n} is

(a) bounded but not necessarily Cauchy

(b) Cauchy but not necessarily bounded

(d) not necessarily bounded

Ans. (d)

Sol.

Then

(a) L = 0 if c > 3

(b) L = 1 if c = 3

(d)

Ans. (b)

Sol.

Option (b) is correct.

5. Consider the function tan x on the set

We say that it has a fixed point in S if such that tan x = x. Then

(a) there is a unique fixed point.

(b) there is no fixed point.

(d) there are more than one but finitely many fixed points.

Ans. (c)

Sol. Consider the function "tan x" on the set

as we draw y = tan x and y = x then all intersection points will be fixed points.

In the set S there are infinitely many fixed points.

Option (c) is correct.

6. Define f(x) = for x > 0. Then f is uniformly continuous

(a)

(b)

(d) only on intervals of the form [a, b] for

Ans. (b)

Sol.

if we select r > 0 fixed number then

7. Consider the subspaces W₁ and W₂ and R³ given by

(a) W = span {(0, 1, –1), (0, 1, 1)}

(b) W = span {(1, 0, –1), (0, 1, –1)}

(d) W = span {(1, 0, –1), (1, 0, 1)}

Ans. (a)

Sol.

Hence, option (a) is correct.

If T[C] represents the matrix of T with respect to the basis C then which among the following is true?

(a)

(b)

(c)

(d)

Ans. (c)

Sol.

Option (b) and (d) are incorrect.

Option (c) is correct.

Then which among the following is true?

(a) dim(W₁) = 1

(b) dim(W₂) = 2

(c)

(d) dim(W₁ + W₂) = 3

Ans. (c)

Sol.

will contain common point and one free variable is common in both W₁ and W i.e., W.

Option (c) is correct.

10. Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denote the inverse of A + iI_n. Then all eigen values of (A – iI_n)B are

(a) purely imaginary

(b) of modulus one

(d) of modulus less than one

Ans. (b)

Sol. Given A is n × n complex & self adjoint matrix.

i.e., 1 + is of modulus one.

Hence, option (b) is correct.

11. Let (u₁, u₂, ...., u_n) be an orthonormal basis of Cⁿ as column vectors. Let M = (u₁, ..., u_k), N = (u_{k + 1}, ..., u_n) and P be the diagonal k × k matrix with diagonal entries Then which of the following is true?

(a)

(b)

(d) Rank (MM* + NN*) < n

Ans. (b)

Sol.

Option (c) is wrong.

12.

Which of the following is true?

(a) B is a linear transformation

(b) B is a positive definite bilinear form

(d) B is neither linear nor bilinear

Ans. (b)

Sol.

13. Let R denote the radius of convergence of the power series . Then

(a) R > 0 and the series is convergent on [–R, R].

(b) R > 0 and the series converges at x = –R.

(d) R = 0

Ans. (c)

Sol. Given series

Option (c) is correct.

14.

Then

(a) Then interior of image (f) is empty.

(b) Image (f) intersects very line passing through the origin.

(d) Image (f) contains all its Image (f)

Ans. (b)

Sol.

15. Consider the polynomials p(z), q(z) in the complex variable z and let

(a)

(b)

(d)

Ans. (c)

Sol.

16. Let be the positively oriented of radius 3 centered at the origin. The value of for which is

(a)

(b)

(c)

(d)

Ans. (a)

Sol.

17. The number of group homomorphisms from the alternating group A₅ to the symmetric group S₄ is

(a) 1

(b) 12

(d) 6

Ans. (a)

Sol.

18. Let p > 23 be a prime number such that the decimal expansion (base 10) of 1/p is periodic with period p – 1 that is with {for all t and for any m, 1 < m < p – 1, .

Let (Z/pZ)^* denote the multiplicative group of integers modulo p. Then which of the following is correct?

(a)

(b)

(c)

(d)

Ans. (c)

Sol.

19. Given integers a and b, let N_{a, b} denote the number of positive inters k < 100 such that k = a (mod 9) and k = b (mod 11). Then which of the following statements is correct?

(a) N_{a, b} = 1 for all integers a and b.

(b) There exist integers a and b satisfying N_{a, b} > 1.

(d) There exist integers a and b satisfying N_{a, b} = 0 and there exist integers c and d satisfying N_{c, d} > 1.

Ans. (a)

Sol.

20. Let X be a topological space and U be a proper dense open subset of X. Pick the correct statement from the following:

(a) If X is connected then U is connected.

(b) If X is compact then U is compact.

(d) If X is compact then X\U is compact.

Ans. (d)

Sol.

21. If y₁(x) and y₂(x) are two solutions of the differential equation ,

Then the Wronskian of y₁(x) and y₂(x) at x = is

(a)

(b) 6

(d)

Ans. (c)

Sol.

22. The critical point (0, 0) for the system

(a) stable spiral point

(b) unstable spiral point

(d) stable node

Ans. (c)

Sol.

23. Let u(x, t) be a function that satisfies the PDE u_xx – u_tt = e^x + 6t, t > 0 and the initial conditions u(x, 0) = sin(x), u_t(x, 0) = 0 for very .

Here subscripts denote partial derivatives corresponding to the variables indicated.

Then the value of is

(a)

(b)

(c)

(d)

Ans. (c)

Sol.

24. Let u(x, t) satisfy the IVP

Then the value of equals

(a) e

(b) p

(d) 1

Ans. (c)

Sol.

25. Let f(x) be a polynomial of unknown degree taking the values

All the fourth divided differences are –1/6.

Then the coefficient of x³ is

(a)

(b)

(d) –1

Ans. (a)

Sol.

26. Consider the function defined on y is piecewise C¹ and y(0) = y(2) = 0. Let y_e be a maximizer of the above functional. Then y_e has

(a) a unique corner point

(b) two corner points

(d) no corner points

Ans. (a)

Sol.

27.

(a)

(b)

(c)

(d) 2e⁴

Ans. (b)

Sol.

28. Consider the two dimensional motion of a mass m attached to one end of a spring whose other end is fixed. Let k be the spring constant. The kinetic energy T and the potential energy V of the system are given by

Then which of the following statements is correct?

(a) r is an ignorable coordinate.

(b) q is not an ignorable coordinate

(d) remains constant throughout the motion.

Ans. (c)

Sol.

29. Let (u_n)_{n > 1} be a sequence of real numbers satisfying the following conditions:

Which of the following statements are necessarily true?

(a)

(b)

(c)

(d)

Ans. (c), (d)

Sol.

For example,

30. Let S be an infinite set. Which of the following statements are true?

(a) If there is an injection from S to N then S is countable

(b) If there is a surjection from S to N then S is countable.

(d) If there is a surjection from N to S then S is countable.

Ans. (a), (d)

Sol. Let S be the infinite set.

Therefore, this statement does not imply firmly that S is countable, if may or may not be.

This is also imply, S may be countable or uncountable. So, this is also not a correct option.

31. Let p_n denote the n^th prime number, when we enumerate the prime numbers in the increasing order. For example, p₁ = 2, p₂ = 3, p₃ = 5 and so on.

Then which of the following are correct?

(a)

(b)

(c)

(d)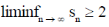

Ans. (a), (b), (c), (d)

Sol.

32. For n > 1, consider the sequence of functions f_n(x) = on the open interval (0, 1). Consider the statements:

(I) The sequence [f_n] converges uniformly on (0, 1).

(II) The sequence [g_n] converges uniformly on (0, 1).

Then,

(a) (I) is true

(b) (I) is false

(d) Both (I) and (II) are true

Ans. (b), (c)

Sol.

superimum of will exist when 2nx + 1 will be minimum and minimum (2nx

i.e., sup M_n will exist when 2n + 1/x will be minimum or 1/x will be minimum on (0, 1) and him

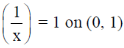
33. Suppose that {f_n} is a sequence of continuous real valued functions on [0, 1] satisfying the following:

Then

(a) {g_n} is Cauchy with respect to the sup norm.

(b) {g_n} is uniformly convergent.

(d)

Ans. (a), (b), (d)

Sol.

34. Given f : a strictly increasing function, we put g(x) = f(x) + f(1/x), Consider a partition P of [1, 2] and let U(P, g) and L(P, g) denote the upper Riemann sum and lower Riemann sum of g. Then

(a) for a suitable f we can have U(P, g) = L(P, g)

(b)

(c)

(d) U(P, g) < L(P, g) for all choices of f

Ans. (a), (b), (c)

Sol.

35. Let f be a real valued continuously differentiable function of (0, 1).

Set is the derivative of f. Let be two consecutive zeros of f. Which of the following statements are necessarily true?

(a) If g(a) > 0, then g crosses the real line from upper half plane to lower half plane at a

(b) If g(a) > 0, then g crosses the real line from lower half plane to upper half plane at a

(c)

(d)

Ans. (b), (d)

Sol.

36. Let A be an invertible real n × n matrix. Define a function by F(x, y) = (Ax, y) where (x, y) denotes the inner product of x and y. Let DF(x, y) denotes the derivative of F at (x, y) which is a linear transformation from Then

(a)

(b)

(c)

(d) If x = 0 or y = 0, then DF(x, y) = 0

Ans. (a), (b), (c)

Sol. Given A is n × n invertible matrix

So, when we will differentiable F(x, y) then to find the derivative w.r.t. to x, we will use first result and for y we will use second result.

37. Let be a function given by f(x, y) = (x³ + 3xy² – 15x – 12y, x + y).

Let : f is locally invertible at (x, y)}. Then

(a)

(b)

(c)

(d)

Ans. (b), (c)

Sol. For locally invertible, we will find point the Jacobian J where J it becomes zero.

That means S will not point (x, y) such that (x – y) = ±1 i.e. two lines y = x ± 1.

Means if (x, y) then we can draw a disc of e-epsilon radius then it will consist infinite point of S.

38. Let X = N, the set of positive integers. Consider the matrices d₁, d₂ on X given by d₁(m, n) = |m – n|, m, n ∊ X

d₂(m, n) = , m, n ∊ X

Let X₁, X₂ denote the metric spaces (X, d₁), (X, d₂) respectively. Then

(a) X₁ is complete

(b) X₂ is complete

(d) X₂ is totally bounded

Ans. (a), (d)

Sol.

39. Let be a linear map that satisfies T² = T – I_n. Then which of the following are true?

(a) T is invertible

(b) T – I_n is not invertible

(d) T³ = –I_n

Ans. (a), (d)

Sol.

40. Let M =

Then which of the following are true?

(a) both systems MX = b₁ and MX = b₂ are inconsistent.

(b) both systems MX = b₁ and MX = b₂ are consistent.

(d) the systems MX = b₁ – b₂ is inconsistent.

Ans. (a), (c)

Sol.

In the question; he is talking about the solution of MX = b₁, MX = b₂ & MX = b₁ – b₂

For consistent system, we have to check the rank of M with rank of

[M : b₁], [M : b₂] & [M : b₁ – b₂]

So, we will try to solve the augmented matrix [M : b₁ b₂ b₁ – b₂]

41. Let M = Given that 1 is an eigenvalue of M then which among the following are correct?

(a) The minimal polynomial of M is (X – 1)(X + 4).

(b) The minimal polynomial of M is (X – 1)²(X + 4).

(d)

Ans. (b), (c)

Sol.

Suppose other two eigenvalues are 1₁ and I₂ then

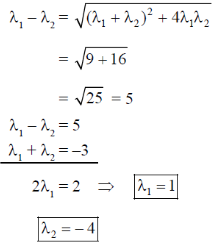
Hence, eigenvalue of M are 1, 1 and –4

In Jordan canonical form, we have only one block of order 2 for eigenvalue 1.

So, in minimal polynomial one factor will be (X – 1)²

Complete minimal polynomial will be

m(X) = (X – 1)²(–X + 4)

Option (A) is false and (B) is true.

and every matrix satisfies its ch. polynomial.

42. Let A be a real matrix with characteristic polynomial (X – 1)³. Pick the correct statements from below:

(a) A is necessarily diagonalizable.

(b) If the minimal polynomial of A is (X – 1)³ then A is diagonalizable.

(d) If A has exactly two Jordan blocks then (A – 1)²is diagonalizable.

Ans. (c), (d)

Sol. Given Ch_A(X) = (X – 1)³

43. Let P₃ be the vector space of polynomials with real coefficients and of degree at most 3. Consider the linear map defined by T(p(x)) = p(x + 1) + p(x – 1)). Which of the following properties does the matrix of T (with respect of the standard basis B = {1, x, x², x³} of P₃} satisfy

(a) det T = 0

(b)

(c)

(d) 2 is an eigenvalue with multiplicity 4

Ans. (d)

Sol.

Form matrix representation, we will find the image of basis elements and try to write them again in their linear combination of basis element of P₃.

So, T(1) = 1 + 1 = 2

= 2.1 + 0.x + 0.x² + 0.x³

T(x) = (x + 1)(x – 1) = 2x

= 0.1 + 2.x + 0.x² + 0.x³

T(x²) = (x + 1)² + (x – 1)²

= x² + 1 + 2x + x² + 1 – 2x

= 2x² + 2

= 2.1 + 0.x + 2x² + 0.x³

T(x³) = (x + 1)³ + (x – 1)³

= x³ + 1 + 3x² + 3x + x³ – 1 – 3x² + 3x

= 2x³ + 6x

= 0.1 + 6.x + 0.x² + 2.x³

44. Let M be an n × n Hermitian matrix of rank k, is an eigenvalue of M with corresponding unit column vector u with then which of the following are true?

(a)

(b)

(c)

(d)

Ans. (a), (d)

Sol.

45. Define a real valued function B on as follows. If v = (x₁, x₂), w = (y₁, y₂) belong to R² define B(u, w) = x₁y₁ – x₁y₂ – x₂y₁ + 4x₂y₂. Let v₀ = (1, 0) and let Then W:

(a) is not a subspace of R².

(b) equals {(0, 0)}.

(d) is the line passing through (0, 0) and (1, 1) .

Ans. (d)

Sol.

46. Consider the Quadratic forms

Q₁(x, y) = xy

Q₂(x, y) = x² + 2xy + y²

Q₃(x, y) = x² + 3xy + 2y²

on R². Choose the correct statements from below:

(a) Q₁ and Q₂ are equivalent

(b) Q₁ and Q₃ are equivalent

(d) all are equivalent

Ans. (b)

Sol. Given Q₁ (x, y) = xy, Q₂ (x, y) = x² + 2xy + y²

Q₃(x, y) = x² + 3xy + 2y²

If we form the matrix for each quadratic form, then it will be

47. Let H denote the upper has plane that is H = {z = x + iy; y > 0}.

For z which of the following are true?

(a)

(b)

(c)

(d)

Ans. (d)

Sol.

48. Let be an analytic function. Then which of the following statements are true?

(a)

(b) If f is onto then the function f(cos z) is onto.

(d) If f is one-one then the function f(z⁴ + z + 2) is one-one.

Ans. (a), (b)

Sol.

49. Consider the entire functions f(z) = 1 + z + z²⁰ and g(z) = e^z, Which of the following statements are true?

(a)

(b)

(d) is bounded for every R > 0

Ans. (a), (c)

Sol.

50. Which of the following statements are true?

(a) tan z is an entire function.

(b) tan z is a meromorphic function on C.

(d) tan z has a non-isolated singularity at

Ans. (b), (d)

Sol.

51. Let a₁ < a₂ < ... < a₅₁ be given distinct natural numbers such that 1 ≤ a_i ≤ 100 for all i = 1, 2, ...., 51. Then which of the following are correct?

(a)

(b)

(c)

(d) There exist i < j such that |a_i – a_j| > 51.

Ans. (a), (b), (c)

Sol.

52. For any group G, let Aut(G) denote the group of automorphisms of G. Which of the following are true?

(a) If G is finite then Aut(G) is finite.

(b) If G is cyclic then Aut(G) is cyclic.

(d) If Aut(G) is isomorphic to Aut(H) where G and H are two groups, then G is isomorphic ot H.

Ans. (a)

Sol.

53. Let G be a group with the following property:

Given any positive integers m, n and r there exist elements g and k in G such that order (g) = m, order (h) = n and order (gh) = r. Then which of the following are necessarily true?

(a) G has to be an infinite group.

(b) G cannot be a cyclic group.

(d) G has to be a non-abelian group.

Ans. (a), (b), (c), (d)

Sol.

54. Let R be the ring C[x]/(x² + 1). Pick the correct statements from below:

(a) dim_CR = 3

(b) R has exactly two prime ideals

(d) (x) is a maximal ideal of R

Ans. (b)

Sol.

55. Let f(x) = x⁷ – 105x + 12. Then which of the following are correct?

(a) f(x is reducible over Q.

(b) There exists an integer m such that f(m) = 105.

(d) f(m) is not a prime number for any integer m.

Ans. (d)

Sol.

56.

Pick the correct statements from below:

(a)

(b)

(c)

(d)

Ans. (a), (b), (c), (d)

Sol.

57. Let with the metric Let f : x be the function defined by Choose the correct statements from below:

(a) f is continuous

(b) f is onto

(d) f is open

Ans. (a), (b)

Sol.

58. Let A be a subset of R satisfying where for each n > 1, V_n is an open dense subset of R. Which of the following are correct?

(a) A is non-empty set

(b) A is uncountable

(d) A is dense in R

Ans. (a), (b)

Sol.

59. Three solutions of a certain second order non-homogeneous linear differentiable equation are

Which of the following is/are general solution(s) of the differential equation?

(a) (C₁ + 1)y₁ + (C₂ – C₁)y₂ – C₂y₃ where C₁ and C₂ are arbitrary constants.

(b) C₁(y₁ – y₂) + C₂(y₂ – y₃) where C₁ and C₂ are arbitrary constants.

(d) C₁(y₁ – y₃) + C₂(y₃ – y₂) + y₁ where C₁ and C₂ are arbitrary constants.

Ans. (a), (d)

Sol.

60. The method of variation of parameters to solve the differential equation where and p(x), q(x), r(x) are non-zero continuous functions on an interval I, seeks a particular solution of the form y_p(x) = v₁(x)y₁(x) + v₂(x)y₂(x) where y₁ and y₂ are linearly independent solutions of and v₁(x) and v₂(x) are functions to be determined. Which of the following statements are necessarily true?

(a) The Wronskian of y₁ and y₂ is never zero in I.

(b) v₁, v₂ and v₁y₁ + v₂y₂ are twice differentiable.

(d) The solution set of consists of functions of the form ay₁ + by₂ + y_p where are arbitrary constants.

Ans. (a), (c), (d)

Sol.

61. Consider the eigenvalue problem

Which of the following statements are true?

(a) All eigenvalues are strictly positive.

(b) All eigenvalues are non-negative.

(d) The sequence of eigenvalues is bounded above.

Ans. (b), (c)

Sol.

62. Consider the IVP:

Then

(a) the solution is singular at (0, 0).

(b) the given space curve is not a characteristic curve at (0, 0).

(d) a necessary condition for the IVP to have a unique C¹ solution at (0, 0) does not hold.

Ans. (a), (b), (c), (d)

Sol.

63. Let u(x, t) be a function that satisfies the PDE : u_t + uu_x = 1, t > 0, and the initial condition Then the IVP has

(a) only one solution.

(b) two solutions.

(d) solutions none of which is differentiable on the characteristic base curve.

Ans. (b), (d)

Sol.

64. Let be twice continuously differentiable function with a unique fixed point (fx_*) = x_*. For given consider the iteration x_{n + 1} = f(x_n) for n ≥ 0.

(a) If L < 1, then x_n converges to x_*

(b)

(d) If f^t(x_*) = 0, then |e_{n + 1}| < C|e_n|² for some C > 0

Ans. (a), (c), (d)

Sol.

65. Let u(x) satisfy the boundary value problem

Consider the finite difference approximation to (BVP)

Here, U_j is an approximation to u(x_j) where x_j = jh, j = 0, ...., N is a partition of [0, 1] with h = 1/N for some positive integer N. Then which of the following are true?

(a) There exists a solution to (BVP)_h of the form U_j = ar^j + b for some and r satisfying (2 + h)r² – 4r + (2 – h) = 0.

(b) U_j = (r^j – 1)/(r^N – 1) where r satisfies (2 + h)r² – 4r + (2 – h) = 0 and

(d) U_j is monotonic is j.

Ans. (a), (b), (c), (d)

Sol.

66. Consider the functional subject to y(0) = 0, y(1) = 0. A broken extremal is a continuous extremal whose derivative has jump discontinuities at a finite number of points. Then which of the following statements are true?

(a) There are no broken extremals and y = 0 is an extremal.

(b) There is a unique broken extremal.

(d) There exist infinitely many broken extremals.

Ans. (c)

Sol.

67. The extremals of the functional

(a) x⁶ + 2x³ – 3x²

(b) x⁵ + 4x⁴ – 5x³

(d) x⁶ + 4x³ – 6x²

Ans. (a)

Sol.

68. If g is the solution of

(a) 2

(b) 4

(d) 8

Ans. (a)

Sol.

69. A characteristic number and the corresponding eigenfunction of the homogeneous Fredholm integral equation with kernel

are

(a)

(b)

(c)

(d)

Ans. (a), (d)

Sol.

70. Consider a point mass of mass m which is attached to a mass-less rigid rod of length a. The other end of the rod is made to move vertically such that its downward displacement from the origin at time t is given by The mass is moving in a fixed plane and its position vector at time t is given by